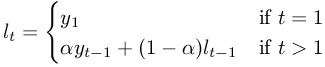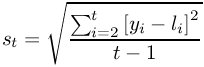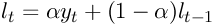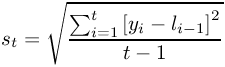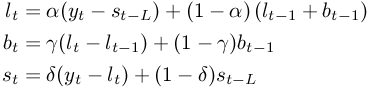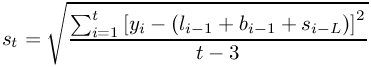The Gnumeric Manual, version 1.12
-
1. Welcome!
-
2. How to Use This Manual
-
3. A Quick Introduction
- 3.1. Working with Gnumeric
- 3.2. Starting Gnumeric the First Time
- 3.3. The Parts of Gnumeric
- 3.4. Using Commands
- 3.5. Data in Gnumeric
- 3.6. Cell Formats
- 3.7. Complex Cell Selections
- 3.8. Moving Cell Contents, Inserting New Cells or Deleting Cells
- 3.9. Sheets
- 3.10. Graphing
- 3.11. Printing
- 3.12. File Opening and Saving
- 3.13. Closing Gnumeric
-
4. Gnumeric Elements
- 4.1. Overview
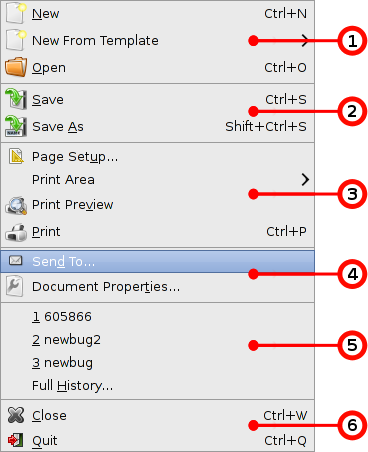
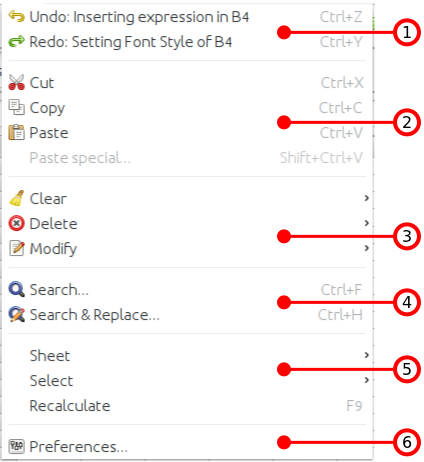
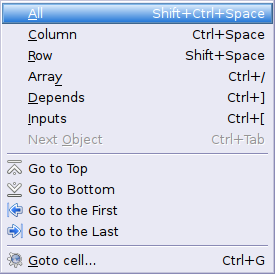
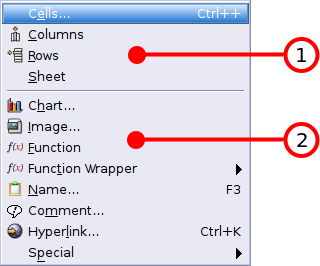
- 4.2. Menus
- 4.3. Context Menus
- 4.4. Toolbars
- 4.5. Data Entry Area
- 4.6. The Cell Grid
- 4.7. The Information Area
- 4.8. The Mouse Pointers used by Gnumeric
-
5. Working with Data
- 5.1. Data in Gnumeric Cells
- 5.2. The Types of Cell Elements
- 5.3. Data Entry
- 5.4. Advanced Data Entry
- 5.5. Obtaining Data from External Sources
- 5.6. Selecting Cells and Cell Ranges
- 5.7. Moving and Copying Data
- 5.8. Deleting Data
- 5.9. Inserting New Data Cells
- 5.10. Formatting Cells
- 5.11. Conditional Formatting of Cells
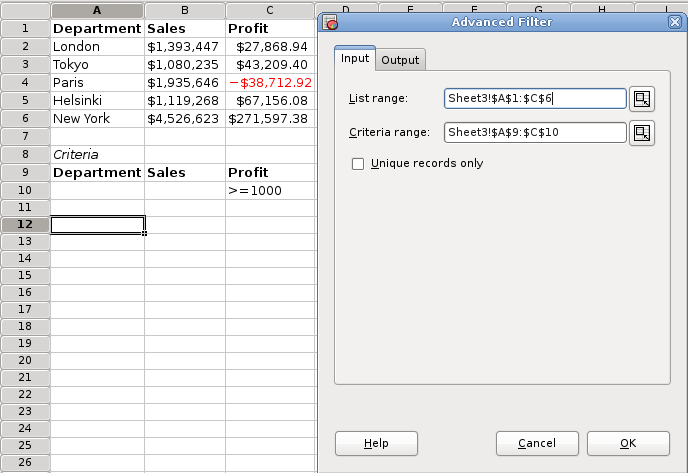
- 5.12. Filtering Data
- 5.13. Modifying Data
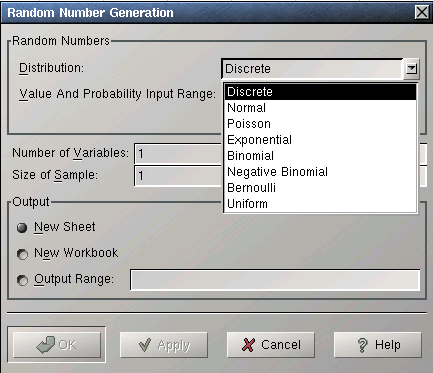
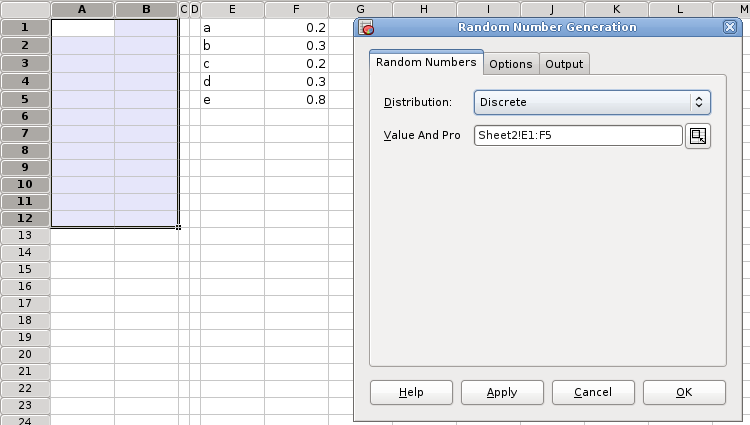
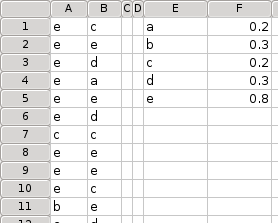
- 5.14. Generating Data
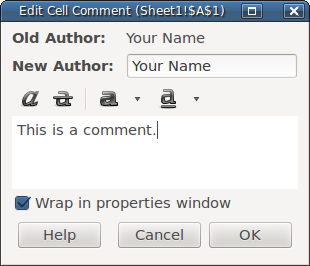
- 5.15. Comments in Cells
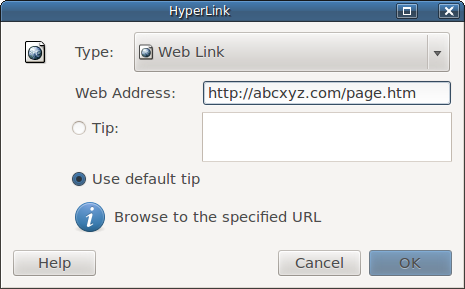
- 5.16. Hyperlinks
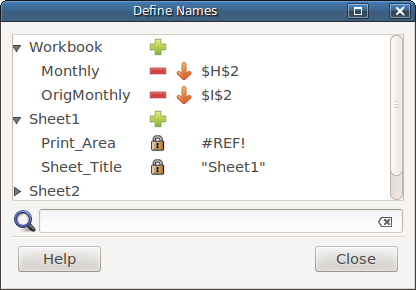
- 5.17. Defining Names
-
6. Advanced Analysis
- 6.1. Advanced Analysis in Gnumeric
- 6.2. Analysis using Complex Numbers
- 6.3. Goal Seek Tool
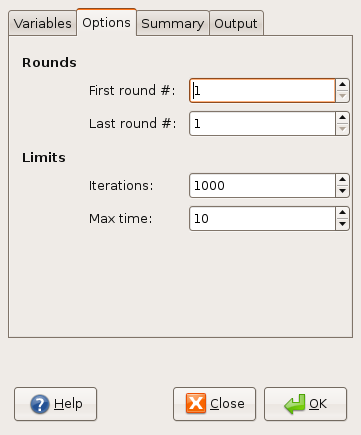
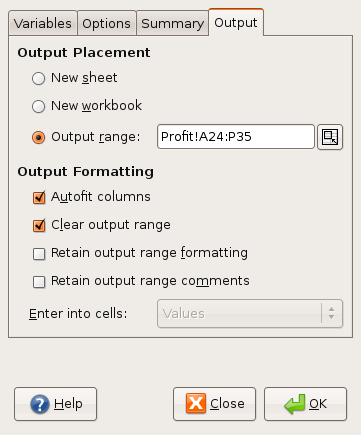
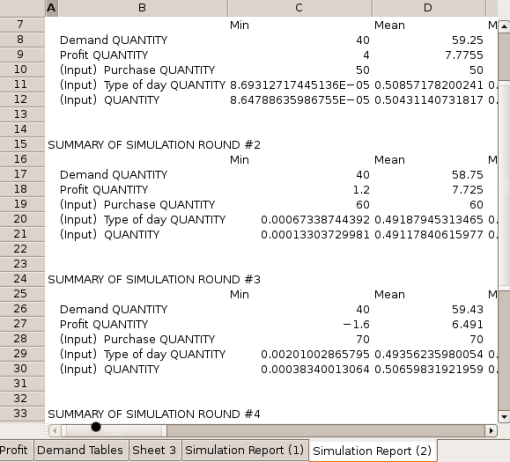
- 6.4. Simulation Analysis
- 6.5. Analysis using scenarios
-
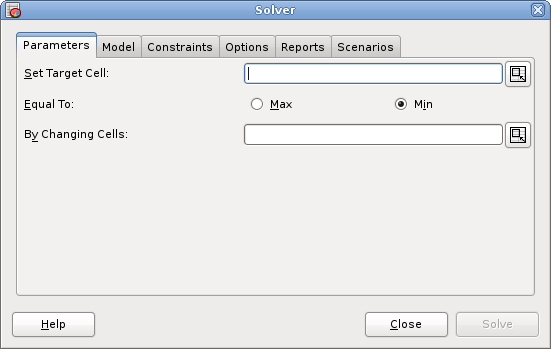
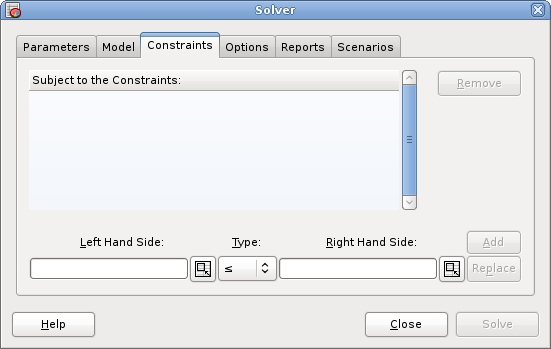
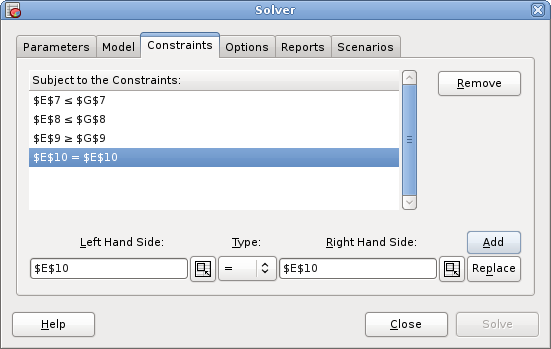
7. The Solver
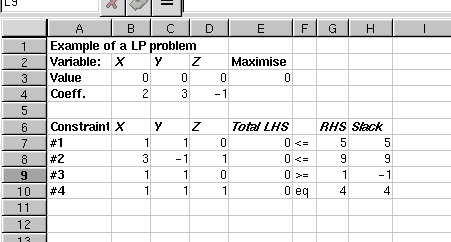
- 7.1. Solver
-
8. Statistical Analysis
- 8.1. Overview
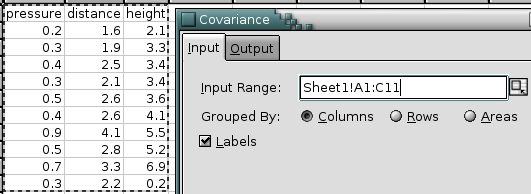
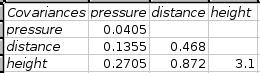
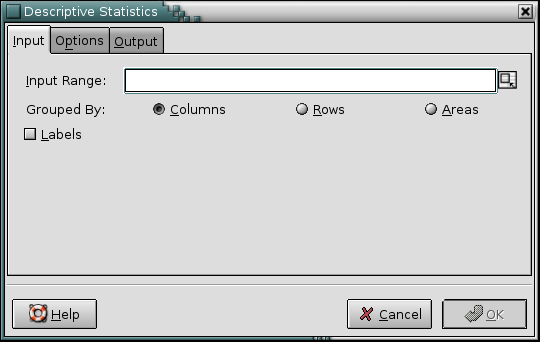
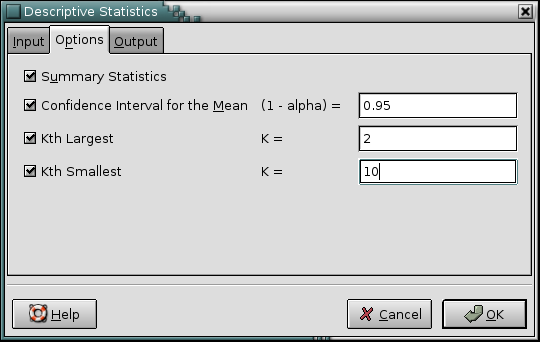
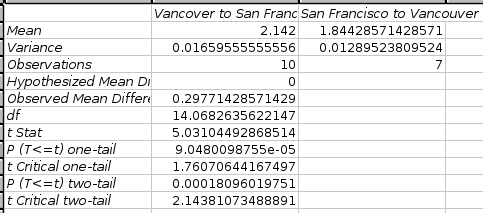
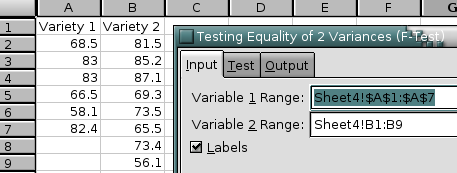
- 8.2. Descriptive Statistics
- 8.3. Sampling Tool
- 8.4. Dependent Observations
- 8.5. One Sample Tests
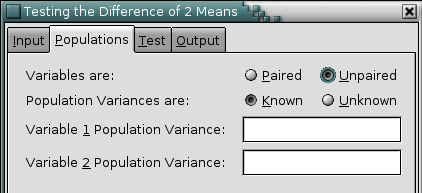
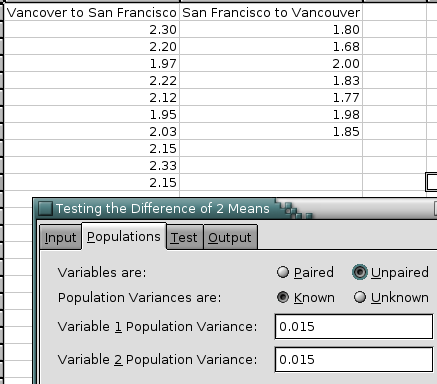
- 8.6. Two Sample Tests
- 8.7. Multiple Sample Tests
-
9. Graphics: Images, Widgets, and Drawings
- 9.1. Overview
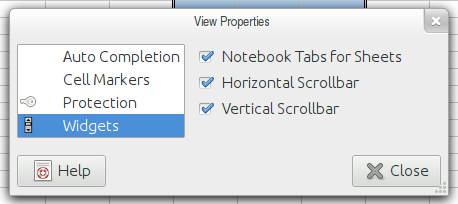
- 9.2. Images
- 9.3. GUI Widgets
- 9.4. Drawing Elements
-
10. Graphs
- 10.1. Overview of Graphs
- 10.2. The Graph Guru
- 10.3. Plot Types
- 10.4. Configuring Graph Element Properties
- 10.5. Pre-Selecting Data
-
11. Using Worksheets
- 11.1. Worksheet Overview
- 11.2. Worksheet Navigation
- 11.3. Worksheet Display
- 11.4. General Settings
- 11.5. Print Settings
- 11.6. Managing Worksheets
-
12. Workbook Settings
- 12.1. Overview
- 12.2. Document Summary
- 12.3. Document Settings
- 12.4. Document Named Elements
-
13. Configuring Gnumeric
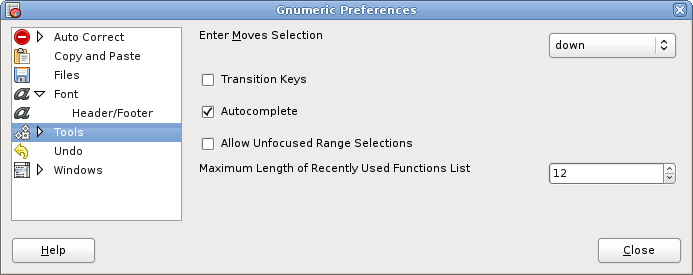
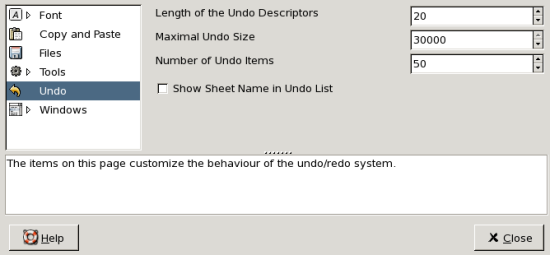
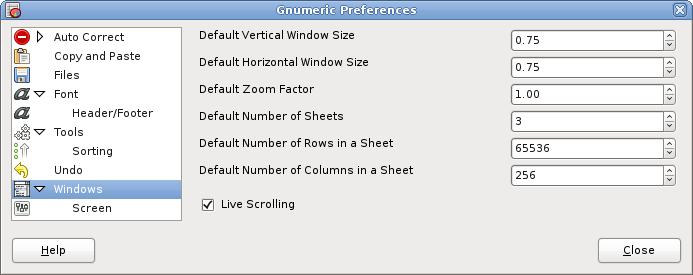
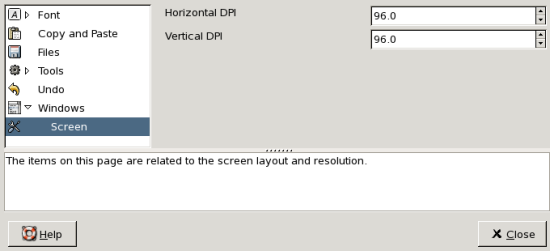
- 13.1. Overview
- 13.2. General Preferences
- 13.3. Toolbars
- 13.4. Plugins
- 13.5. Languages and Locales
-
14. Working with Files
- 14.1. Files in Gnumeric
- 14.2. File Formats
- 14.3. Opening Files
- 14.4. Importing Text Files
- 14.5. Saving Files
- 14.6. Exporting Text Files
- 14.7. Sending Files
- 14.8. Converting Files
-
15. Printing
- 15.1. Printing to a Printer or a File.
- 15.2. Page Setup.
- 15.3. Print Preview
-
16. Getting More Help
- 16.1. Sources of Help
- 16.2. Web Resources
- 16.3. Related Manuals
- 16.4. The Mailing List
- 16.5. Internet Chat (IRC)
-
17. Reporting a Problem
- 17.1. Overview
- 17.2. Defining the error
- 17.3. Opening an account
- 17.4. Filing a report
- 18. Extending Gnumeric
-
A. Function Reference
- A.1. Bitwise Operations
- A.2. Complex
- A.3. Database
- A.4. Date/Time
- A.5. Engineering
- A.6. Erlang
- A.7. Finance
- A.8. Gnumeric
- A.9. Information
- A.10. Logic
- A.11. Lookup
- A.12. Mathematics
- A.13. Number Theory
- A.14. Random Numbers
- A.15. Statistics
- A.16. String
- A.17. Time Series Analysis
-
B. Keybinding Reference
1. Welcome!
Gnumeric is a spreadsheet, a computer program used to manipulate and analyze numeric data. Gnumeric can help you keep track of information in lists, organize numeric values in columns and rows, perform and update complex calculations by defining each step of the calculation and modifying particular steps subsequently, create and display or print graphical plots of data using bar plots, line graphs, pie charts or radar charts, implement complex optimization modeling or perform many other tasks involving numbers, dates, times, names or other data.
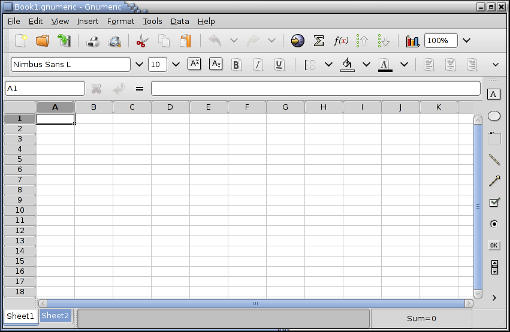
The features of Gnumeric make it versatile and powerful. The screenshot (picture) of Gnumeric shown in Figure 1-1 demonstrates the main program window and some of the features currently available.
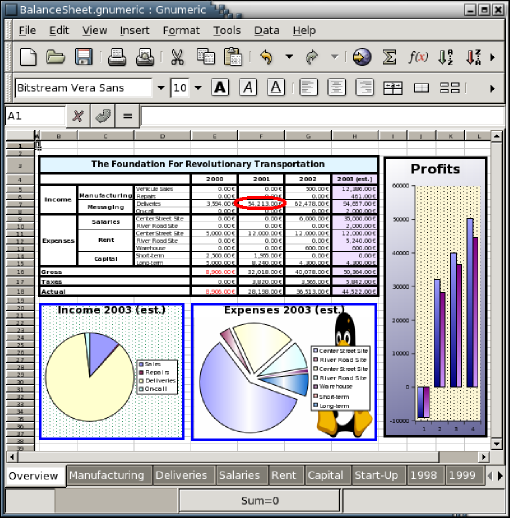
An example of Gnumeric, shrunk to fit in this document.
Gnumeric aims to be the best spreadsheet available. It has been developed over many years to become mature and mathematically correct. Gnumeric was created and is maintained by the GNOME project. This manual describes version 1.12 of Gnumeric.
Releases of Gnumeric in the 1.12 series have numbers starting with 1.12 but with extra numbers afterwards, such as 1.12.0 or 1.12.3. These are stable releases which are only changed with minor improvements and fixes for problems (bugs) in the program. These releases can be considered safe for use in a production environment.
The 1.13 series of releases are unstable releases meant for developer testing. If you want a stable release get the most recent release from the 1.12 series.
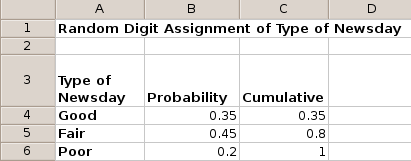
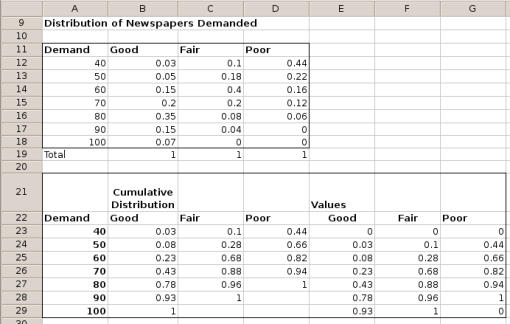
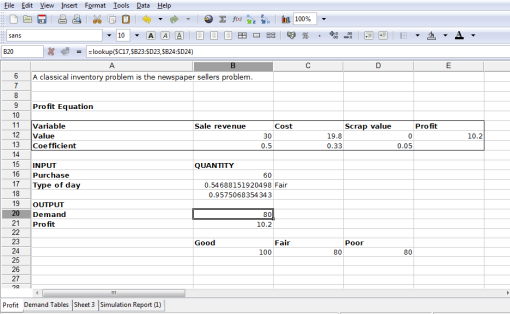
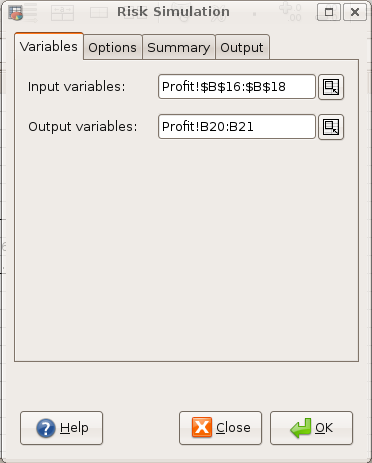
Goals of Gnumeric
Gnumeric is developed with a specific set of goals in mind.
-
Stability
Gnumeric has undergone significant amounts of testing. A diverse group of users evaluates Gnumeric in a wide variety of environments. Testing workbooks are used to assess the mathematical correctness of the calculations and to validate the quality of the file importers.
-
Accuracy
Calculating the correct answer is important, and Gnumeric has worked hard to surpass the competition. Recent reports indicate that it has done so.
-
File compatibility
Transparent access and manipulation of files from other applications is vital in a modern office. The Gnumeric file format is simply compressed XML which can be decompressed using gunzip, the GNU gzip program's decompression utility, into text. Gnumeric can open files from several well known proprietary and free spreadsheets including MS Excel™, Lotus 1-2-3™, Applix™, OpenOffice.org™, Psion™, Sylk™, XBase™, Oleo™, PlanPerfect™, Quattro Pro™ and HTML. Gnumeric can save files to several versions of the MS Excel™ file format and can save tables into LaTeX \longtable, HTML, and roff files. Gnumeric also benefits from a highly configurable text importer and exporter which ensures that data can be transferred smoothly, and allows new formats to be added easily as plug-in software routines.
-
Minimal cost of transition
Learning new and unfamiliar interfaces is an expensive and frustrating process. Gnumeric attempts to present itself so that a user's familiarity with other applications will still apply and to offer new features in an intuitive manner.
-
Extensive feature set
Gnumeric now has enough of the features that users expect in a spreadsheet to provide for the vast majority of user needs. However, new features are constantly being added. People often quote the statistic that most users only need 20% of the features of the software they use. This statistic does not mean that only 20% of the features are needed but, rather, that most users share a common need for 10% of the features and require distinct features for the rest of their work. Gnumeric attempts to provide full implementations of the features it offers, leaving features unimplemented until a robust and complete implementation exists.
-
Internationalization
Gnumeric has been translated into 46 languages, and is being used by people around the globe with the symbols and date/monetary conventions appropriate for their local setting.
-
Scalability
The core architecture is designed to ensure that Gnumeric can comfortably scale to moderately large loads (1 million cells) while remaining usable on older hardware.
-
Openness
Gnumeric is free software in the sense of giving its users several freedoms related to the program including the freedoms to use, modify and redistribute the program. These freedoms are explained at the Free Software Foundation web site page on the philosophy of free software. In order to maintain these freedoms for everyone, certain restrictions are required which prevent anyone limiting these freedom for others. Gnumeric is therefore released under a particular license agreement; Gnumeric is licensed under the terms of the GNU GPL.
One of the consequences of these freedoms, is that everyone can have access to the source code used to create Gnumeric. This code is explicitly maintained and documented to make it easy for anyone to modify in any way they choose. This makes it possible to modify the spreadsheet, write custom routines or extend Gnumeric for special needs.
The Gnumeric 1.13 Series of Releases for Developers
The Gnumeric 1.13 series of releases are developer releases. These releases are kept as stable as possible. However, each release in this series includes changes and improvements some of which may be quite large. These new changes may cause the program to crash and lose data. Do not use these releases if you cannot afford to lose any data or work. However, these releases include many new features that can be helpful. If you use this series, backup your data often, not just by saving files but by renaming them and checking that they can be reopened. If you experience mistakes or crashes while you are using this version, please report these using the GNOME project's bug reporting interface as detailed in Chapter 17 ― Reporting a Problem.
New features introduced in the Gnumeric 1.12 release series:
The 1.12 series of Gnumeric is primarily a port of Gnumeric to version 3 of the GTK library. It alos includes some other improvements over the versions in the 1.10 series.
-
Improved OpenDocument Format (ODF) support
Both ODF import and export have been improved.
New features introduced in the Gnumeric 1.10 release series:
The 1.10 series of Gnumeric includes numerous improvements over the versions in the 1.8 series.
-
Adjustable Sheet Size
Sheets are no longer restricted to 256 columns of 65536 rows.
-
Improved OpenDocument Format Import and Export
Basic import and export support for the OpenDocument Format ("ODF") format was added, focussing on standard spreadsheet content and charts. Gnumeric also supports nearly all functions in the large group of functions in the current OpenFormula Draft.
-
Improved Microsoft OfficeOpenXML import and export
Import and export of Office Open XML ("OOXML") format files was significantly improved.
-
New and Improved Graphs
New plot types for surfaces and probability plots have been added. Moreover, when an axis is a date or time axis, reasonable places for tick marks will now be picked. Trend lines have also been improved
-
Conditional Formatting
Gnumeric now supports conditional formatting of cells. Gnumeric's conditional formatting supports an arbitrary number of conditions.
-
Faster Evaluation
Evaluation of some fairly common sheets with large numbers of calls to HLOOKUP, or similar functions, over the same database have been improved from “rather slow” to “instant”. Similar improvements have been implemented for farms of RANK or PERCENTILE calls.
-
Reduced Memory Usage
The memory usage for large sheets has been decreased significantly.
-
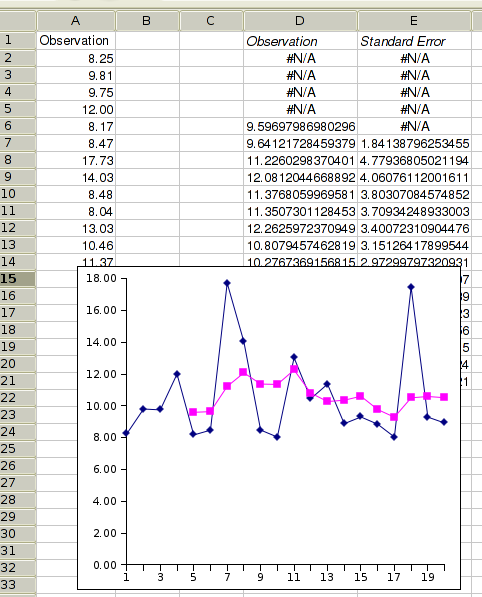
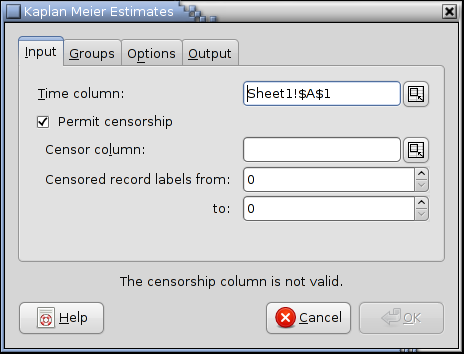
Added Statistical Analysis Tools
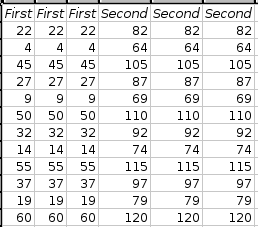
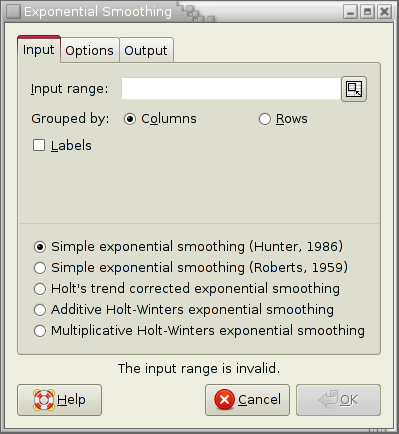
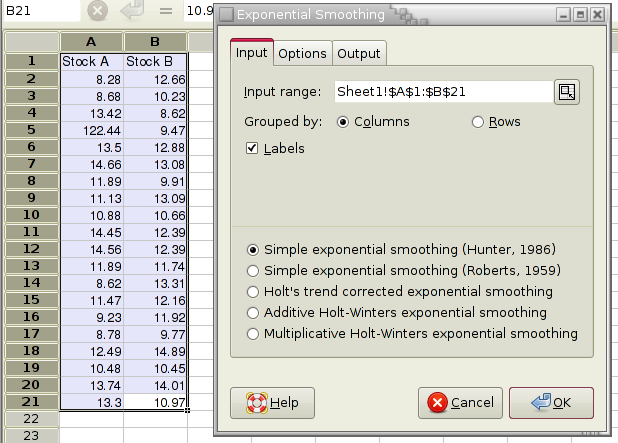
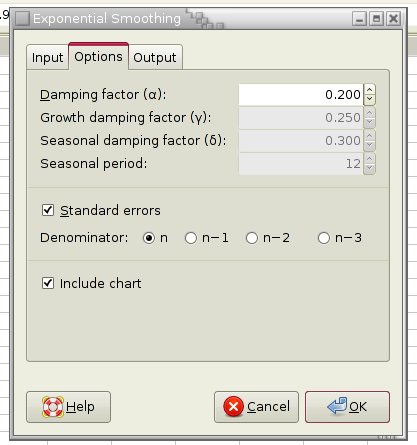
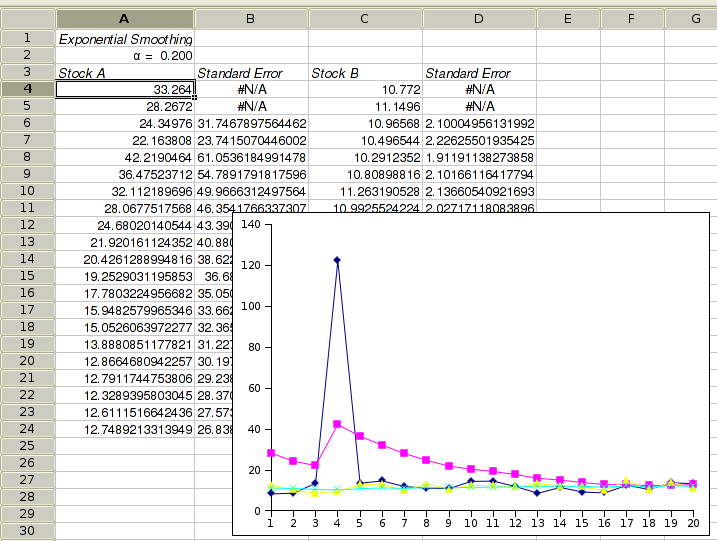
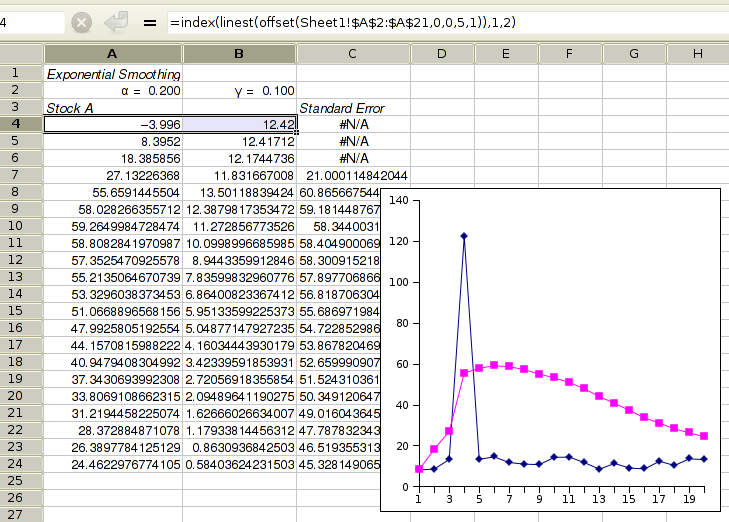
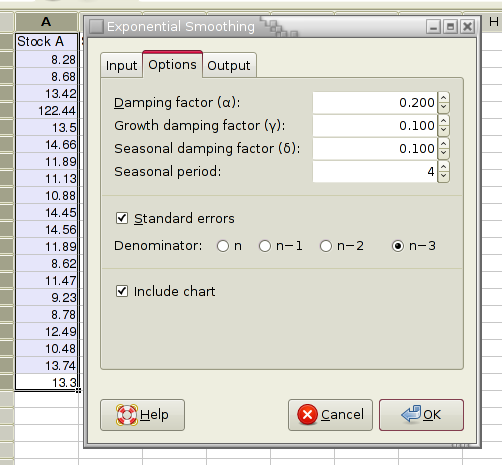
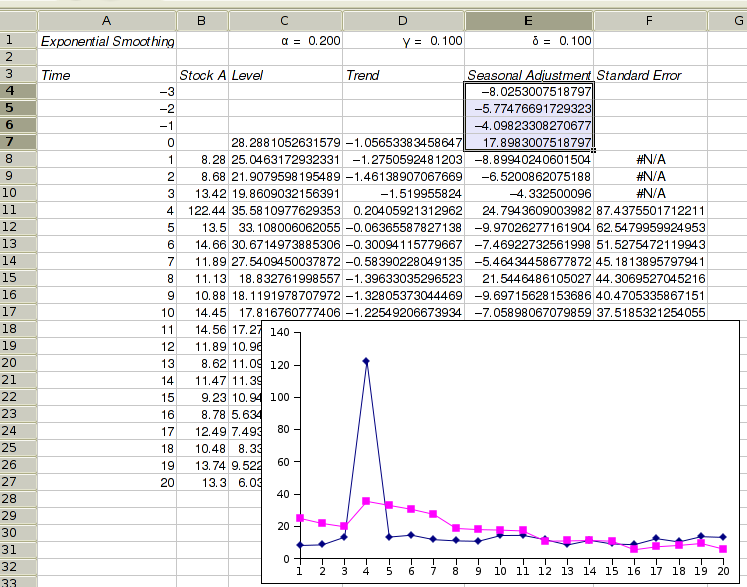
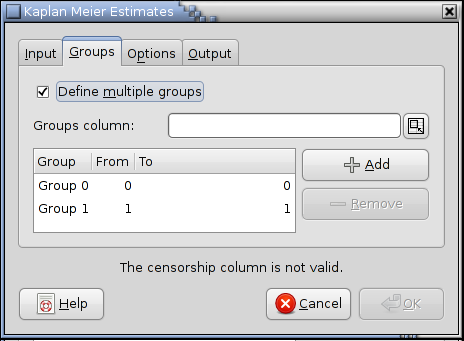
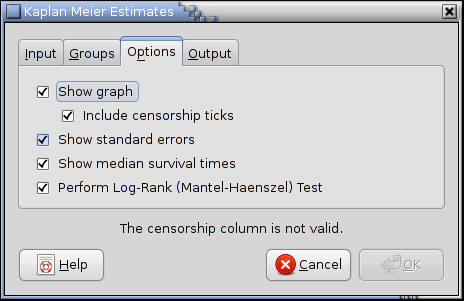
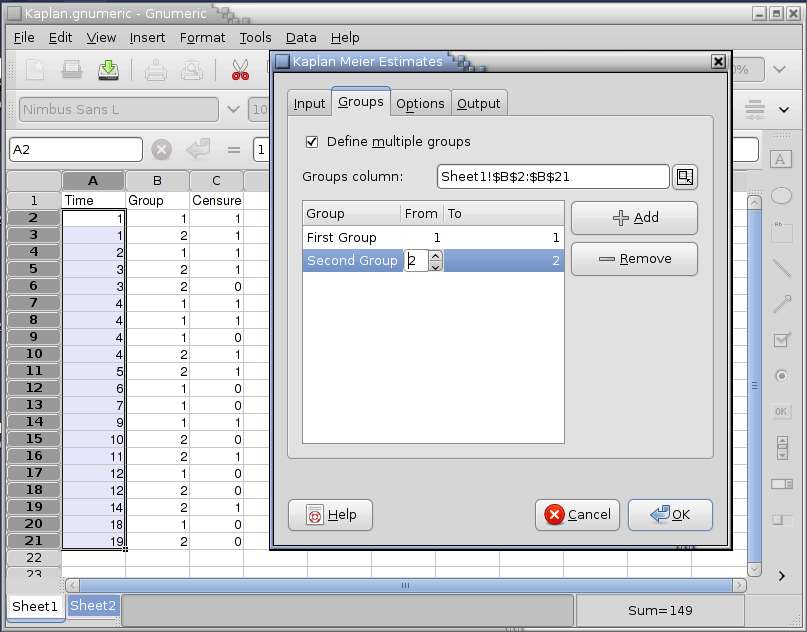
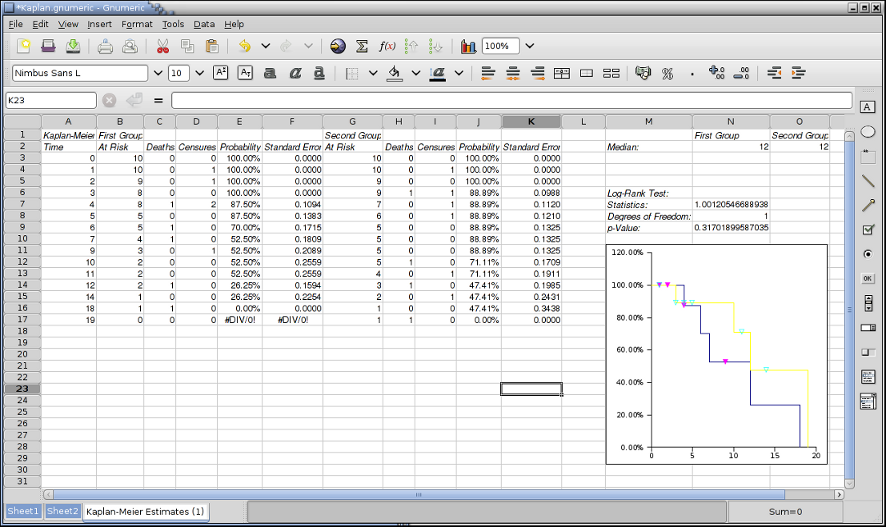
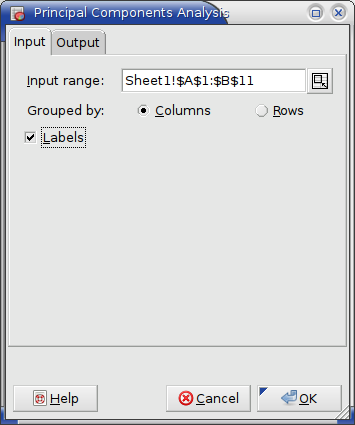
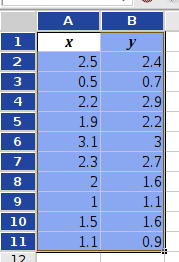
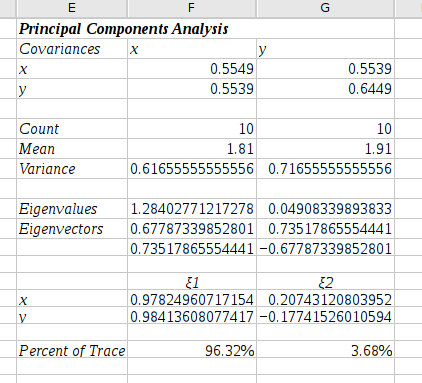
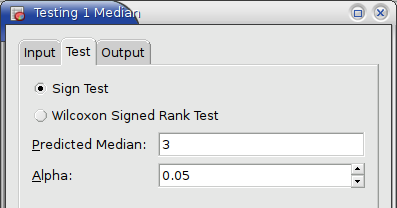
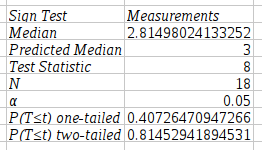
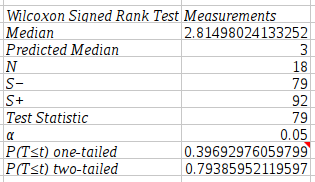
The statistical analysis tools have been improved and there are quite a few new ones, for example Kaplan Meier Estimates, Normality Tests, Principal Component Analysis, Sign Tests, improved Exponential Smoothing, various basic non-parametric tests, etc.
-
Improved Sheet Objects
Support for sheet objects (lines, arrows, widgets, …) has been improved.
New features introduced in the Gnumeric 1.8 release series:
The 1.8 series of Gnumeric includes numerous improvements over the versions in the 1.6 series.
-
Improved .gnumeric and export
Gnumeric now uses the faster SAX based parser by default for parsing .gnumeric files. The schema was improved and additional features were added.
-
Microsoft OfficeOpenXML import and export
Basic import and export support for the Office Open XML ("OOXML") format was added, focussing on standard spreadsheet content. Charts and embedded objects are not yet supported.
-
New value formatting engine
Improved compatibility and performance.
-
Use new Gtk based Printing
The printing infrastructure was changed to use Gtk based printing instead of the deprecated libgnomeprint libraries.
-
Improved in-cell drop downs
In cell validation lists, and improved finger feel for autofilters.
New features introduced in the Gnumeric 1.6 release series:
The 1.6 series of Gnumeric included numerous improvements over the versions in the 1.4 series.
-
Better Charting:
Several new types of charts have been added, and many features, such as regression lines, have been added.
-
Improved Accuracy:
While Gnumeric 1.4 was already the best available source for accuracy in statistical calculations, Gnumeric 1.6 is even better. We are continuing our behind-the-scenes cooperation with The R Project to make this happen. We have also added a new plugin supplying consistently named probability density, cumulative density, and reverse cumulative density functions to Gnumeric. The new function names mirror their R counterparts.
-
The Port to Microsoft Operating Systems
Our "Windows" port is now mature enough for everyday use. We have improved the theming support of our custom widgets, so Gnumeric now looks and feels slightly more like a native application. The build might still have a few rough edges, but those are being worked on.
-
Right-to-Left Support:
We now support right-to-left orientation of the sheets as well as for text within cells.
New features introduced in the Gnumeric 1.4 release series:
The 1.4 series of Gnumeric included numerous improvements over the versions in the 1.2 series.
-
The Port to Microsoft Operating Systems
The port of the core of Gnumeric to the GTK+ libraries will enable the application to be run on the series of operating systems sold by Microsoft and colloquially known as "Windows".
-
Improved Analytics
The analytical correctness of Gnumeric is a primary concern of the team. The precision and correctness of the analytics are constantly being evaluated and improved. Updated versions of the solver libraries (lp_solve and GLPK) were added.
-
Improved Charting
The graphical system is improving rapidly with new types of graphs, such as radar plots. There is now support for error bars and additional styles. The plots also look significantly sharper on screen, and off thanks to some pixel tuning. The axes now support various mappings (logarithmic, inverse), and there are a wider selection of markers. There is also support for formatting individual points in a plot.
-
Rich Text In Cells
The ability to use Rich Text has been added in this version. This allows a single cell to contain text with mixed formatting including bold, italic and other formats.
-
Improved Microsoft Excel Compatibility
The file format used by the Microsoft Excel™ spreadsheet is commonly used to exchange spreadsheet documents. The Gnumeric team spends a considerable effort reverse engineering that file format to ensure that Gnumeric can read and write files in that format. This release now supports all forms of 'array formula' and adds export support for charts, rich text, and images. More compatibility accelerator keys were added to simplify transition, and improve the finger feel. There is better support for hyperlinks.
-
Printing
Using Pango throughout the printing subsystem improves the consistency between on screen and resulting paper.
-
Improved Analytics:
This version of Gnumeric includes 470 sheet functions including all of the functions from the North American edition of Microsoft Excel 2000 (TM). This version also includes numerous new functions and statistical routines imported from the R statistical language, from the GNU Scientific Library, and from other sources. The random number generation has been updated to include Beta, Cauchy, Chi-Squared, Exponential power F, Gamma, Geometric, Laplace, Levy alpha-Stable Logarithmic, Logistic, Log-normal, Pareto, Rayleigh Rayleigh tail, T, Type I Gumbel, Type II Gumbel, Weibull Gaussian Tail, Landau, and Uniform integer distributions. The derivative valuation routines have been expanded to include Black-Scholes (and sensitivities), Garman Kohlhagen, Merton Jump Diffusion process, Bjerksund and Stensland (American options), Forward Starts, Simple and Complex Choosers, Exchange Options, options on future spreads, and most favourable state payouts. The solver has been improved with new linear and quadratic programming routines. There were improvements in the T-Test, Z-Test, and F-Test. More accuracy for GEOMDIST, BINOMDIST, BETADIST, BETAINV, FINV, CAUCHY, FDIST, FTEST, HYPGEOMDIST, ERF, FISHER, EFFECT, NOMINAL, MIRR, IRR, XNPV, NPV, PMT, RATE, PV, FV, IPMT, PPMT, ZTEST, EXPM1, LN1P.
-
Import/Export
The xml exporter is now much faster and lighter for .gnumeric files, and the GNOME enabled Gnumeric supports gnome-vfs and drag-n-drop images and files.
-
GTK+ Port
One of the principal aims of this developers series is to make Gnumeric work using only the GTK+ libraries. These libraries, following their 2.4.0 release, have all the functionality needed for the core of Gnumeric. This work will remove all dependencies in the core code on GNOME libraries although a version with the more complete features included in GNOME will still exist.
The 1.4.x release is dedicated to the memory of lost colleagues, Chema (Grandma) Celorio who helped make Gnumeric as stable as it is, and Mel Seder who kept us smiling. They'll be missed.
For more details on the changes in Gnumeric, refer to the file; named NEWS in the source code distribution.
Known Issues in Gnumeric:
The current list of all known and reported problems with Gnumeric is maintained in the GNOME bugzilla database. This list can be accessed using this bugzilla query.
2. How to Use This Manual
There are several ways to use this manual depending on what kind of user you are.
-
New users
If you are new to computers or to spreadsheets consider reading Chapter 3 ― A Quick Introduction, titled "A Quick Introduction", which explains the basics of spreadsheets in general and Gnumeric in particular.
-
Users who want specific help
Quickly finding help for a particular question can be quite hard. We suggest first reading the explanations of the contents of each chapter which are given below to try to figure out where your question might be answered, and then go directly to that section.
The chapters of this version of the Gnumeric manual are organized as follows:
-
Chapter 3 ― A Quick Introduction: A Quick Introduction
The best way to learn how to use Gnumeric is to begin exploring the program yourself. This chapter will help you get started trying new things and seeing what happens. The chapter explains the fundamentals of spreadsheets in general and of Gnumeric in particular. The chapter attempts to help new users get started with Gnumeric and provides background for the more detailed explanations given in the rest of the manual.
-
Chapter 4 ― Gnumeric Elements: Gnumeric Elements
This chapter describes all of the pieces of Gnumeric which a user can manipulate. The chapter provides explanations for each of the menus, menu entries, toolbar buttons and other elements of the graphical user interface.
-
Chapter 5 ― Working with Data: Working with Data
This chapter explains the core functionality of Gnumeric including the basic types of data manipulated by Gnumeric, the methods of entering, altering and formatting data, and the basic tools for analysis of these data. More advanced analysis is described in Chapter 6 ― Advanced Analysis.
-
Chapter 6 ― Advanced Analysis: Advanced Analysis
This chapter explains the advanced analytic tools available in Gnumeric including linear algebra calculations, the goal seek tool, simulation analysis, and scenarios.
-
Chapter 7 ― The Solver: The Solver
This chapter explains how to use Gnumeric's linear programming Solver.
-
Chapter 8 ― Statistical Analysis: Statistical Analysis
This chapter explains the various statistical analysis tools available in Gnumeric including tools to create descriptive statistics, as well as parametric and non-parametric hypotheses tests.
-
Chapter 9 ― Graphics: Images, Widgets, and Drawings: Graphics: Images, Widgets, and Drawings
This chapter explains how to add graphical elements to a Gnumeric worksheet, including images from external files, graphical user interface widgets which interact with worksheet data, and simple drawing elements.
-
Chapter 10 ― Graphs: Graphs
This chapter explains how to add data graphs to a Gnumeric worksheet, that can be used to plot worksheet data.
-
Chapter 11 ― Using Worksheets: Using Worksheets
This chapter explains the use and manipulation of worksheets in Gnumeric. The chapter explains how to move around a worksheet, how to alter the appearance and display organization of the worksheet contents, how to manipulate entire worksheets and how to protect worksheet contents.
-
Chapter 12 ― Workbook Settings: Workbook Settings
This chapter explains the contents of a Gnumeric workbook which are not part of the worksheets. This includes several settings which apply to the workbook and are saved in the Gnumeric file. Settings which apply to the Gnumeric program itself are called `preferences' and are explained in Chapter 13 ― Configuring Gnumeric.
-
Chapter 13 ― Configuring Gnumeric: Configuring Gnumeric
This chapter explains how to change the default behaviour of Gnumeric including the startup behaviour and default locale (language and number display).
-
Chapter 14 ― Working with Files: Working with Files
This chapter explains how to use files in Gnumeric. The chapter provides an extensive description of the file formats used by Gnumeric. The chapter also explains how to open files, import data from text files, save files, export data to text files, send data to others via electronic mail, and convert files from one format to another.
-
Chapter 15 ― Printing: Printing
This chapter explains how to print spreadsheets, tables and plots from Gnumeric to a printer directly or into PostScript or PDF (both are page description languages).
-
Chapter 16 ― Getting More Help: Getting More Help
This chapter describes other sources of help which are available to users including the Gnumeric web site, the mailing list, and the internet relay chat (IRC) discussion channel. The chapter also explains how to tell the project about a problem with the program.
-
Chapter 17 ― Reporting a Problem: Reporting a Problem
This chapter explains how to report a problem with Gnumeric so that the problem can be fixed. The same procedure can be used to file a report requesting an enhancement or a new feature.
-
Chapter 18 ― Extending Gnumeric: Extending Gnumeric
This chapter explains how to go about extending Gnumeric to provide extra functionality. Because Gnumeric is Free Software this is quite easy to do.
-
Appendix A ― Function Reference: Function Reference
This appendix provides a list of all the functions which are currently defined in Gnumeric.
-
Appendix B ― Keybinding Reference: Keybinding Reference
This appendix lists the keyboard shortcuts which are defined by default in Gnumeric.
3. A Quick Introduction
The best way to learn how to use Gnumeric is to begin exploring the program yourself. This chapter will help you get started trying new things and seeing what happens. The chapter explains the fundamentals of spreadsheets in general and of Gnumeric in particular. The chapter attempts to help new users get started with Gnumeric and provides background for the more detailed explanations given in the rest of the manual.
Getting started with computers
Unfortunately, this manual cannot teach you the very basics of interacting with a modern computer. If you have never used computers, don't know the names of the hardware components (the pieces you can touch) or don't know the names of the elements you see on the screen (like windows or the mouse pointer), you will probably want to get some basic advice from someone you know or read the manuals which came with your machine or your operating system. It's all pretty easy but, in order to understand this manual, you will need to know some basic terminology and have some basic computing skills.
If you are using the GNOME desktop environment, you can read the the GNOME Desktop User Guide for help in getting started with computers.
If you are using the another desktop environment such as KDE or another operating system, please see the instructions from the web site linked with either your desktop environment, your operating system, your software distribution source or the people who provided you with your computer. There are also many books providing good introduction to computers.
- 3.1. Working with Gnumeric
- 3.2. Starting Gnumeric the First Time
- 3.3. The Parts of Gnumeric
- 3.4. Using Commands
- 3.5. Data in Gnumeric
- 3.6. Cell Formats
- 3.7. Complex Cell Selections
- 3.8. Moving Cell Contents, Inserting New Cells or Deleting Cells
- 3.9. Sheets
- 3.10. Graphing
- 3.11. Printing
- 3.12. File Opening and Saving
- 3.13. Closing Gnumeric
3.1. Working with Gnumeric
Using a spreadsheet generally involves several steps. First the application is started to obtain an empty workbook, which generally has several empty worksheets. Next, data and formulas are entered into one or several sheets. The data may be entered by hand or imported from external files. The formulas are generally entered by hand, possibly with the help of various tools. The data may be formatted to appear in particular ways and to clarify the structure of the data in the worksheet. A user may also create several graphical plots. Certain parts of the spreadsheets may be printed out as tables. The work is then usually saved into a file which can be re-opened later to add or modify the contents of the workbook.
A spreadsheet file contains a workbook and possibly some other information about the file. Because a spreadsheet file contains exactly one workbook, the files themselves are often called workbooks. A workbook contains one or more worksheets. A worksheet consists of a number of cells, usually arranged in a two dimensional grid made up of columns and rows. We introduce the names of the parts of Gnumeric in Section 3.3 ― The Parts of Gnumeric and explain the parts further in Chapter 4 ― Gnumeric Elements.
3.2. Starting Gnumeric the First Time
Gnumeric can be started in several ways, depending on your computer operating system and desktop environment. The approaches described below are equivalent; they result in a Gnumeric window appearing on your monitor as shown below.
We assume that Gnumeric is already installed on your machine. Installing Gnumeric depends on the particular operating system and distribution used on your machine and is therefore beyond the scope of this manual. If Gnumeric is not already installed on your machine, read the manuals that came with your distribution or look at your distribution vendor's web site.
3.2.1. Starting Gnumeric from the GNOME desktop
If you are a GNOME user, you should have a ‘panel’ somewhere on your desktop. This panel contains icons and at least two menus. One of these menus is called and has an icon which looks like the outline of a foot. If you click on this menu name, a menu will appear. Drag the cursor down to the sub-menu name, and a sub-menu will appear. Drag the cursor into the sub-menu and then release the mouse button when the cursor is on the entry which reads "Gnumeric Spreadsheet." This will start the program and the main window of Gnumeric will appear as shown in Figure 3-1.
3.2.2. Starting Gnumeric from another *NIX desktop
If you run a UNIX-like operating system (called *NIX in this
manual) such as GNU/Linux, GNU on some other kernel, or a
commercial UNIX (TM) system, or if you use a commercially
distributed version of GNOME, KDE (K Desktop
Environment), or a similar desktop system, you will have to
find a way to launch Gnumeric
yourself. Hunt around the menus until you find something named
"Gnumeric", possibly with the
![]() icon, and then click on that menu entry.
icon, and then click on that menu entry.
On UNIX-like operating systems, Gnumeric requires the X window system to run.
3.2.3. Starting Gnumeric from a *NIX terminal
You can also start Gnumeric from the command line in an xterm window or equivalent terminal emulator. Open a terminal. At the shell prompt type:
gnumeric &
On UNIX-like operating systems, you must be running the X window system to run Gnumeric.
3.2.4. Starting Gnumeric from a Microsoft desktop
Gnumeric, starting with the 1.4 series, can be run as a native application on the Microsoft Windows operating systems. On those operating systems, The Start menu should contain an entry which will launch Gnumeric. The actual location of the menu item depends on the choices made during installation.
3.2.4.1. Starting Gnumeric from a Microsoft command prompt
You can also start Gnumeric from a shell window by finding the directory with the program itself which will be called gnumeric.exe. You can either move to that directory and type:
gnumeric
c:\Program Files\Gnome-Office\gnumeric
3.2.5. Starting from a Spreadsheet file
Gnumeric can also be opened using a spreadsheet file directly. If there is a spreadsheet file on the desktop or in a file manager like Nautilus, it may be possible to click or double-click with the mouse pointer on the file and have Gnumeric open the file automatically. Alternatively, you may be able to right click on the file and get a pop-up menu that will allow you to select Gnumeric as the application to use to open the file.
3.3. The Parts of Gnumeric
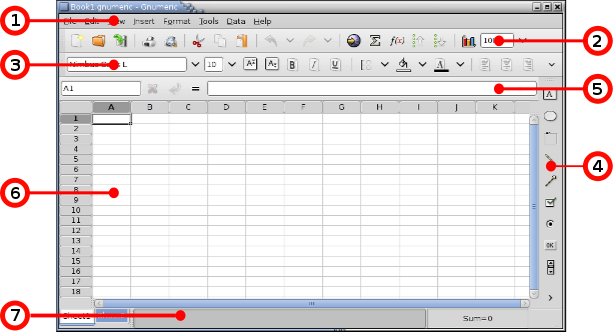
After opening, Gnumeric appears as was shown in Figure 3-1 but is shown below with the major components labeled. The open application contains a menubar at the top, two toolbars below the menu bar, and below these, on the left, the object toolbar, and, on the right, the data entry area above the cell grid area which itself is above the list of worksheets and the information area.
The part names are listed below along with a reference to the section that discusses that element. If you are reading this document on a computer, you may be able to click on a reference to jump to that section of the manual.
- 1 The menubar
-
The menubar provides access to the core functions of GNOME. Almost everything that you can do in Gnumeric you can do through the menus. We discuss the menus and menubar in Section 4.2 ― Menus.
- 2 The standard toolbar
-
The standard toolbar provides shortcuts for the most used items in the menus. We discuss the toolbars in Section 4.4 ― Toolbars and this toolbar in particular in Section 4.4.2 ― The Standard Toolbar.
- 3 The format toolbar
-
The format toolbar changes the display properties of data in the workbook. We present it in Section 4.4.3 ― The Format Toolbar, part of the general discussion of toolbars in Section 4.4 ― Toolbars.
- 4 The object toolbar
-
This toolbar enables you to draw graphic elements on the sheet, such as text labels, big red circles or thin green arrows. You can use these to bring attention to a particular part of a worksheet. We explain the object toolbar in Section 4.4.5 ― The Object Toolbar in the Section 4.4 ― Toolbars portion of this manual.
- 5 The data entry area
-
The data entry area is useful for the modification of complex formulas. We discuss it in Section 4.5 ― Data Entry Area.
- 6 The cell grid area
-
The cell area lies in the middle of all the rest. The cell area includes the row and column labels, the scrollbars and the tabs below. We explain the use of these elements in Section 4.6 ― The Cell Grid.
- 7 The information area
-
This area is used by Gnumeric to give you feedback on the status of certain operations. We explain this information in Section 4.7 ― The Information Area.
For a detailed explanation of each of these elements, see Section 4.1 ― Overview.
By default, Gnumeric opens a workbook with three worksheets and a file name of Book1.gnumeric.
3.4. Using Commands
You can access the commands provided by Gnumeric using several methods. These methods are explained here. The most important commands are explained in the rest of this chapter. We explain all of the commands in later chapters of this manual.
- 3.4.1. Using Menu Commands
- 3.4.2. Using Toolbar Button Commands
- 3.4.3. Using Context Menu Commands
- 3.4.4. Using Keyboard Shortcut Commands
3.4.1. Using Menu Commands
The menus provide the simplest way for you to get to all of the commands provided by Gnumeric. These menus work like those in any GNOME application: you click on the menu to open it, you drag the mouse cursor onto the menu and then release the mouse button (or click again) while the cursor is above a menu entry to execute that command. For further information, see Section 4.2 ― Menus.
3.4.2. Using Toolbar Button Commands
The buttons on the toolbars are quite simple to use. You simply place the mouse cursor above one of the buttons and press the left mouse button to perform the command and it will either execute immediately or open a dialog window to obtain further information first. For further information on the toolbar button commands, see Section 4.4 ― Toolbars.
3.4.3. Using Context Menu Commands
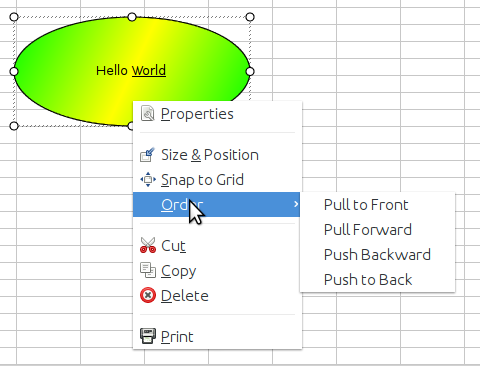
In many situations, Gnumeric provides a menu right under the mouse cursor if the right hand mouse button is clicked. This menu contains different entries depending on where the mouse cursor is when you click the right hand mouse button. For further information, see Section 4.3 ― Context Menus.
3.4.4. Using Keyboard Shortcut Commands
You can trigger certain common commands by using a combination of keys. The menu entries are often followed by a combination of keys which you can use to trigger that command. For instance, to save the file which you are currently using, you can jointly type the control key and the s key (i.e. Ctrl+S). For further information, see Appendix B ― Keybinding Reference.
3.5. Data in Gnumeric
The main purpose of spreadsheets like Gnumeric is to collect information in a coherent manner, perform calculations on the information and then be able to update those calculations easily if the original numbers change. The use of a spreadsheet therefore requires a substantial understanding of the types of information which can be entered into the spreadsheet and the methods which can be used to manipulate that information. This section explains how you can use data in Gnumeric.
3.5.1. The Types of Data in a Spreadsheet
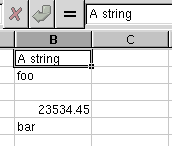
Spreadsheets like Gnumeric treat information by separating the data into separate cells and considering the data in each cell to be separate elements. Each cell in the spreadsheet has both a value, which is what Gnumeric manipulates, and a representation, which is what is actually shown. Understanding this distinction is complicated and make take some time if you are new to spreadsheets. This distinction between value and representation is one of the reasons spreadsheets are so useful.
The cells of the spreadsheet are contained in the cell grid area. The cell grid area is the area with a white background and grey grid lines. The grid lines separate this area into separate cells. Each cell has a unique reference name which is the combination of the letters of the name of the column and the number of the row. For instance, the top, leftmost cell is the cell named "A1" and the cell two over to the right and four rows down is named "C4" because it is in the column labelled "C" and in the fourth row. Each of these cells can contain only one single datum.
The datum contained in any cell will have one of five types: a text string type, a number type, a formula type, a boolean type or an error type. These five types of data values can then have various display formats so that, for instance, a number value can be displayed as a number, a monetary amount, a date or a time. Text strings are sequences of characters and punctuation marks and could, for example, contain textual information such as people's names. Number values are simply numbers but may be input and displayed in various formats including decimal numbers, dates, times, and numbers in scientific notation. Formulas are instructions to Gnumeric to calculate a result. The power of spreadsheets comes from these formulas because the results of the calculation can depend on the contents of other cells. Boolean values are either TRUE or FALSE and can be used in logical statements. Error values are usually the result of mistakes or impossible calculations.
For more advanced information on the types of data usable in Gnumeric, see Section 5.2 ― The Types of Cell Elements.
3.5.2. Putting Data into the Spreadsheet
In order to enter data into the spreadsheet, you must first select a cell in which to place the information and then actually type the information on the keyboard. Once you have entered the information, Gnumeric attempts to figure out both the appropriate data value type to assign to the cell and the appropriate data format in which to display this data value. Because this process is quite complex, you may occasionally need to actively select these parameters of the cells, which we explain in Section 3.6 ― Cell Formats below. The next two sections explain how to get data into a cell, by first moving the selection box to a desired cell and then typing the data.
- 3.5.2.1. Moving the selection box
- 3.5.2.2. Data input
- 3.5.2.3. Automatic data recognition
- 3.5.2.4. Entering text
- 3.5.2.5. Entering numbers
- 3.5.2.6. Entering a Boolean
- 3.5.2.7. Entering a formula
- 3.5.2.8. Entering an error value
3.5.2.1. Moving the selection box
In order to enter data into Gnumeric you must place the selection box over the appropriate cell. The selection box appears on the cell grid as a double lined rectangle with a small grey square in the lower right corner of the box. By default the selection box surrounds the top, leftmost cell in the cell grid area.
The simplest way to move the selection box is to use the mouse. If the mouse cursor is placed over the cell "C3" (the cursor will be represented as a thick white cross) and the left mouse button then clicked, the selection box will move to cell "C3". Note that the selection box can cover more than one cell if the mouse is dragged while being clicked. The use of these larger selections is explained below in Section 3.7 ― Complex Cell Selections.
The location of the selection box also causes the column and row headers to change slightly. The letters and numbers turn bold, and colors of the headers (the text color and the header background color) change in ways that depend on the version of Gnumeric. This helps indicate what is currently selected.
You can also move the selection box with the keyboard arrow keys. For instance, typing the right arrow twice and the down arrow once will move the selection box from the cell "C3" to the cell "E4".
The selection box can be moved in other ways and will move in response to certain actions. These movements become intuitive after using Gnumeric for a little while.
3.5.2.2. Data input
To enter data into a selected cell, you can simply start typing. The characters will then become part of the spreadsheet when you change the selection either by pressing the Enter key, which moves the selection down one cell, by pressing the Tab key, which moves the selection one cell to the right, or by selecting any other cell with the mouse. If the cursor is in the cell and not in the data entry area, pressing any of the cursor movement keys also causes Gnumeric to record the data in the cell and select another cell.
For example, you could use the mouse to select the cell four columns over (Column D) and three rows down (Row 3). Then you could type "Hello, this is a line of text." and then press the Enter key. The text would then appear in cell "D3" and, if the cells to the right are empty, would span into those cells so that the whole entry is visible. The selection box moves to cell “D4” when you press Enter, ready for the input of more data.
Note that as the data text is entered it appears in both the cell and the data entry area (the area below the toolbars and to the right of the equals (=) sign).
You can correct mistakes you make during data entry by using the Backspace key or the Delete key. Finer control can be obtained if the cursor is moved to the data entry area by clicking with the mouse in the box to the right of the equals (=) sign. Editing in the data entry area lets you use the arrow keys to move backward and forward in the text. You can also use the mouse to move the cursor.
To change the contents of a cell, select the cell again and either type the new contents or edit the existing contents of the cell in the data entry area.
If the content of the cell is too large for the size of the cell, the entry may span over the edge of the cell into the empty cells to the right. If the cell is a number, the cell grid area may display hash marks (######) to indicate the cell has content which is too large to display in the given cell width.
3.5.2.3. Automatic data recognition
As you enter data into the spreadsheet, Gnumeric interprets the information in order, first, to assign it to a data category and, second, to give it an appropriate data display format. The entry will be assigned to one of the basic data types and possibly to a sub-type. Entries which start with an apostrophe (') are considered to be text no matter what the rest of the contents. Entries which start with an equals sign (=) are automatically considered to be a formula. Entries which are single numbers or which fall into commonly used patterns for dates or times will be considered to be numbers.
Gnumeric usually figures out correctly both the type and the appropriate display format for the data being entered. Occasionally, you will have to force Gnumeric to consider the data to be a different data type than Gnumeric would guess by default. We explain the details of this process in greater detail in the extended chapter on data, Chapter 5 ― Working with Data.
3.5.2.4. Entering text
To enter text, select the appropriate cell, type the text, and then press the Enter key. If the text is too large to fit in its own cell, and the cell to its right is empty, the text will span into the cell on the right. By default, Gnumeric uses a display format for text in which the contents are shown left justified.
For more information about text elements, see Section 5.2.1 ― Text Data Elements.
3.5.2.5. Entering numbers
To enter a number, select the appropriate cell, type in the number and then press the Enter key. Gnumeric recognizes several types of information to be numbers.
The simplest kind of input which Gnumeric recognizes as numbers are standard numeric values. Technically, these are contiguous sequences of digits which may have a separator symbol between the thousands and another symbol indicating the decimal separator. These symbols follow the English convention by default (comma as thousand separator, period as decimal symbol) but will adopt the symbols appropriate for a different locality if Gnumeric is launched in a particular way (see Section 13.5 ― Languages and Locales). For instance, in a French setting the period is the thousand separator symbol and the comma the decimal separator symbol. By default, Gnumeric displays numeric values lined up against the right side of the cell.
Several other types of input are recognized as numeric values which means that calculations can be performed on the values in the cells.
- Dates in the standard format of the locale (see Section 13.5 ― Languages and Locales) are recognized as numbers. By default, 11/21/1970 will be recognized as the twenty-first of November of the year nineteen seventy. Gnumeric stores the value as the number of days since the first day of January in 1900.
- Time values, such as 10:34 or 11:23:45 PM, are recognized as number values. These values are stored in Gnumeric as fractions of the whole day.
- You can input percentage values simply by appending the percent symbol (%) to the value.
- Fractions and mixed numbers are recognized as numbers. For example, “1 1/2” is equivalent to 1.5. Note that a simple fraction, such as “3/12”, may be interpreted by Gnumeric as a date. You can prevent that by including a sign (for example, “+3/12”) or by entering the fraction as a formula (“=3/12”).
- You can also input numeric values using scientific notation. For instance, 1.003e+6 will be recognized as the value one million three thousand.
For more information on numbers, see Section 5.2.2 ― Number Data Elements.
3.5.2.6. Entering a Boolean
To enter a boolean value, select the appropriate cell, type in either "TRUE" or "FALSE" and then press the Enter key.
3.5.2.7. Entering a formula
To enter a formula, select a cell and type the equals sign (=) followed by a valid formula. If Gnumeric cannot understand the formula which is entered, it will open a dialog box which may have an explanation and gives you a chance either to re-edit the expression or to accept the entry as a text entry instead of a formula. The second choice makes it easy to re-edit the entry into a valid formula simply by fixing the formula and removing the leading apostrophe (') before the equals sign.
Formulas can be quite complex since the power of spreadsheets comes from these formulas. A simple example of the use of a formula is as follows: first, select cell B2 and input the value "3" into that cell. Second, select cell D4 and input (without the quotes) "=B2+2" and then type the Enter key. Cell D4 should display the value "5". If the value of cell B2 is changed from "3" to "100", Gnumeric will automatically update the value of cell D4 to "102".
A valid formula can be a simple arithmetic expression such as
=3+4-1
Formulas may include calls to functions. These are statements which indicate that more complex operations should be performed. For instance, a formula could be "=EXP(24)" which would give the value of e (the base of the natural logarithm) raised to the 24th power. The cell would then display "2.6489e+10".
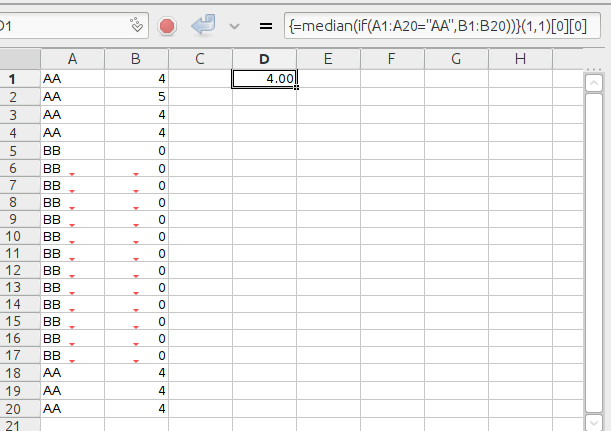
Certain functions return not just a single value but an array of values. To enter such a function, first select a range of cells to receive the result, then enter the formula to generate the array, and then press the key combination Ctrl+Shift+Enter rather than just the Enter key. For more details see Section 5.2.4.5 ― Array Formulas.
As was shown in the example above, formulas may contain references to the contents of another cell. In the example given above, the contents of the cell in the second column and the second row was used in a calculation by using the cell name "B2". These references mean that complex calculations can be automatically updated when one of the original values change.
You can make references to the cells in other worksheets and even to those in other workbooks (files). The basic format of a complete reference is made of the name of the file the reference is in, enclosed by square brackets, followed by the name of the sheet, followed by an exclamation point, followed by the letter(s) of the column name, followed by the number of the row. For example, a complete reference could be "[my_file.gnumeric]Sheet3!C3". These complete references can be shortened if the filename or sheet names are the same as that of the reference. "AE34" would refer to the cell in the current file, in the current worksheet which is in column "AE" and in row "34".
References can identify a contiguous range of cells. For instance, the reference "A1:E5" refers to all the cells from the top left corner of the current sheet to the cell five rows down and five rows over. This can be useful in a formula which uses a function such as MAX(). The formula "=MAX(A1:E5)" would display the value of the largest number value in this range of cells.
For more information on references see the complete discussion in Section 5.2.4.3 ― Cell Referencing later on in this manual.
For more on the use of formulas see Section 5.2.4 ― Formula Elements later in this manual. For a list of the functions available, see the function reference appendix, Appendix A ― Function Reference, or click on the toolbar button with the symbol "f(x)" on it for an organized list of functions.
3.6. Cell Formats
The data in Gnumeric are stored in the cells of the spreadsheet, each of which has a cell format which dictates how the data will be displayed, whether the cell will have borders and other information. Cell formatting can be quite confusing at first because it combines simple changes, such as the colour of the characters being displayed, with more complex ideas, such as how future changes to the cell will be interpreted.
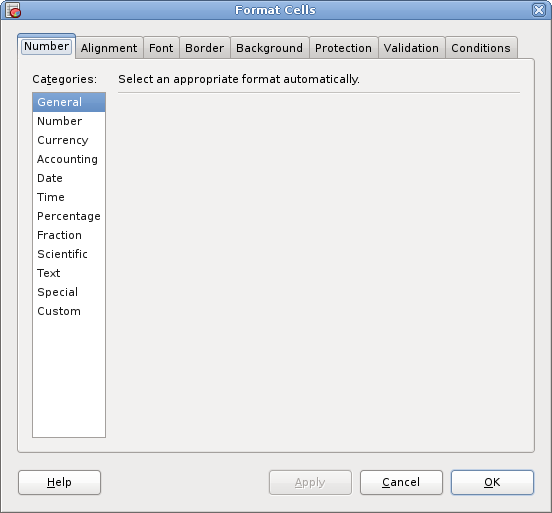
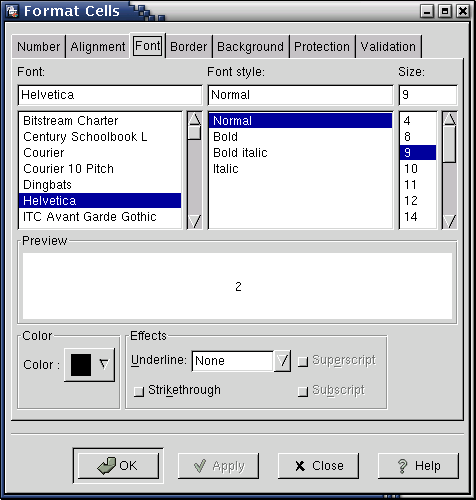
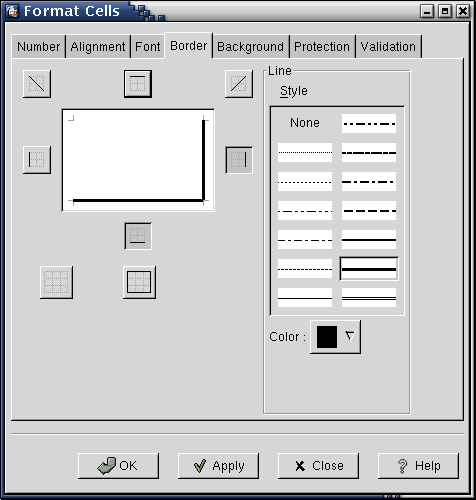
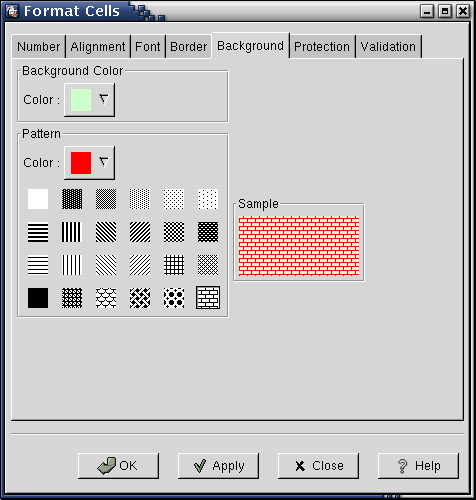
All of the cell formatting commands can be reached through a context menu by right clicking on a cell and selecting the Format Cells... menu entry. This will open a dialog window with tabs which group together similar types of formatting. Clicking on the Font tab allows you to change the font family, style, size and colour. For instance, if the cell B2 contained the text "Hello, this is my first spreadsheet" then you can make this text bigger by selecting a larger font size.
3.6.1. Simple Cell Formatting
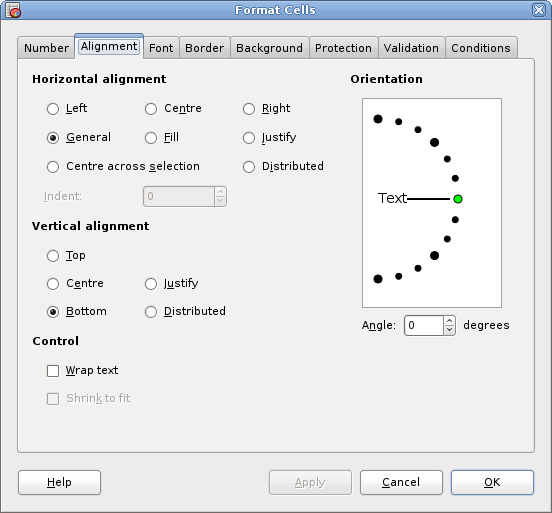
Simple changes to the format of a cell include changing the alignment of the characters, changing the font type or colour, changing the border, and changing the colour or pattern of the background.
The Alignment, Font, Border, and Background tabs are simple to understand simply by playing around with the settings and looking at the effect on a cell which contains text.
The Protection and Validation tabs are advanced functionality which you can ignore at the beginning. For explanations of these tabs, see the advanced description in Section 5.10.3.2 ― Validation Tab.
3.6.2. Formatting the Display and Entry Data Types
Cell formats are most difficult to understand when they address the type of data stored and the visual display of that data. This only arises with the options selected in the Number tab of the Format Cells dialog. While these ideas are complex, you need to understand them early on as they are fundamental to spreadsheet use.
When you enter data into Gnumeric, the spreadsheet interprets the entry based on the input format of the cell. The default format of empty cells is the General format which instructs Gnumeric to guess both the type of the data being entered and a suitable display format for that data type. However, you can change the General format to a specific format in order to alter both the way Gnumeric interprets any future data input to the cell and the way data in the cell are displayed.
Changing the format does not alter the data type of data already in a cell but does alter the display format of that data. This means that the input format will only affect future input whereas the display format will affect both the data currently in the cell and any data placed later into the cell.
For example, if you enter "12/25/2000" (without the quotes), Gnumeric guesses that this is a date and stores the value (serial number) 36885. (Usually, the value Gnumeric uses for dates is the number of days since January 1st, 1900.) 1 At the same time, Gnumeric changes the display format to display this number as a date, with a numeric month, day and year, separated by slashes.
The order in which the formatting operations occur is critical. It is not possible to alter the type of a datum currently in a cell by formatting. To alter the interpretation of the data type in a cell, formatting must occur prior to the entry of the data.
It sometimes becomes necessary to override the "General" type if Gnumeric is making an incorrect assessment of the data being entered. Postal Zip Codes in the United States, for instance, are incorrectly interpreted to be numbers. Some of these Zip Codes start with a leading zero which the "General" format type drops so the user must intervene to keep that zero displayed. In order to input these Zip Codes, the following steps must be performed. First, the cell must be selected. Next, the cell must be formatted to hold a "Text" value. This formatting changes both the interpretation of any future data entry into this cell and alters the display formatting of the cell. Finally, the Zip Code can be entered. Following these steps, the data value will be considered to be a "Text" value, any leading zeros will be retained and the data will be left justified since this is the default display format for "Text" values.
If you need to alter the data type of a whole column prior to data entry, you can do this in one formatting operation. You can click the right mouse button on the column header (the letters at the top) and select Format 1 Column from the context menu, or you can first select the whole column by clicking on the column header, then selecting the menu and the menu entry. This quick approach to pre-formatting cells can be done for any group of selected cells.
3.7. Complex Cell Selections
Selections can be more complex than a single cell at a time. Selections may describe a continuous rectangular block of cells, an arbitrary shaped group of cells or even a discontinuous group of cells.
The most common way to select a continuous rectangular block of cells uses a click and drag mouse motion. You can select the cells in this continuous block by clicking and holding the left mouse button down on one of the corner cells (for instance, the top, leftmost cell) and dragging the mouse cursor to the opposite corner (for instance, the bottom, rightmost cell) before releasing. The selection box will expand to include all of the cells in this range.
The most common way to select an arbitrary shaped or discontinuous group of cells is to hold down the Ctrl key while using the mouse to select cells. If the cell containing the mouse cursor when you click is not part of the selection, it is added, as are any other cells enclosed in the selection box when the mouse button is released. If the cell initially containing the mouse cursor is already selected, the click or click-and-drag action instead removes all the enclosed cells from the selection. As long as you hold the Ctrl key down, all of the cells included by a click or a click and drag motion will be added to or removed from the selection.
For example, to perform an operation on all the cells in a square area except those on its diagonal, begin by clicking and dragging to select the square area. Next press and hold the Ctrl key and click on each of the cells on the diagonal, removing them from the selection. You could now use to apply a format change to all but the diagonal elements of the square area.
There are several operations which cannot be performed with odd shaped or discontinuous groups of cells.
For more information and other ways to select multiple cells, see the complete discussion in Section 5.6 ― Selecting Cells and Cell Ranges.
3.8. Moving Cell Contents, Inserting New Cells or Deleting Cells
The contents of cells, both data values and formatting, can be moved from one part of a spreadsheet to another so that data do not have to be re-entered if the spreadsheet is reorganized. New cells can be added to a spreadsheet and old cells removed but these latter operations cause the layout of the spreadsheet to be altered.
- 3.8.1. Moving Cell Contents
- 3.8.2. Inserting and Deleting Cells
3.8.1. Moving Cell Contents
The simplest way to move cell contents around a spreadsheet involves selecting a block of cells containing the contents to be moved, either "cutting" or "copying" those cells, selecting the location where these contents are to be moved and then pasting the data.
Moving data can only be performed with a single selection of cells which means that only continuous rectangular blocks of cells can be moved. This does mean, however, that columns or rows can be moved as a unit. By default, Gnumeric moves the entire contents of the cells including both the data values and the formatting of the cells.
Once you have selected a group of cells, they can be "cut" or "copied" either using the menu, the toolbar buttons (a pair of scissors or two pieces of paper, respectively), the right mouse button context menu or keyboard shortcuts (Ctrl+X or Ctrl+C respectively). If cells are "cut" the contents will be removed from the current location. If cells are "copied", the contents will be duplicated in the new location. These two operations treat cell references in formulas slightly differently. If cells are "cut", any references in the cells in the new location will remain pointed at the original cells. If cells are "copied", the references in the cells in the new location will point to cells in the same relative position.
You can select the new location for the cells in two ways. The simplest is to select the top, left cell of the new location. Alternatively, you can select the whole new range of cells but the shape of this new range must match exactly the dimensions of the original range which is more difficult.
Finally you can "paste" the cell contents in the new location using either the menu menu entry, the toolbar button with a clipboard, the context menu menu entry or the Ctrl+V keyboard shortcut.
An alternative way to move cells in a current worksheet involves dragging and dropping the original selection. You select the cells to be moved as above. You then place the mouse cursor on the thick white selection border. If you click and hold the left hand button, you can drag the selected cells to a new location resulting in the same operation as a "cut" and a "paste". If you hold down the Ctrl key during the click and drag of the mouse, the result is the same as a "copy" and "paste" operation and can be repeated several times.
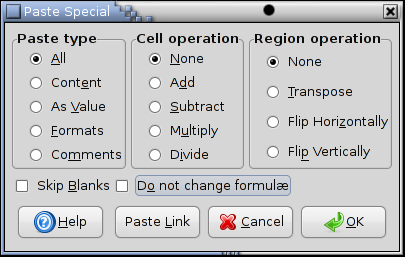
Both the menu and the context menu have an extra menu entry called which can be used during a cut and paste operation to selectively transfer some of the original cell contents or to alter the contents in specific ways. This option allows the transfer of only the cell contents, only the cell formats or only the calculated values of the cells. The transferred contents can also be mathematically combined with the current contents of cells in the new location. Alternatively, the selection can be transposed. See Section 5.7.3 ― Paste Special for more information on the command.
3.8.2. Inserting and Deleting Cells
A worksheet can also be altered by inserting or by deleting cells. These operations actually alter the locations of cells in a workbook.
Inserting and deleting columns and rows are easy to understand. If you select a group of columns or rows, selecting the or menu entries in the menu will add the same number of columns to the left of the selected columns or of rows above the selected rows. You can also use the context menu for the insert operation. The context menu can be used to delete the currently selected columns or rows.
Insert operations can result in the loss of data if the last columns or rows currently contain information.
Individual cells or contiguous rectangular blocks of cells can also be inserted and deleted. During this operation, you are asked which way to shift the current cells to allow the insertion or deletion of the selected cells. The movement can be along the rows or along the columns and will result in the relative movement of cells which were previously contiguous. This shift is the fundamental difference between insert and delete operations compared to cut or copy and paste operations.
3.9. Sheets
The worksheets in a workbook can be altered in several ways. The name of a particular worksheet can be altered. New sheets can be added. A current sheet can be duplicated or removed. The sheets can be reordered. Other sheets operations can alter the colour of the tabs or change the "protection" status of a worksheet to allow cells to be locked or hidden.
To change the name of a worksheet, right-click on its tab to access the Worksheets context menu and select . Edit the New Name field and click on OK to set the new worksheet name.
You can insert a new empty sheet after the current sheet through the menu entry in the menu or through the context menu which appears when you click the right mouse button on a tab.
Instead of an empty sheet, you can add a copy of the current worksheet to the workbook after the current sheet by selecting the menu entry from the context menu.
You can remove the current sheet using the menu entry from the context menu.
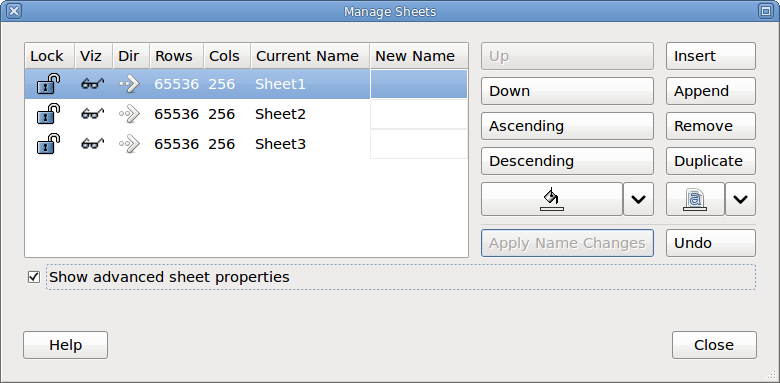
You can re-order worksheets from the Manage Sheets dialog.
Many of these operations can be performed at once from the Manage Sheets dialog which can be opened through the menu entry in either the submenu in the menu or in the sheet tab's context menu.
3.10. Graphing
A major function of moderns spreadsheets is to provide a quick and easy way to plot numerical data in graphical charts of various kinds. The use of graphs provides users a way to explore data to discover relationships and trends in the data values. Graphs also provide an effective way to present data so as to demonstrate relationships in the data and summarize large amounts of data in an effective image. In Gnumeric, both of these can be done easily and efficiently. Information on the creation of graphical displays of data is presented in greater detail in Chapter 9 ― Graphics: Images, Widgets, and Drawings.
When graphs are used to explore data, the aim is usually to produce a plot quickly with a minimum of effort. These plots are not designed to look polished but must present the required information as quickly as possible. To produce these graphs, users must learn a simple series of operations which will produce the desired plots. For speed, the most critical operation involves selecting the cells on the spreadsheet which will be used as data before starting the graphing process.
Graphs which are used to present data must be carefully crafted to communicate effectively. Clarity of communication is the critical factor and the plot may include a large amount of work to ensure that the visual result of the plot helps to communicate the desired result.
The use of a graph may not be the best way to communicate information. A verbal explanation or a simple table are often sufficient and, because they are more compact, may be more effective ways to communicate.
Graphs which use a large number of the graphical features available in Gnumeric often appear cluttered. The visual richness of such images can often obscure the message contained in the presentation of the data. Sparse, elegant and direct graphs will communicate results most effectively.
- 3.10.1. A Simple Graphing Example
3.10.1. A Simple Graphing Example
This section will introduce the process of creating a graph by presenting an example of a side-by-side column plot.
- 3.10.1.1. Data for the examples.
- 3.10.1.2. Making the Column Plot
- 3.10.1.3. Modifying the Simple Graph
3.10.1.1. Data for the examples.
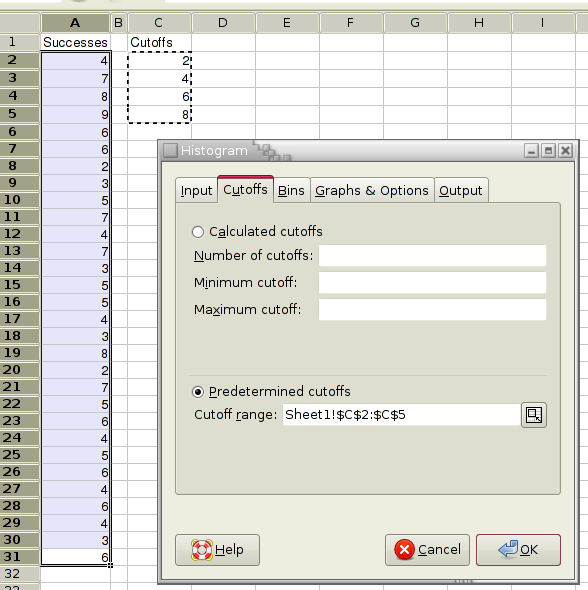
Because a graph requires data, it is first necessary to create some simple data to use in these examples. First we have to input these data into a worksheet. The data used are shown in Figure 3-3. For clarity in this discussion, the word "Interval" should be in cell A1.
3.10.1.2. Making the Column Plot
A column plot presents a series of data points as columns whose height depends on the value of each datum. This is a useful type of plot to show the number of eggs produced in each interval.
-
The quickest way to make a plot starts with the selection of the data. Using the mouse, first select the range A1:C5 which includes the data both for the number of Eggs and for the number of Females.
-
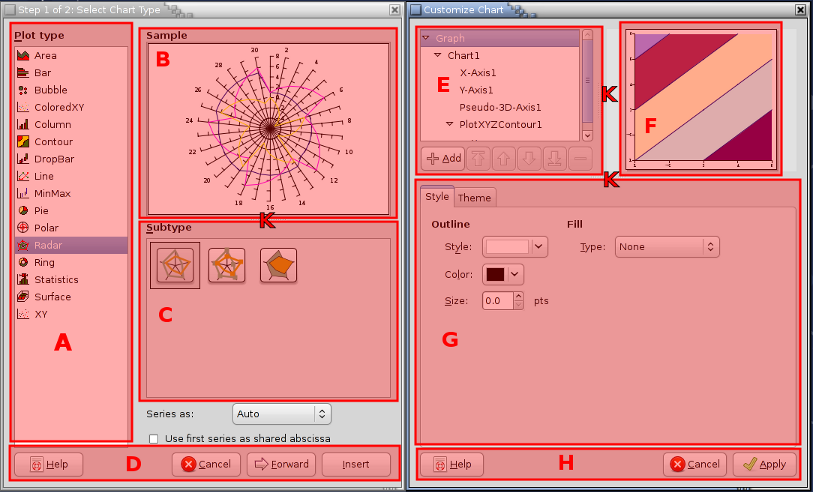
Next, click on the graphing toolbar button
 which looks like three colored pillars. This launches a
new window called the graph guru.
which looks like three colored pillars. This launches a
new window called the graph guru.
-
Next, click on the word "Column" next to the icon with vertical colored bars
 which will move the selection to that row.
which will move the selection to that row.
-
Click on the "Insert" button. This will make the druid disappear and leave the mouse cursor as a thin cross hair.
-
Finally, we will place and size the graph on a sheet. Click on the sheet and drag downward and to the right. As the mouse is dragged, a rectangle will expand. When the mouse button is released, a simple column chart should appear.
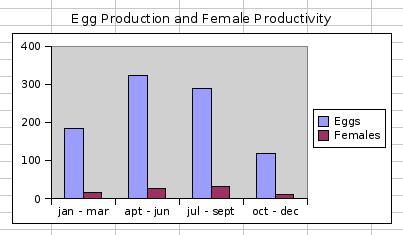
The simple graph should look like Figure 3-4.
3.10.1.3. Modifying the Simple Graph
The graph can be customized with titles, extra charts, overlaid plots, label boxes and lots of extra information. To customize the graph, right click on the plot to open the graph custom menu. The graph context menu will appear as shown in Figure 3-5.
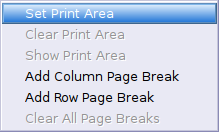
This menu provides access to several functions. Users can customize the appearance of graphs by selecting the menu item, can save the graph into PNG or SVG formats using the menu item, can reorder the various graphical elements displayed in the worksheet using the , , , and menu items or can delete graphical elements with the menu item.
If we wanted to add a title and a legend to the graph, we could use the menu item to open the graph editor and customize the graph as follows:
-
Right click on the graph to open the context menu and select the menu item. This will open the graph editor.
-
The graph editor opens with the top-level "Graph" entry selected in the element tree displayed in the top left pane of the editor. The top right pane of the editor displays a preview of the eventual graph. The bottom pane of the editor has a single or several tabs presenting the elements which can be modified for the particular item selected in the element tree. Click and hold on the button
 to open the menu of elements addable to a graph. Note that
this menu changes depending on the element selected in the
element tree when the is
clicked. Drag the mouse cursor down until the selection
highlights the "Title" entry and release the mouse
button. This will add a "Title" node in the graph element
tree and change the selection to this "Title" node. The
bottom pane of the graph editor will also change to
display the modifiable characteristics of the "Title"
element.
to open the menu of elements addable to a graph. Note that
this menu changes depending on the element selected in the
element tree when the is
clicked. Drag the mouse cursor down until the selection
highlights the "Title" entry and release the mouse
button. This will add a "Title" node in the graph element
tree and change the selection to this "Title" node. The
bottom pane of the graph editor will also change to
display the modifiable characteristics of the "Title"
element.
-
In the text field of the tab displayed in the bottom pane of the graph editor, add a title such as "Egg Production and Female Productivity" and type the Enter key. Note that the title appears at the top of the graph in the preview pane.
-
In the graph tree, select the node labelled "Chart1". Next, click and hold on the add button, drag down to the menu item and release. Note that this adds a legend on the right of the graph in the preview pane.
-
Click on the "Apply" button. The plot should now have a title and a legend. Note that Gnumeric has used the words in the column headers automatically to label the two data series in the legend.
The modified graph should look like Figure 3-6.
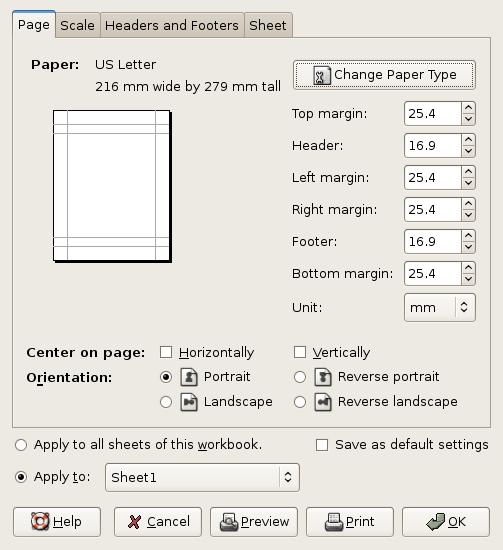
3.11. Printing
Printing in Gnumeric is quite simple and similar to other GNOME applications. Printing can be done using the toolbar buttons or can be accessed through the menu. Printing usually involves configuring the page properties (like the paper type and margins), then previewing the document to be printed and finally actually printing the document.
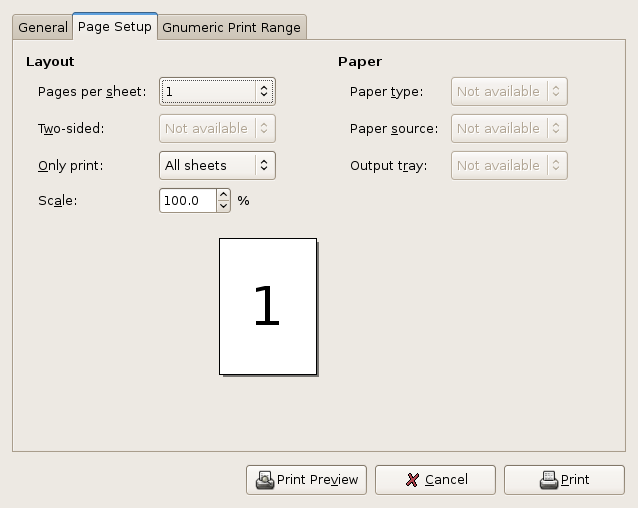
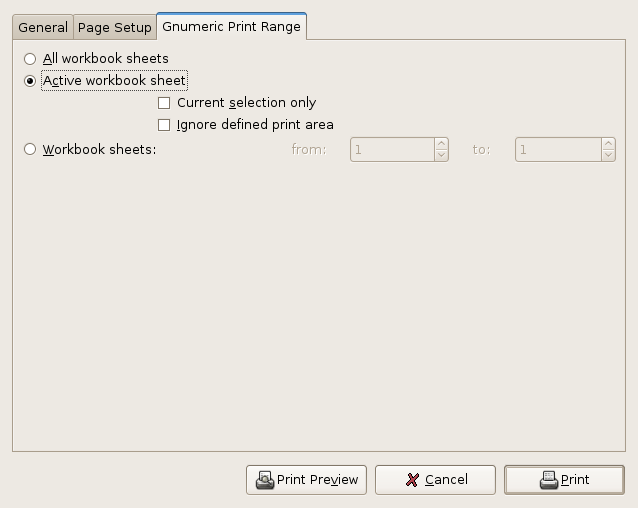
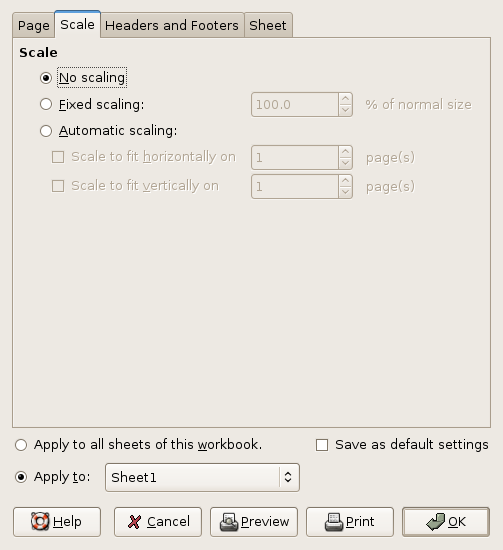
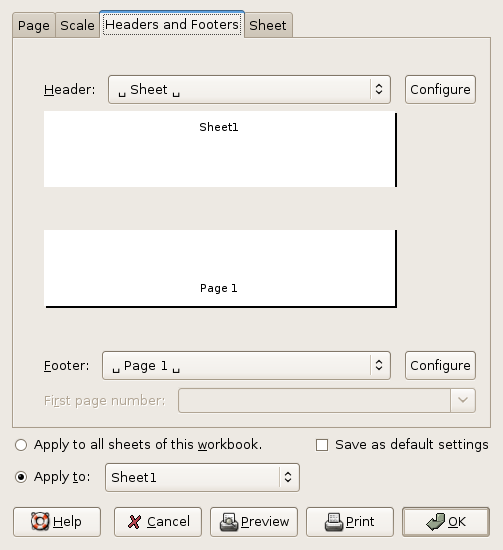
In order to configure a worksheet for printing several parameters must be set such as the correct size of the paper sheet, the layout of the spreadsheet, headers and footers and such information. These parameters can be set once for all of the worksheets in a file or separately for each worksheet. The menu entry invokes a dialog through which to alter the printing parameters.
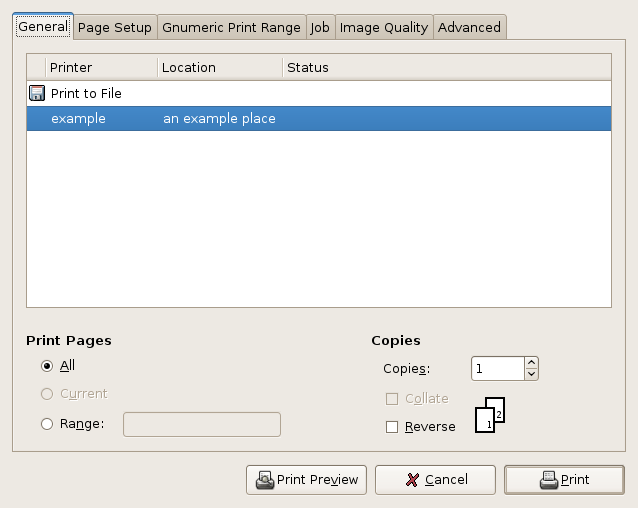
The menu item or toolbar button will open a window which shows what will be printed with the current configuration. By default, printing only applies to the current worksheet but this can be changed in the print dialog explained next.
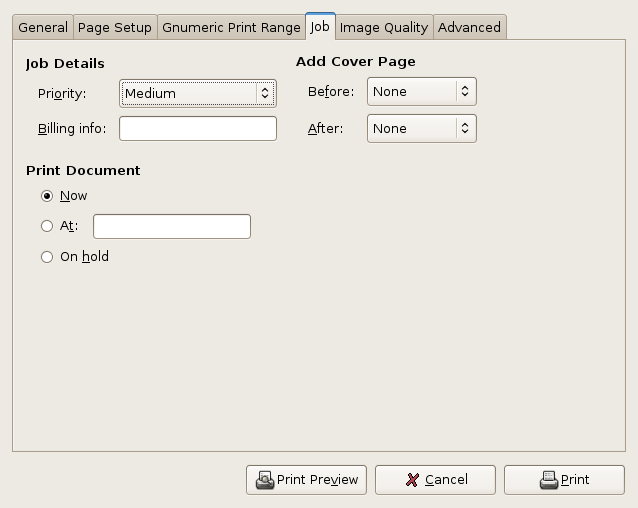
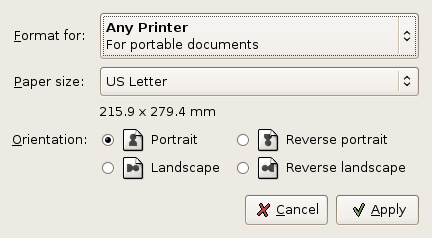
The menu item or toolbar button will open a dialog which allows the user to select whether to print to a printer or to a PostScript or PDF file. Various printers can be selected and the parameters of the job, such as whether to print all the worksheets or only the currently selected worksheet, can be altered. Clicking on the button will perform the printing task.
Printing is explained in greater detail in Chapter 15 ― Printing.
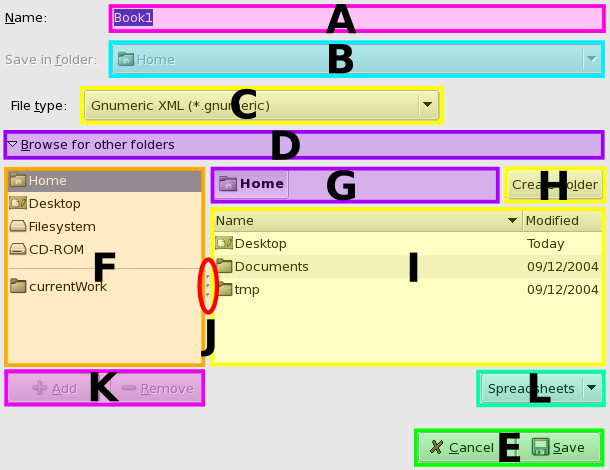
3.12. File Opening and Saving
When you first start Gnumeric a new workbook will be opened. To save this workbook into a file, click on . This brings up the file dialog where you can pick the filename and format for the book you are saving. It is best to save the book in the Gnumeric XML file format the first time. This allows you to easily edit the file without worrying about changes in the format and look of the book.
Once the file has a name and a file format, saving subsequent
changes can be done easily either through the
menu, through the toolbar or through a
keyboard shortcut. Saving with the menu requires selecting the
and then the menu item. Saving with the toolbar simply requires
clicking on
 in the tool bar. Finally saving with a keyboard shortcut simply
requires typing
Ctrl+S.
in the tool bar. Finally saving with a keyboard shortcut simply
requires typing
Ctrl+S.
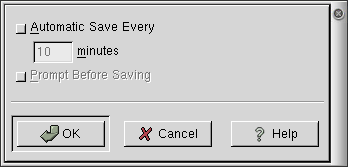
Sometimes you want your book to be saved often so you do not lose any work. To save the book at intervals click on . The Auto Save dialog appears.
Click on the button and enter the number of minutes will pass between each save. When the interval is shorter more of your work will be potentially saved, but Gnumeric might appear sluggish. If Gnumeric is sluggish increase the time between saves. The button brings up a dialog to ask if you want to save the book.Using the automatic saving feature of Gnumeric can save time but is dangerous. Gnumeric does not create a new file each time a file is saved but instead Gnumeric modifies the existing file which destroys the previous work. In certain situations, this feature can lead to the loss of possibly important work. Users are highly recommended to backup their work by copying the original file to a new name or by saving files to newly named files.
An existing spreadsheet file can be opened in several ways. If the
file has an icon on the desktop, this icon can be clicked or
double-clicked with the mouse button. Similarly, if a file
manager, such as the Nautilus file
manager, lists the file, then the file name can be clicked and
opened. If Gnumeric is already opened,
a file can be opened by clicking on the
and selecting the menu
item. Alternatively, the "Open file" button on the toolbar,
 ,
can be used or the F3 key clicked. All three of
these open the Open File dialog. You can
then select the spreadsheet file you wish to open.
Gnumeric can open many different types
of spreadsheet file formats.
,
can be used or the F3 key clicked. All three of
these open the Open File dialog. You can
then select the spreadsheet file you wish to open.
Gnumeric can open many different types
of spreadsheet file formats.
If the file has recently been opened in Gnumeric, the file name will appear in the menu and can simply be clicked to re-open the file.
3.13. Closing Gnumeric
There are several ways to close Gnumeric. The simplest is to select the menu and then the menu option at the bottom of the .
Gnumeric can also be closed through the window manager by clicking on a close box in the window frame or through a pop-up menu. The placement of the box and the invocation of the menu depend on the particular window manager and the theme being used. If the GNOME panel is running the window list applet, clicking with the right mouse button opens a context menu with a which can be used to close Gnumeric.
If any changes have been made to the workbook since the last time it was saved, a dialog will open to ask what is supposed to happen to the contents of the workbook. At this point the contents of the workbook can be saved (Save), the request to close gnumeric can be cancelled (Don't Quit) or the most recent changes can be discarded (Discard). If the user decides to save the content, a second dialog may open requesting a file name, location and type for the saved workbook.
To delete files that were created by Gnumeric any graphical file manager (such as the GNOME file manager Nautilus) or the shell command rm can be used.
4. Gnumeric Elements
This chapter describes all of the pieces of Gnumeric which a user can manipulate. The chapter provides explanations for each of the menus, menu entries, toolbar buttons and other elements of the graphical user interface.
- 4.1. Overview
- 4.2. Menus
- 4.3. Context Menus
- 4.4. Toolbars
- 4.5. Data Entry Area
- 4.6. The Cell Grid
- 4.7. The Information Area
- 4.8. The Mouse Pointers used by Gnumeric
4.1. Overview
This part of the Gnumeric manual explains the pieces of the software that users can manipulate. The menus, the toolbars and the cell grid area comprise what is called the graphical user interface of an application because it is an interface --- a way to interact with Gnumeric --- which is made of graphical elements --- pictures --- designed to be used by human users.
Gnumeric opens by default with a view of an empty workbook which is called "Book 1" and which contains three worksheets: "Sheet1", "Sheet2", and "Sheet3" as can be seen in Figure 4-1. The outermost portion of the window is not actually part of Gnumeric and may look different on different machines. Gnumeric attempts to place its name and the name of the workbook on this outer portion.
The majority of spreadsheet work is done while interacting with this view of Gnumeric. All of the functions which Gnumeric provides can be accessed quickly from here. The graphic elements of Gnumeric are made of several independent pieces. Figure 4-1 shows a newly opened, empty Gnumeric with the principle elements labelled.
The elements names are listed below along with a reference to the section that discusses that element. Those reading this document on their computers may be able to click on the references to jump to that section of the manual.
- 1 The menubar
-
The menubar provides access to the core functions of GNOME. Almost everything that can be done in Gnumeric can be done through the menus. The menus and menubar are discussed in Section 4.2 ― Menus.
- 2 The standard toolbar
-
The standard toolbar provides shortcuts for the most used items in the menus. The toolbars are discussed in Section 4.4 ― Toolbars and this toolbar in particular in Section 4.4.2 ― The Standard Toolbar.
- 3 The format toolbar
-
The format toolbar changes the display properties of data in the workbook. It is presented in Section 4.4.3 ― The Format Toolbar, part of the general discussion of toolbars of Section 4.4 ― Toolbars.
- 4 The object toolbar
-
This toolbar enables the user to draw graphic elements on the sheet, such as text labels, big red circles or thin green arrows. These can be used to bring attention to a particular part of a worksheet. The object toolbar is explained in Section 4.4.5 ― The Object Toolbar in the Section 4.4 ― Toolbars portion of the manual.
- 5 The data entry area
-
The data entry area is useful for the modification of complex formulas. It is discussed in Section 4.5 ― Data Entry Area.
- 6 The cell grid area
-
The cell area lies in the middle of all the rest. The cell area includes the row and column labels, the scrollbars and the tabs below. The use of these elements is explained in Section 4.6 ― The Cell Grid.
- 7 The information area
-
This area is used by Gnumeric to give feedback on the status of certain operations. This information is explained in Section 4.7 ― The Information Area.
The next chapters will explain each of these elements. Section 4.2 ― Menus will explain the menus, Section 4.4 ― Toolbars will explain the toolbars, Section 4.5 ― Data Entry Area will explain the data entry area, Section 4.6 ― The Cell Grid will explain the cell grid area, and Section 4.7 ― The Information Area will explain the information area.
4.2. Menus
This section of the manual describes the use of the menubar and the menus themselves. It then explains each entry in every Gnumeric menu, submenu or context menu.
- 4.2.1. Using Menus
- 4.2.2. Menubar
- 4.2.3. File Menu
- 4.2.4. Edit Menu
- 4.2.5. View Menu
- 4.2.6. Insert Menu
- 4.2.7. Format Menu
- 4.2.8. Tools Menu
- 4.2.9. Statistics Menu
- 4.2.10. Data Menu
- 4.2.11. Help Menu
4.2.1. Using Menus
A menu is a graphical element within a program which appears with a list of options. For instance, almost all applications have a menu through which the user can access the computer's filesystem to open or save their work. The main menus are on the menubar. The use of these menus is discussed in Section 4.2.2 ― Menubar.
Gnumeric also uses context menus to give users a quick way to access certain commands. The context menu will open up right under the mouse pointer when one of the secondary mouse buttons, usually the rightmost, is clicked. This menu is called a context menu because the entries in the menu are different depending on the location of the mouse pointer. The context menus are discussed in Section 4.3 ― Context Menus.
Both the main menus, on the menubar, and context menus may have submenus. A submenu is indicated by a small right-pointing arrow. To access a submenu, move the pointer down to the submenu entry. When the submenu opens, move the pointer directly across into the submenu. When there is not enough room to the right of the currently open menu, submenus may open to the left. Note that the submenu will close if the mouse pointer moves into any other menu entry.
You can also use the keyboard to navigate menus and submenus. See Section 4.2.2 ― Menubar to access the main menus using the keyboard. Once a menu is displayed, menu entries can be highlighted by pressing the down and up arrow keys. When a submenu opens, pressing the right arrow key moves the highlight to the first entry of the submenu. When a submenu entry is highlighted, pressing the left arrow key removes the highlight from the submenu. Pressing the space bar or the Enter key activates the highlighted menu entry.
Menu entries ending with an ellipsis (three dots) open a dialog window which asks for more choices.
4.2.2. Menubar
The default location of the menubar is at the top of the application window. The menus provide quick and organized access to all major commands such as opening files, saving files, printing and quitting the application.
To open a Gnumeric menu, click on the name of the menu in the menu bar. Once clicked, the menu will stay open. If the mouse pointer is moved to the name of another menu on the menubar, the first menu will close and the new menu open up. This is a useful way to look in each menu to hunt for a commands. Menus can also be opened through the keyboard. Pressing and holding the Alt key causes one of the letters in each menu name to be underlined. Press-and-hold Alt and press the underlined letter to open the associated menu. Using the keyboard for menu activation or navigation causes a letter of each menu or submenu item label to be underlined. Press that letter key to activate the menu item. Once a menu is open, the arrow keys can be used to move between menus or select an entry in a particular menu. To close an open menu, click over any other area of the application or of the desktop or press the Escape key, Esc.
Many menu entries are followed by a series of key names. These keys can be used to perform the menu action without having to open the menu. These are often combinations of keys involving the control key which is labeled as Ctrl, the shift key which is labeled Shift and the function keys which are labeled with an F and then a number. For example, to quickly cut a selection (accessible through the menu), the user can make a selection and then type the control key and the "x" key at the same time.
4.2.3. File Menu
The menu is the most important menu in Gnumeric because it gives the user the ability to interact with the computer operating system. This menu allows the user to create files containing all the work they have done. It also enables users to print the results of their work. Finally, the menu is the best way to close Gnumeric.
The menu choices are grouped into the following groups:
- 1 Workbook creation operations.
-
These menu items perform operations on files. Each item is presented below. File operations are critical and are therefore discussed in their own section latter in this manual in Chapter 14 ― Working with Files.
- — Create a new workbook. This opens a new workbook in a new window. By default the workbook will be named "Book1" or another number if there is already a worksheet with that name open. Note that the opened file has not yet been saved.
- — This menu item brings up a submenu from which a template can be selected. Rather than creating a new empty workbook, the template specifies some standard content. The new workbook is opened in a new window. The name named of the workbook is determined by the name of the template. Note that the opened file has not yet been saved.
- — The menu item opens the file chooser dialog to allow the user to pick an existing workbook for Gnumeric to open. Files in many different spreadsheet formats can be opened. To open files in a non-spreadsheet format, use the menu described in Section 4.2.10 ― Data Menu. See Section 14.2 ― File Formats for details. The menu item creates a new window containing the selected file. A more extensive discussion is presented in Section 14.3 ― Opening Files.
- 2 File creation operations.
-
- — The menu item saves the current worksheet. If the file has been named and saved before, this will silently save the file to the current filename. If it has not been saved before, this will act as if the menu item had been called and prompt the user for a filename.
- — The menu item allows users to save a file which has not yet been named to a named file. This is always used when a user saves a file which Gnumeric has named by default. This menu item can also be used to save a newly created file or to save an existing file to a new and different name. To export data from Gnumeric to a non-spreadsheet format, use the menu described in Section 4.2.10 ― Data Menu. For an explanation of the file formats which Gnumeric supports see Section 14.5 ― Saving Files.
- 3 Printing operations.
-
These menu items enable Gnumeric to print. Each item is presented below and printing issues are discussed fully in Chapter 15 ― Printing.
-
— The menu item call the Page Setup dialog. This dialog allows the user to set various printing options such as paper type, margin sizes and running header and footer formats. This dialog is explained in detail in Section 15.2 ― Page Setup..
-
— The menu item opens the submenu shown in Figure 4-4. The items in this submenu allow the print area to be set, shown or cleared; and manual page breaks to be set or cleared. The print area of a sheet is that range of the sheet that should be printed. Items outside of the print area are usually omitted when printing. When printing Gnumeric will usually choose the appropriate page breaks. Manual page breaks can be used to force Gnumeric to insert a page break prematurely.
-
— The menu item allows a user to print one or all of the worksheets in a workbook. Gnumeric can send files directly to a printer or can print to PostScript or portable document format files. The Print dialog is explained further in Section 15.1 ― Printing to a Printer or a File..
-
— The menu item calls a dialog which presents the current workbook as it would be printed with the current Page Setup settings. The dialog also permits the user to print. This dialog is explained in Section 15.3 ― Print Preview.
-
- 4 Miscellaneous Operations.
-
- — The menu item call the Send To dialog. This dialog allows the user to send a Gnumeric workbook as an attachment to an email message. This dialog is explained in detail in Section 14.7 ― Sending Files.
- — The menu item calls the Document Properties dialog, a dialog with several tabs that allow many document specific settings to be adjusted. The dialog is described in detail in Chapter 12 ― Workbook Settings.
- 5 Recently used files.
-
- The first three menu entries in this section are shortcuts to re-open recently used files. The list will change dynamically as new workbooks are opened and created. Clicking on a file name listed here is the same as using the menu entry and finding the file in the Find File dialog. Note that if the file has been moved since Gnumeric last saved it, Gnumeric will not find the file. To access any recent file not listed, one can use the menu item below.
- — The menu item opens a dialog that shows all recently used files.
- 6 The Close and Quit operations.
-
These menu items either close the current worksheet, , or close all open worksheets, . Gnumeric will prompt the user with a Save Workbook.. dialog for any workbooks that have been changed since the last time they were opened or saved.
- — The menu item allows the user to close the current workbook. If this is the only workbook which this instance of Gnumeric has open, the close operation will also quit Gnumeric. If other workbooks are open, this workbook will close without affecting the others. If the workbook has unsaved changes, Gnumeric will ask the user if he wants to save the file.
- — The menu item will close all the workbooks currently being used by Gnumeric and quit the program. Gnumeric will prompt the user asking if he wants to save any workbooks which has changes which have not been saved.
4.2.4. Edit Menu
The menu is mostly used for operations on a worksheet or between worksheets. This menu gives users powerful editing operations such as the ability to undo recent changes, the ability to cut and paste selections of cells and the ability to search for specific cell contents.
The menu choices are grouped into the following groups:
- 1 Change History.
-
These menu items allow the user to remove recent changes to a worksheet or re-introduce changes which have been undone. These options give the user control over recent edits. This functionality is often called the "change history" of an application.
The type of edit has no importance. An edit which deletes the contents of a cell is treated in the same way as an edit which adds contents to a cell. The change history is session specific. The user will not be able to undo changes through the change history if the file is saved and then re-opened. Note also that the list only covers the last few dozen operations. The number of operations which Gnumeric tracks in its history depends on the size and complexity of those operations. You can customize this number using the preference facility described in Chapter 13 ― Configuring Gnumeric. There are a few unusual operations which are not yet tracked in this way.
- — The menu item is used to remove the last few edits from a workbook. The edits must be undone in order. This menu item removes only the last edit from the workbook. The user can also access the undo list through one of the toolbar buttons and its associated menu. With this menu, the user can undo several operations at once. This is explained in section Section 4.4.2 ― The Standard Toolbar.
- — The menu item is used after an undo operation to restore the change that was undone. The menu item only restores the last undone operation. Users can also restore edit using a button on the standard toolbar and through the associated menu. The menu allows several operations to be redone at once. It is explained in Section 4.4.2 ― The Standard Toolbar.
- 2 Operations on selected areas.
-
These menu items enable selected cell contents to be moved around a spreadsheet, moved between worksheets or between workbooks. Selections are areas of the spreadsheet that have been chosen, usually with the mouse, and are usually colored pale blue. Selections are explained in greater detail in Section 5.6 ― Selecting Cells and Cell Ranges. Gnumeric currently only allows single range selections for these operations.
To use these menu items, the user must first select the range of the cut or copy area. When the user then picks these menu items, the contents of the selected areas will be entered into the Gnumeric clipboard and into the X clipboard. The contents of the Gnumeric clipboard can then be inserted into a new region of the spreadsheet, into another worksheet or into a new workbook. The X clipboard holds the space delimited results of each cell: either the text or the result of any calculation. The X clipboard can be pasted into any text area.
-
— The menu item is used to remove a selection from the selected area of a currently open workbook. When the menu item is chosen, the selected area will be outlined with a moving dotted line. This is the area which will be moved. The selection will only be removed after it is moved to the new location. Until then cut has not had an effect on the worksheet.
-
— The menu item allows a user to duplicate a selection. The original data remains where it was and the Gnumeric clipboard (and the X clipboard) has a copy which can be inserted elsewhere.
-
— The menu item is used to paste the contents of a selection which has been cut or copied. If the selection was cut, it is pasted into the new location unchanged. Cell references will not change in that they will still point to the same cells.
-
— The is used to paste a selection while altering certain characteristics. The menu item opens a dialog with three categories. The defaults make act as if it were the menu item.
The first set of choices allow the user to control the data pasted.The user can chose to limit the pasting to only the cell contents (no cell formatting is copied) or --- the opposite --- only cell formats copied (no contents). Furthermore, the user can insert the selection while transforming all the contents into values only. In this case, formulae will not be copied, only the results will be.
A second set of choices allows the user to perform simple mathematical transformations during the paste. The data in the cells being pasted into are modified by the cell contents. For instance, using the divide operation will result in each cell in the zone pasted into being divided by the equivalent cell which was copied originally.
The third set of choices allow the transposition or flip of the original selection. The transpose choice will change the selection by flipping it about the diagonal from top left to bottom right. Similarly, flip horizontally and flip vertically paste the selection accordingly.
The skip blanks check box prevents Gnumeric from taking any action for the cells in the selection that are blank. Normally Gnumeric will modify formulae that use relative addressing to cells outside the selection. The do not change formulae checkbox suppresses this change. (Note that references to cells within the selection are always preserved.)
-
- 3 Data entry and removal operations.
-
These operations add or remove data from the worksheet. They differ in the type of data modified or removed and the possible re-arrangement of remaining data, as explained below. With one exception noted below, these operations are like the previous group in acting based on the selected cells.
-
opens a submenu with eight choices, organized into two sets of four. The first group affects all cells in the selection. The second group applies the same actions to just the selected cells that are in rows selected by the filter. See Section 5.12 ― Filtering Data for details of setting up a filter.
Choose to clear all the elements of the cells in the selection: the formats and hyperlinks, the comments, and the contents. Choose to clear the formats and hyperlinks while leaving the data or formula in the cell intact. This removes any borders, re-sets the cell alignments, changes the background colour to white and the text colour to black, resets the number format to General, and removes the hyperlink associated with each cell, if any. Choose to delete the comments for the cells in the selection. Choose to leave the cell's formatting in place but remove the formula or data contents of the cell.
-
opens a submenu with five choices. They permit deleting a range of rows or columns, deleting just the selected cells, or deleting just the comments or hyperlinks associated with the selected cells.
Choose or to delete the columns or rows, respectively, that cover the cells in the selection. Selecting when the selection is one or more columns or when the selection is one or more rows deletes all cells in the worksheet. The space left by deleted rows is filled by moving lower rows up. The space left by deleted columns is filled by moving to the left columns which were right of the selection. For example, if columns D and E are deleted, Gnumeric will move the contents of all columns from F onwards two columns to the left.
: If the selection is one or more columns or one or more rows, deletes the selected columns or rows as described above. If the selection is a block of cells, opens a dialog asking how to fill in the deleted cells. Blocks of cells can be filled in by the columns of cells below the block selection or by the rows on the right of the block.
For example, if the block of cells from E6:G8 is deleted, those cells would be filled in by the cells below E8, F8 and G8 if the Shift cells up option were chosen. The cells to the right of G6, G7 and G8 would fill in the space from the right if the Shift cells left option were chosen. The two Delete choices are the same as and .
: This is the same as , described above.
: This is similar to , as described above, except that existing cell formats are not disturbed.
-
opens a submenu with three choices:
- opens the dialog. This is the same as the dialog for on the Section 4.2.6 ― Insert Menu. See Section 5.15 ― Comments in Cells for more information.
- opens the dialog. This is the same as the dialog for on the Section 4.2.6 ― Insert Menu. See Section 5.16 ― Hyperlinks for more information.
- opens the dialog. Section 5.17 ― Defining Names explains names and describes the dialog.
-
- 4 Search and replace operations.
-
- — The menu item opens a dialog to search for cells with particular content. The dialog has three tabs. In the first the user can enter the information the user wants to find and some constraints on the search. The second tab gives some extra choices for the search. When the user has picked the options they prefer, pushing the search button on the first tab will run the search. The third tab will show which cells match the search.
- — The menu item will launch a dialog to find cells with particular characteristics and replace them all with a common content. This dialog is similar to the Search dialog.
- 5 Other operations on worksheets.
-
-
— From the submenu you can perform operations on the worksheet as a whole. These functions are also available from the worksheet tab context menu. You can create, duplicate, rename, re-order, or delete worksheets. These functions are described in detail in Section 11.6.2 ― Worksheet Tab Context Menu.
-
— The menu item allows the user to select various portions of the worksheet. When selected it opens a submenu.
- The item provides a quick way to select the entire worksheet.
- The and items allow the user to select all the rows or columns spanned by the current selection.
- The menu item allows a user to select all the cells which are part of the same array as the current cell.
- The menu item selects all the cells which contain formula that reference data in the current cell.
- Similarly, the menu item selects all the cells whose data is referenced by the formula in the current cell.
- The menu item selects the next sheet object on the current sheet. If no object is selected it will select the object locate at the front.
- The , , , , menu items move the selection within a rectangular block of data cells. the front.
- — The menu item opens up a dialog which allows the user to type the name or address of a cell in the worksheet. The current view will then change to ensure that the selected cell is in the current view and the selection will cover that cell.
-
— The menu item forces the workbook to recalculate its results. This is useful if a formula in the current worksheet depends on a cell in a different workbook. Gnumeric will not necessarily know when that data has been updated so a user can force Gnumeric to recalculate all the cells in the current workbook.
-
- 6 General Configuration of Gnumeric.
-
— The menu item calls the Gnumeric Preferences dialog explained in detail in Chapter 13 ― Configuring Gnumeric
4.2.5. View Menu
The menu is
The menu choices are grouped into the following groups:
- 1 Alternative views of the current document.
-
These menu items allow the user to open multiple views of the same document.
-
— The menu item opens up a new window with the current workbook visible. and where both windows are open to the same section of the workbook. If the user starts editing a different part of the sheet in one view, the other view moves automatically to that portion of the worksheet. Similarly, if the user changes to a different worksheet in one view, the other view changes also.
-
— The menu item is used to freeze the top-most and leftmost visible portion of the worksheet. This is useful to be able to line up portions of the worksheet which are not usually together. For instance, if a user had a very large table with the titles of each column of data on row 12, the user could select row 13 and select this menu item. If the user scrolled through each data row, the data would line up underneath each header.
There are 3 ways to determine which rows and/or columns should be frozen.
- If the selection is at least partially visible and does not include the cell A1, Gnumeric freezes the portion of the worksheet above or to the left of the current selection.
- If the selection is at least partially visible, includes cell A1, and does not consist of whole rows or columns, Gnumeric freezes all rows or columns intersecting the selection.
- If the selection is at least partially visible, includes cell A1, and consists of whole rows or columns, Gnumeric freezes those rows or columns.
- If the selection is not visible at all, then Gnumeric freezes those rows and columns to the left or above the sixth visible column and tenth visible row.
In all cases, the region of the worksheet above or to the left of the currently visible region will become inaccessible until the view is unfrozen.
-
— The menu item provides access to a submenu which lists all of the windows which are currently open. This provides an easy way to jump between all the different instances and views of Gnumeric documents.
-
- 2 Changes to the current view.
-
These menu items alter the display of the current view.
-
— The menu item provides a submenu which lists each Gnumeric toolbar. The toolbars in this submenu which have a check mark in front of their name will be shown. The display status of each toolbar can be changed by selecting the menu item with that toolbar's name.
-
— The menu item determines whether to display the status bar and information area at the bottom of each worksheets. Selecting the menu item toggles the check mark in front. When this menu item has the checkmark, Gnumeric will display the statusbar.
-
— The menu item changes the display of Gnumeric from a window based display to a display which occupies the whole screen. In full screen mode, the window borders will not be displayed nor will the toolbars. The key F11 toggles between full screen and regular display mode. When this menu item has the checkmark, Gnumeric is in mode.
-
— The menu item opens the dialog.
The dialog has four tabs. is described in Section 11.4 ― General Settings, in Section 11.4.1 ― Content Protection.
The check boxes on the tab shown in Figure 4-11 determine whether cells are shown with indicators that they contain formulae and/or that they have clipped content.
The check boxes on the tab shown in Figure 4-10 determine whether the notebook tabs, the horizontal scrollbar and/or the vertical scrollbars are shown in this view.
-
- 3
-
opens a dialog where you can set the magnification of one or more worksheets in the current workbook.
4.2.6. Insert Menu
The menu is
The menu choices are grouped into the following groups:
- 1 Insert into workbook.
-
These menu items alter the cells available in a workbook.
-
— The menu item opens a dialog asking the user how the sheet should be altered when new cells are inserted. The dialog lists four choices. The user can choose one of these by clicking the mouse pointer on one of the four dots. Only one choice is possible and the currently selected choice has a black dot in front.
The Shift cells right will insert a region of new cells of the size of the current selection. Cells which are on the same row as the selection and within or to the right of the selection will shift over to the right to accommodate the new cells. The Shift cells down choice will also insert a region of new cells the same size as the current selection. With this choice, cells which are in the selection or below the selection will move down to accommodate the new cells. The two other choices will act as if the user had chosen to insert rows or columns. These actions are explained above.
-
— The menu item will insert columns to the left of the current selection. The number of columns inserted will equal the number of columns spanned by the current selection.
-
— The menu item will insert rows above the current selection. The number of rows inserted will be equal to the number of rows spanned by the current selection.
-
— The menu item allows the user to insert a worksheet immediately following the current sheet.
-
- 2 Insert an object into the worksheet or content into the current cell.
-
The menu items insert sheet objects into the worksheet or insert content into the current cell.
-
— The menu item will allow a user to insert a graphic plot of data. This menu item will launch the graph druid. Graphing in Gnumeric is explained in Chapter 10 ― Graphs.
-
— The menu item will allow a user to insert a graphic object containing the image from an external file. The use of images in Gnumeric is explained in Section 9.2 ― Images.
-
— This menu item opens a dialog to allow the user to enter a mathematical formula into the cell. The function dialog includes the names and a brief explanation of all the available functions.
-
— Selecting an item from the submenu shown in Figure 4-13 replaces every rectangular region in the current selection with an array function in which the appropriate function is wrapped around an array version of the current content. This can be used to create a self-sorting data region.
-
opens a dialog with a list of all defined names that can be pasted into the current cell. The dialog is similar to the dialog opened by choosing from the Section 4.2.4 ― Edit Menu. See Section 5.2.4.4 ― Names for details.
-
opens a dialog where you can enter or edit a comment for the active cell. The dialog is described in Section 5.15 ― Comments in Cells.
-
opens a dialog for entering the location of a link. The dialog is described in Section 5.16 ― Hyperlinks.
-
opens a submenu from which you can insert predefined content into a cell. You can insert the current date, the current time, or both.
-
4.2.7. Format Menu
The menu allows users to control the formats of cells, columns, rows, worksheets and the workbook. This menu also gives users access to templates of standard formats.
- offers these menuitems:
-
-
— The menu item opens a submenu with choices to allows the user to modify the formatting of the selected cells.
- — The menu item opens the cell format dialog. This dialog is used to set cell data types and formats. It is explained in Section 5.10 ― Formatting Cells.
- — The menu item opens the conditional format dialog. This dialog is used to set cell data types and formats that depend on values in the workbook. It is explained in Section 5.11 ― Conditional Formatting of Cells.
- — This menu item combines the current selection into a single large cell.
- — This menu item divides a merged selection into the original cells.
- — This menu item makes Gnumeric automatically choose the optimal row heights to display all of the text in the current selection.
- — This menu item makes Gnumeric automatically choose the optimal column widths to display all of the text in the current selection.
-
— The menu item opens a submenu with choices to allows the user to modify the view of the selected columns.
- — The menu item opens a dialog to enable the user to adjust the size of the columns which hold the current selection. The dialog has a single entry box in which the user can change the current size of the column in points.
- — This menu item makes Gnumeric automatically choose the optimal column size to display all of the text in the current selection.
- — The menu item will hide the columns containing the current selection. Gnumeric still holds these columns in memory and will save them to a file but will not display those columns. The only indication that a user has that columns have been hidden is that the column header names are not sequential.
- — This menu item will show columns which are hidden if the selection spans the two columns on either side of the selection. If columns D, E, and F have been hidden, the selection must span at least across columns C and G for this menu item to unhide columns D, E, and F.
- — This menu item allows the user to resize the columns which hold the selection to the standard size. At 100 percent zoom this is 48 points or 64 pixels.
-
— The menu item provides the same functions as the menu item but operates on rows.
- — This menu item opens a dialog which allows the user to type in a row height in pixels.
- — This menu item changes the rows which hold the selection to the optimal height to hold the text in the selection.
- — The menu item will hide the rows in the selection. The workbook still contains the data in the hidden rows but those rows are not shown.
- — This menu item will make hidden rows visible. The selection must span the rows which are hidden for this menu item to unhide the hidden rows.
- — This menu item resizes the rows back to the default height of 12.75 points or 17 pixels (at 100 percent zoom).
-
opens a submenu where you can change properties of the current worksheet. With the exception of and , all operations on this submenu apply to just the current worksheet.
- 1 Sheet Management
-
These items are also on the worksheet tab context menu, accessed by clicking (usually with the right mouse button) on one of the worksheet tabs.
opens a dialog from which the names and many properties of all the sheets can be managed. Properties that can be managed from this dialog include locking, worksheet visibility, column display order (left to right or right to left), sheet name, sheet order, and sheet tab appearance. From this dialog you can also add new worksheets and duplicate or remove existing worksheets. For more information, see Section 11.6.3 ― Manage Sheets dialog.
opens the Rename Sheet dialog. Edit the sheet name in the New Name: field and press Enter or click to change the worksheet name.
- 2 Sheet Display Toggles
-
The second section contains various toggles that control how a worksheet is displayed. If a toggle is enabled, a small check mark is displayed to the left of the menu item.
- — When this property is enabled, the worksheet will show the actual formulae for all cells with formulae, instead of showing the calculated result. You can use this property to quickly determine which cells contain data and which contain formulae.
- — When this property is enabled, Gnumeric uses R1C1-style notation to address cells, rather than A1 notation.
- — When this property is enabled, Gnumeric displays all cells which would display a zero value as empty cells. This can be used to more easily find cells with non-zero data in sheets with many zero results.
- — When this property is enabled, Gnumeric does not draw the grid lines that ordinarily separate cells.
- — When this property is enabled, Gnumeric does not display the column headers, which leaves room in the cell grid for roughly one more row of cells of default height.
- — When this property is enabled, Gnumeric does not display the row headers, which leaves slightly more room to display the contents of cells.
- — When this menu item is selected, Gnumeric switches between left-to-right sheets and right-to-left sheets. If row headers are displayed, they are moved to the right-hand side of the cell grid when the worksheet is displayed right to left.
- 3 Zoom...
-
opens a dialog where you can set the magnification of one or more worksheets in the current workbook.
-
— This menu item opens the autoformat dialog to give user access to a list of format templates. Format templates are useful for users who are often filling out tables in a particular format. The user picks an area of the worksheet into which they want to apply the template. Most templates define headers and footers so the selection area must be big enough to fit those template elements and the user's data. The template will not affect data which has already been input into a worksheet.
The dialog has two tabs: Preview and Template Details. The details are simply information about the template. The Preview tab has three main options: a Settings menu, an Edit menu and a category chooser. The settings menu allows a user to pick what parts of the template they want to copy into the worksheet. The edit menu will be used to create new templates. Currently templates are written as text into an extensible markup language (XML) format. The category chooser gives the user access to different groups of templates. Templates in each category are displayed in the middle area of the dialog. Users select the template they want to use by clicking on it. The currently selected template is highlighted with a red boundary which may be hard to see.
-
4.2.8. Tools Menu
The menu is
The menu choices are grouped into the following groups:
- 1 Automatic tools
-
These two tools allow the user to make Gnumeric automatically correct typing or automatically save workbooks at periodic intervals.
- — The menu item opens a dialog which allows the user to configure the way in which Gnumeric automatically corrects text which is being entered. The dialog presents the user with three tabs. Each of these tabs allows the user to correct one type of common spelling mistake, while allowing the user to add exceptions to the rules. Gnumeric can automatically capitalize the names of week days. Gnumeric can automatically change an entry which starts with two capital letters to only start with one and Gnumeric can change a sentence entry to start with a capital letter.
- — The menu item opens a dialog which allows the user to have Gnumeric automatically save the current workbook after a fixed interval of time. The user can also have Gnumeric ask for confirmation before saving so that the user always remains aware of the state the workbook was in when it was saved.
- 2 Linear programming, scenario generation, simulation and statistical analysis tools
-
Gnumeric can be used to solve systems of linear equations and other mathematical problems. These two dialogs enable access to these tools. A full discussion of these tools is presented in Section 7.1 ― Solver.
- — The menu item opens a dialog through which the user can configure Gnumeric to iteratively search for a numeric value which solves a formula. This dialog is explained in Section 6.3 ― Goal Seek Tool.
- — The menu item opens a dialog through which the user can configure Gnumeric to solve linear systems of equations. This is explained in Section 7.1 ― Solver.
- — The menu item displays a submenu with two entries. The menu item opens a dialog in which the user can select previously defined scenarios. The menu item opens a dialog in which the user can define the contents of a new scenario.
- — The menu item opens a multipaned dialog allowing the user to configure the parameters for a simulation using linear modeling constraints.
- 3 The Plug-ins dialog.
-
This entry launches the plug-in management dialog. Plug-ins are programs which are separate from Gnumeric but provide useful functionality. Some of the core parts of Gnumeric, such as Excel file format support, are actually plugins. This means that a user who never uses Excel files can remove this module from Gnumeric and make Gnumeric use less memory.
4.2.9. Statistics Menu
The menu is
The menu and its submenus contain all available statistical analysis tools. These tools are explained in Chapter 8 ― Statistical Analysis.
4.2.10. Data Menu
The menu is
The menu choices are grouped into the following groups:
- 1 Data Field tools.
-
These menu items allow the user to re-organize data.
-
— The menu item opens a dialog which allows users to sort a selection according to defined criteria. By default Gnumeric sorts the rows in a selected area depending on the contents of the cells in a particular column of each row. The sort criteria can be extended to calculate on the basis of the cells in several columns. Gnumeric can sort a selection using any number of rules. Rules can be added using the button. Rules with no column entered will be ignored or the user can remove these rules with the button.
For each rule, the dialog has an entry box in which the column to be sorted must be entered. The dropdown box (the little down pointing arrow) will show a list of appropriate columns. The user can determine a sort order for the selection. The button allows the user to further characterize the sort criteria..
If the first row of the selection is a header, Gnumeric can be told not to shuffle this row during the sort. Gnumeric can also sort columns based on the contents of cells in specified rows, instead of shuffling rows on the basis of columns, if the user toggles the Sort to act right-left instead of top-down.
-
— The menu item opens a dialog that allows users to shuffle a selection. Shuffling means to rearrange the cells in the selection into a random order. The dialog allows users to shuffle the data within a column, within a row, or within an area.
-
— The menu item opens a submenu that allows various forms of data to be created.
-
— The menu item opens a submenu with three entries: , , and entry. Filters are explained in Section 5.12 ― Filtering Data.
-
— The menu item opens the cell format dialog to the validation tab. Validation is a means of constraining the contents of a cell either to have a certain value or to fall within a certain range.
-
— The menu item opens a dialog box through which a user can create derived information based on data in other worksheets.
-
—
-
— The menu item provides a submenu through which users can group rows or columns into units which can be collapsed to be hidden from view. These entries also allow users to alter the display of the grouping handles on the borders of the worksheet.
-
- 2 Data Modifications or Import.
-
These entries allow user to convert data already in a worksheet or to import external data directly into a worksheet.
-
— The menu item opens a dialog box through which a user can create derived information based on data in other worksheets.
-
— The menu item provides the following submenu:
The items in this submenu allow the user to import data from various non-spreadsheet formats. To open files in a spreadsheet format, use the menu described in Section 4.2.3 ― File Menu. See Section 14.2 ― File Formats for details. These submenu items create a new window containing the selected file. A more extensive discussion is presented in Section 14.3 ― Opening Files.
-
— The menu item provides the following submenu:
The items in this submenu allows users to export the current file or sheet to a non-spreadsheet format. The menu item repeats the last export in the current session or, if the file was recently imported, exports the file to the original source. To save data from Gnumeric in a spreadsheet format, use the menu described in Section 4.2.3 ― File Menu. For an explanation of the file formats which Gnumeric supports see Section 14.5 ― Saving Files.
-
4.2.11. Help Menu
The menu is quite simple.
The menu connects users to this manual, to the list of functions available for use in Gnumeric and to the list of people who created this wonderful application.
- 1 Entries to find help and report a problem with Gnumeric
-
These menu items allow the user to obtain help from several sources or to report a problem with the program.
-
— This menu entry allows the user to launch the local help system and display this manual.
-
— This menu entry allows the user to launch a web browser and explore the web site dedicated to Gnumeric on the server used by the GNOME project.
-
— This menu entry allows the user to launch an Internet Relay Chat (IRC) client to join the GIMPnet network and the #Gnumeric channel. This channel is used by the Gnumeric developers. There is generally someone around who will, after a few minutes, notice a nice question and attempt to answer it.
Live assistance is provided on a purely voluntary basis. There are no guarantees that your question will be answered or that the answer will be correct. We generally try our best to answer questions when they are asked politely and when the user shows that they have at least looked in the User Manual for an answer.
-
— This menu entry allows the user to launch a web browser and open the page on GNOME's GitLab issue/ bug entry system for the Gnumeric program. This page includes instructions on submitting reports of problems. The first time a user reports a problem, they will be asked to login to the system.
-
- 2 The About Gnumeric dialog.
-
—Shows basic information about Gnumeric, such as the authors' names and the application version number.
4.3. Context Menus
Context menus are menus which open up under the mouse pointer and are therefore detached from the format graphical structure of the application. These menus provide an extra and convenient way to access Gnumeric commands. All of the commands in context menus are available through the regular menu system. Context menus provide different commands depending on the position of the pointer.
To activate a context menu, a user simply positions the pointer over the appropriate area and clicks one of the buttons on their mouse. Since this button is configurable and users have mice with different buttons, it may be a different button on any given machine or may even require the combination of a keyboard key and a mouse buttons. The user will have to find how to do this themselves.
Currently Gnumeric provides five different context menus. The context menu that is called in the central grid area is discussed next in Section 4.3.1 ― The Context Menu for the Cell Grid Area. The Context menu that appears when the pointer is over the row headers or column headers is presented in Section 4.3.2 ― The Context Menu for Column and Row Headers. Another context menu relates to the worksheet tabs and is explained in Section 4.3.3 ― Context Menu for Worksheet Tabs. Yet another context menu applies to embedded objects or shaped components such as a plot. These are shown in Section 4.3.4 ― The Context Menu for Embedded Objects and Components.
4.3.1. The Context Menu for the Cell Grid Area
The context menu in the cell grid area appears when the pointer is over the cell grid area. This menu applies to the cells that have been selected, not necessarily the cell underneath the mouse pointer.
The grid context menu merely provides an extra way to access Gnumeric commands. The , , , , , , , , and commands are taken from the menu and its submenus and are explained in Section 4.2.4 ― Edit Menu. The and menu items are explained in the section on the menu in Section 4.2.6 ― Insert Menu. The , items as well as the items on the , , and submenus are explained in the manual section on the menu in Section 4.2.7 ― Format Menu.
4.3.2. The Context Menu for Column and Row Headers
The Context Menu for Column and Row Headers
The context menu which relates to column or row headers is similar to the context menu for the grid area. Both insert and delete operations are modified to operate explicitly on rows or on columns.
4.3.3. Context Menu for Worksheet Tabs
The context menu for worksheet tabs provides access to functions that manipulate worksheets as a whole, rather than their contents.
The context menu for the worksheet tabs provides the same functions as the submenu of the menu. These functions are explained in Section 11.6.2 ― Worksheet Tab Context Menu. There are also two submenus where you can select one of the existing sheets, whether its tab is currently visible or not. The first submenu lists the sheets in their current order, the second submenu lists them alphabetically.
4.3.4. The Context Menu for Embedded Objects and Components
The Context Menu for Embedded Objects and Components.
All embedded objects, such as drawing elements, graphs and images, have a context menu which can be invoked by placing the mouse pointer over the element and clicking with one of the secondary mouse buttons.
The first menu entry, labeled , will open a dialog specific to the type of element selected in which the user can configure the properties of the element.
The menu entry labeled , will open a dialog that permits the user to adjust the size and position of the embedded object.
The menu entry labeled , enlarges the object such that all of its corners are located at cell corners.
The menu entry labeled , opens a submenu which allows the user to change the visual order in which the graphical elements are placed. This order will affect the way in which the graphical elements obscure each other.
The menu entries labeled , , and , allow the user to operate on the whole object at once. The menu item allows the user to remove the element from its current position and then paste the object in a different location on the same sheet, in a different worksheet, in a different Gnumeric file, or in a file from a different program entirely. The menu item provides the same functionality while leaving the original item in place. The allows the user to remove the graphical element entirely.
The remaining menu item, , allows just the selected object to be printed.
For certain types of objects, a menu entry labeled allows the object to be saved as an image file. This menu item is not present in Figure 4-26 but is shown in Figure 4-28 .
Graphs have a context menu that also contains menu entries labeled and . The menu item shows the graph by itself in a window. The copies the graph to a special sheet in the current workbook that contains only a single graph.
4.3.5. The Context Menu for Toolbars
The Context Menu for Toolbars
The context menu for toolbars allows the user to configure toolbars. Each toolbar can be displayed above the sheets, to the left of the sheets, or to the right of the sheets. The context menu can also be used to hide a toolbar. The toolbar can be made visible again via the submenu of the menu. See Section 4.2.5 ― View Menu.
4.4. Toolbars
The toolbars contain buttons and other elements which can be used to perform quickly some the more common operations. Each button has an icon intended to provide a mnemonic reminder of the operation performed by the button. The toolbar elements are intended to provide fast access to the commonly used tools. Almost all of these functions are also available through the menu system. The specific actions required to use each button vary.
Gnumeric has four toolbars, the standard toolbar, the format toolbar, the long format toolbar, and the object toolbar. The three toolbars are shown in Figure 4-30.
These toolbars will be discussed separately in the subsequent sections of this manual. User interaction with each toolbar happens in essentially the same way. Similarly, the toolbars can be configured in the same way. The next section explains the standard behavior of Gnumeric toolbars.
The long format toolbar contains all of the buttons of the format toolbar plus a few extra buttons, but in a different order. Users will usually choose only one of these toolbars to be displayed.
- 4.4.1. General Toolbar Behavior
- 4.4.2. The Standard Toolbar
- 4.4.3. The Format Toolbar
- 4.4.4. The Long Format Toolbar
- 4.4.5. The Object Toolbar
4.4.1. General Toolbar Behavior
The toolbar context menu described in Section 4.3.5 ― The Context Menu for Toolbars can be used to determine where each toolbar (above the sheets, to the left of the sheets, or to the right of the sheets) is displayed. The submenu of the menu (see Section 4.2.5 ― View Menu) can be used to determine which toolbars are visible.
If the Gnumeric window is too small to fit all of the toolbar buttons, Gnumeric displays an arrow to indicate that there are more options. If the user clicks on this arrow, a window will open with the remaining buttons as shown in Figure 4-31.
Certain toolbar options, such as the zoom box, are combinations of a button or text entry area and a downward pointing arrow. If the user clicks on the arrow, a list of available options appears.
4.4.2. The Standard Toolbar
The standard toolbar is shown in Figure 4-32.
The Standard Toolbar gives the user access to file operations, printing, movement of data blocks, the undo system, and to some of the powerful tools like the function creator and the graphing system.
-
 New File.
New File.
-
Create a new file.
-
 Open
Open
-
Open an existing file.
-
 Save
Save
-
Save the current worksheet to disk.
-
 Print
Print
-
Print the current worksheet or workbook to a file or a printer.
-
 Print Preview
Print Preview
-
Display a print preview of the current worksheet.
-
 Cut
Cut
-
Copy the cells in the current selection to the clipboard buffer and mark them to be deleted from the current position. The cells will only be removed if they are pasted into a new position.
-
 Copy
Copy
-
Copy the cells in the current selection to the clipboard buffer.
-
 Paste
Paste
-
Paste the contents of the clipboard buffer into the active cell.
-
 Undo
Undo
-
Undoes the last operation undertaken.
-
 Redo
Redo
-
This is the reverse of the undo operation, restoring its original state.
-
 Insert a hyperlink
Insert a hyperlink
-
This button opens a dialog to allow the user to define a hyperlink either internally within the spreadsheet or to an external resource such as a web page.
-
 Sum into the current cell
Sum into the current cell
-
Starts a simple sum formula in the selected cell with Gnumeric simply waiting for a selection to be made to complete the sum. The user selects the destination cell, pushes this button, enters the range to be summed and pushes the confirm button (green arrow) in the data entry area or types the Return key.
-
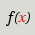 The function druid
The function druid
-
This button will start a formula in the current cell using the function druid.
-
 Sort Ascending
Sort Ascending
-
Sorts the selected region in ascending order based on the first column selected.
-
 Sort Descending
Sort Descending
-
Sorts the selected region in descending order based on the first column selected.
-
 Graph
Graph
-
This button calls the graph druid to create a graph.
-
 Zoom
Zoom
-
The zoom button allows the users to trade-off the extent of the worksheet which is visible against the size of the visible text and cells.
4.4.3. The Format Toolbar
The Format Toolbar
-
 Font Chooser.
Font Chooser.
-
The user can change the font of a selection either by typing the name of a new font in the text area of this box or by clicking on the little arrow to the right of the text area. This will cause a menu to appear from which a font can be chosen.
-
 Font size
Font size
-
The user can change the font size of a selection by typing the number of a different font size or by clicking on the little arrow to the right of the entry box and selecting the preferred size.
-
 Bold
Bold
-
Change the style of the current cell or the currently selected text to be bold, or unbold it if it is already bold.
-
 Italic
Italic
-
Change the style of the current cell or the currently selected text to be italicized.
-
 Underline
Underline
-
Change the style of the current cell or the currently selected text to be underlined.
-
 Left justify..
Left justify..
-
Justify the contents of the cell to the left of the cell.
-
 Center
Center
-
Center the content of the cells.
-
 Right Justify
Right Justify
-
Justify the content of the cells to the right side of the cells
-
 Center across the selection
Center across the selection
-
Center the content of the cells on the selected cells.
-
 Merge Cells
Merge Cells
-
Merge the selected cells into a single cell.
-
 Split Merged Cells
Split Merged Cells
-
Split previously merged cells into separate cells.
-
 Money
Money
-
Sets the format of the selected cells to be monetary.
-
 Percentage
Percentage
-
Sets the format of the selected cells to be a percentage.
-
 Thousands separator
Thousands separator
-
Sets the format of the selected cells to use thousands separator.
-
 Increase the displayed precision.
Increase the displayed precision.
-
Increases the number of decimals shown in the currently selected cell.
-
 Decrease the displayed precision.
Decrease the displayed precision.
-
Decreases the number of decimals in the currently selected cell.
-
 Decrease the displayed indentation.
Decrease the displayed indentation.
-
This button decreases the indentation of selected elements.
-
 Increase the displayed indentation.
Increase the displayed indentation.
-
This button increases the indentation of selected elements.
-
 Change the display borders.
Change the display borders.
-
This button and drop down menu can be used to set the borders of all the cells in the selection.
-
 Set the Background Colour.
Set the Background Colour.
-
This button and drop down menu can be used to set the back ground colour.
-
 Set the Text Colour
Set the Text Colour
-
This can be used to change the colour of the text.
4.4.4. The Long Format Toolbar
The Long Format Toolbar
The Long Format Toolbar contains all buttons that the Format Toolbar (described in Section 4.4.3 ― The Format Toolbar) contains, except in a different order.
In addition, the Long Format Toolbar also contains the following buttons:
-
 Subscript
Subscript
-
Change the style of the current cell or the currently selected text to be subscripted.
-
 Superscript
Superscript
-
Change the style of the current cell or the currently selected text to be superscripted.
4.4.5. The Object Toolbar
The Object Toolbar.
-
 Box
Box
-
Insert a rectangular box containing optionally some text into the worksheet.
-
 Ellipse
Ellipse
-
Insert an ellipse or a circle into the worksheet.
-
 Insert a Frame.
Insert a Frame.
-
This button allows a user to insert a frame into a worksheet.
-
 Line
Line
-
Draw a line on the worksheet.
-
 Arrow
Arrow
-
Draw a line with an arrow head at one end.
-
 Insert a Checkbox.
Insert a Checkbox.
-
This button allows a user to insert a check box.
-
 Insert a radio button.
Insert a radio button.
-
This button allows a user to insert a radio button.
-
 Insert a button.
Insert a button.
-
This button allows a user to insert a button.
-
 Insert a Scrollbar.
Insert a Scrollbar.
-
This button allows a user to insert a scrollbar.
-
 Insert a Spinbutton Box.
Insert a Spinbutton Box.
-
This button allows a user to insert a spinbutton box.
-
 Insert a Slider.
Insert a Slider.
-
This button allows a user to insert a slider.
-
 Insert a List.
Insert a List.
-
This button allows a user to insert a list.
-
 Insert a Combo Box
Insert a Combo Box
-
This allows a user to insert a Combo Box.
4.5. Data Entry Area
Immediately above the grid of cells is the data entry area as shown in Figure 4-36.
This is a small area, which contains a current cell indicator, a button, a button, an button, and an entry area for detailed editing of the cell contents. These elements are explained individually below.
- 4.5.1. Current Cell Indicator
- 4.5.2. The Button
- 4.5.3. The Button
- 4.5.4. The Button
4.5.1. Current Cell Indicator
On the far left of the Data Entry area is the current cell indicator area. This area is shown in Figure 4-37
The cell indicator will show the address for the cell at the top left of the selected region. This address is listed in the standard column:row notation. The alphabetic part indicates the column of this top leftmost cell and the numeric part indicates the row of this top left cell. For instance, the cell which is over three columns and down two rows is designated:
C2
This designation matches the column and row headers for this cell.
While a region is being selected, the current cell indicator will change to show the size of the region which is being selected. This information is presented in a row number by column number format. For instance, this designation:
15R x 6C
4.5.2. The Button
The Cancel button can be used to cancel the current edit and to restore the cell contents to the previous state. If a user decides in the middle of an edit that the data being entered into a cell is not what they want, the user can push this cancel button to cancel the current data and return the cell to the state it was at before.
The most common use of this button is when overwriting the contents of a cell with new data. If the user decided to revert the change before confirming it, the cancel button is the answer. Note that this button works just like typing the escape key on the keyboard.
4.5.3. The Button
The confirm button . can be used to finish the edit of a cell and enter the edit into the workbook. Note that this button works in the same way as the enter key.
4.5.4. The Button
The equals button can be used to start a formula in the currently selected cell. If a user wanted to make cell D10 equal to cell B4, the user could simply click on cell D10, click this equals button, click on cell B4 and type the enter key. Note that this button works the same way as the equals key.
4.6. The Cell Grid
Most of the work done on a spreadsheet is done to the main Cell area, the large grid like part of the worksheet. This is where all the formulas and data are entered, and is the center of activity for the spreadsheet.
Figure 4-38 shows the cell grid area, the column and row headers on the top and left, the scrollbars on the right and bottom and the tab list at the very bottom.
The figure has a few and shows that cell B3 as being selected. In this figure, the columns and rows have been resized and therefore look uneven.
Each cell in this area is delimited by a light grey line by default. The current selection is indicated by a rectangular box with a little box on the lower right, this case cell J12. The view in this figure shows the middle portion of a worksheet which is evident in two ways. Firstly, the column and row headers do not start at column A and row 1. Secondly, the scroll thumbs are not at the top and left. The thumbs are the boxes within the scroll bars that are used to scroll. Note also that cell D19 has a comment within it which is shown by the little red triangle at the top right corner.
The size of a cell is determined by the width of the column and height of the row that the cell is in. The columns and rows can be resized by acting on the header relevant to the cell. The user must move the mouse pointer to the edge of the header which is either to the right or below the cell. With the mouse pointer in this position, the pointer will change to a set of opposite pointing arrows. The user must then drag this edge away from the top left corner. This takes a little practice.
The cell area is the core of Gnumeric. Therefore the manual explains the use of cells in much greater detail in a separate section. Interested users should read Chapter 5 ― Working with Data.
- 4.6.1. The Column and Row Headers
- 4.6.2. The Scrollbars
- 4.6.3. The Tabbed Sheet Indicator
4.6.1. The Column and Row Headers
The sheet is bordered by column headers on the top and row headers to the left. Columns are labeled alphabetically running horizontally across the top of the sheet as shown in Figure 4-39.
Rows are labeled along the left side of the worksheet. Each label is a different integer increasing downward. This is shown in Figure 4-40.4.6.2. The Scrollbars
The cell grid area's scrollbars work like other scrollbars. In this case they let the user work on a worksheet which is much bigger than what could be shown at any given moment.
4.6.3. The Tabbed Sheet Indicator
At the bottom of Figure 4-38, Gnumeric has a tabbed sheet indicator. This is the boxes with the labels "Guppies", "Turtles", "Mermaids", "seahorses" and so on. In workbooks where there are more than one sheet, extra tabs are used to indicate how many sheets are there, and also allows the user to move to another sheet by clicking the proper tab. Each tab is a link to a separate worksheet within Gnumeric. In this figure, the "Turtles" tab has been selected. Gnumeric shows this by making the "Turtles" since the tab is a little bigger and making it overlap the two neighbouring tabs.
On the far right, the two arrows indicate that there are more sheets in the workbook and more tabs for those sheets. Unfortunately, there is not enough space to show them all so Gnumeric displays these arrows. If all the sheets are visible, these arrows will not be displayed. These arrows can be used to scroll the tabs and bring tabs that were hidden into view. This may be a little difficult to understand and work with but becomes easier quickly.
4.7. The Information Area
The section at the very bottom of the worksheet view is the information area as is shown in Figure 4-41.
The information area displays information depending on what is happening in Gnumeric.- 4.7.1. The Menu Hint Area
- 4.7.2. The File Status Indicator
- 4.7.3. The Running Calculation Area
4.7.1. The Menu Hint Area
The leftmost portion of the information display area, the part which reads: "Sort the selected cells" is a hint explaining what a menu does. In this case, the Data menu was opened and the pointer is hovering above the "sort" menu entry. Gnumeric is responding by giving a quick explanation of what that menu entry does.
4.7.2. The File Status Indicator
Whenever Gnumeric opens or saves a file, the file status indicator appears with a progress bar which grows as Gnumeric progresses. In Figure 4-41, Gnumeric was just over halfway done opening a file.
4.7.3. The Running Calculation Area
In the bottom right hand corner, is an info area that shows some constantly calculated values. The default set is to show the Sum of all the currently selected cells.
There is a right click option that includes a few more options. This can include Sum, Min, Max, Average, Count.
4.8. The Mouse Pointers used by Gnumeric
The shape of the mouse pointer (the pointer which is movable by the mouse) changes in different contexts. This indicates that different functionality is available and that mouse clicks will have different results. The different mouse pointers and the actions they indicate are discussed below.
-
 The left pointing arrow pointer:
The left pointing arrow pointer:
-
The left hand pointing arrow pointer is the standard pointer used for most of the interaction with Gnumeric. This pointer is used to select menus and menu entries, toolbar buttons, columns or rows, the scrolling `thumbs' and various other elements.
-
 The cell selection pointer:
The cell selection pointer:
-
This pointer appears over the cell grid area and can be used to select cells for editing.
-
 The text editing pointer:
The text editing pointer:
-
The text editing pointer is used to indicate the location in the text where new edits will appear. This cursor can be used to change the scale of the zoom, to change the name and size of the font currently used or to edit the cell contents in the cell entry area (the white area to the right of the equals (=) sign.
-
 The cross hair pointer:
The cross hair pointer:
-
The cross hair pointer can be used to change the cell selection area. The pointer appears when the mouse pointer is placed over the handle box, the black square at the lower right hand side of the selection. When the cross hair pointer appear, the selection can be altered by clicking the left-hand mouse button and dragging the handle to a new position. The cross hair pointer can also be used to insert a graphic object, by clicking with the left hand mouse button to place one corner and releasing the button to place another of the corners.
-
 The expansion pointers:
The expansion pointers:
-
These pointers can be used to change the height of rows or the width of columns. These pointers appear in certain dialog windows to resize the different parts of the dialog. The pointers are also used to resize graphical objects as is explained below.
-
 The sheet selection and hyperlink pointer:
The sheet selection and hyperlink pointer:
-
This pointer appears above the sheet tabs and can be used, by left clicking, to change the currently selected sheet or, by right clicking, to obtain the sheet dialog box. This pointer also appears above cells which are hyperlinks. Left clicking on a hyperlink may change the view to a new location, or may open an external file.
-
 The right pointing arrow pointer:
The right pointing arrow pointer:
-
The right hand pointing arrow pointer is used to select graphical objects (such as drawing objects (e.g. arrows, ellipses) and graph objects (e.g. charts)).
-
 The movement pointer:
The movement pointer:
-
The movement pointer can be used to move graphical objects around a worksheet without resizing the object.
-
 The graphical object re-sizing pointers:
The graphical object re-sizing pointers:
-
These pointers allow the resizing of graphical objects. If the mouse pointer is placed over one of the handle boxes of the graphical object, the handle box will turn green and the pointer will change to one of these forms. When these pointers appear, click dragging with the left mouse button will resize the graphical object either scaling or stretching the object.
-
 The window resizing pointers:
The window resizing pointers:
-
These pointers are used to change the size of Gnumeric windows and dialogs.
5. Working with Data
This chapter explains the core functionality of Gnumeric including the basic types of data manipulated by Gnumeric, the methods of entering, manipulating and formatting data, and the basic tools for analysis of these data. More advanced analysis is described in Chapter 6 ― Advanced Analysis.
- 5.1. Data in Gnumeric Cells
- 5.2. The Types of Cell Elements
- 5.3. Data Entry
- 5.4. Advanced Data Entry
- 5.5. Obtaining Data from External Sources
- 5.6. Selecting Cells and Cell Ranges
- 5.7. Moving and Copying Data
- 5.8. Deleting Data
- 5.9. Inserting New Data Cells
- 5.10. Formatting Cells
- 5.11. Conditional Formatting of Cells
- 5.12. Filtering Data
- 5.13. Modifying Data
- 5.14. Generating Data
- 5.15. Comments in Cells
- 5.16. Hyperlinks
- 5.17. Defining Names
5.1. Data in Gnumeric Cells
The purpose of a spreadsheet is to manipulate data and perform calculations on those data. In order to understand how to use Gnumeric, it is necessary to understand what types of data are available and how these types can be manipulated.
Because all of the data which are entered into a Gnumeric workbook can eventually be stored in a file, the file contents define the kinds of data which can be entered into the spreadsheet. A file contains:
- metadata about the file contents,
- global data for the workbook,
- the actual data contents of each worksheet in the workbook.
This chapter describes the information which can be stored in spreadsheet cells. This includes the five types of data which cells can contain and the formatting which can be applied to each cell. The chapter first describes the five data types available, then describes the formatting which can be performed on each cell, then explains how data can be inserted into a spreadsheet and finally describes how to copy and move data around a worksheet along with the transformations which can be performed as the data are moved. This chapter does not describe other types of data which can be stored in a spreadsheet such as drawing elements and graphs used to chart data. These are explained in later chapters.
5.2. The Types of Cell Elements
Each cell in a Gnumeric worksheet can contain only a single data element. These elements will have one of five basic types: text, numbers, booleans, formulas, or errors. During data entry, Gnumeric assigns a default data type to the cell based on an analysis of the cell contents. This assignment can be changed later if Gnumeric makes the wrong assignment. For information on how to change the data type of a cell, see Section 5.10 ― Formatting Cells.
The five basic types of data which can be stored in a spreadsheet cell are:
- Text
-
A text element can contain a series of letters, numbers or other contents. For example, the first cell in a worksheet might contain the characters —This worksheet describes the company's income — which Gnumeric would interpret to be text. In order to distinguish text elements from number or formula elements, the text element may start with a single quote. For instance, if a cell contained only the three digits 345, Gnumeric would consider that to be the number three hundred and forty five. If this cell is intended to be a string, Gnumeric will store the cell as '345. The newline character cannot be entered directly but must be entered as Alt+Enter. For more information on entering and formatting text elements, see Section 5.2.1 ― Text Data Elements.
- Numbers
-
A number element can contain a series of digits (425) but may include specific text and formatting characters to indicate negative numbers (-345), decimal separator (34.0567), thousand separators (12,342), currency ($23), dates (21-10-1998), times (10:23) or scientific notation (2.3e12). Dates may include the names of months or their abbreviation. The currency, decimal separator and thousands separator symbols vary depending on the locale (the language and other location specific behaviour) to which Gnumeric has been set. See Section 13.5 ― Languages and Locales to understand how to change the locale. If you want a number to be displayed as a plain string without any number formatting, you can put a single quote (') before it. For more information on entering and formatting, numeric elements see Section 5.2.2 ― Number Data Elements.
- Boolean
-
A boolean element can contain one of two values: TRUE and FALSE. These are useful as inputs or outputs from formulas and for boolean algebra. More information on boolean data elements is presented in Section 5.2.3 ― Boolean Data Elements.
- Formulas
-
A formula is an instruction to Gnumeric which describes a calculation which should be performed automatically. These formulas can contain standard arithmetic elements but can also contain references to other cells. Calculations which depend on other cells are usually recalculated when the values of another cell changes. Formulas always begin with a special character — the equals sign (=). The commercial at symbol (@) can be used instead of the equals sign during data entry but Gnumeric will convert this to an equals sign. Alternatively, an entry which describes a calculation and which starts with either the plus (+) or minus symbol (-) will be converted to a formula starting with an equals sign. For a more complete explanation of formulas, see Section 5.2.4 ― Formula Elements.
A cell reference is the part of a formula which refers to another cell. For example, in the formula to add two cells =(A4+A1), both A4 and A1 are cell references. These references can be quite complex referring to cells in different worksheets or even in different files. See Section 5.2.4.3 ― Cell Referencing for a complete explanation of references.
- Error
-
An error element describes the failure to calculate the result of a formula. These values are rarely entered directly by a user but usually are the display given when a formula cannot be correctly calculated. See Section 5.2.5 ― Error Elements for a complete list of error values and their explanation.
A cell may display a series of hash marks (######). This indicates that the result is too wide to display in the cell given the current font setting and the current column width. When this occurs, the value in the cell can be seen in two ways. If the cell is selected, the value will appear in the data entry area (to the right of the equals button directly above the cell grid). Alternatively, the column containing the cell can be widened until the data contents become visible: select the whole column (by clicking on the column header) and choose .
- 5.2.1. Text Data Elements
- 5.2.2. Number Data Elements
- 5.2.3. Boolean Data Elements
- 5.2.4. Formula Elements
- 5.2.5. Error Elements
5.2.1. Text Data Elements
Text elements consist of an arbitrary sequence of characters or numbers entered into a cell. Because Gnumeric automatically recognizes certain sequences as numbers or formulas, certain sequences of characters (such as sequences containing only digits or a text element which starts with an equals sign) must be treated specially to have them considered text. In order to force any sequence to be considered text, the sequence can be started with an apostrophe symbol ('). Alternatively, the 'number' format of the cell can be specified to be 'text' before entering the characters, as explained in Section 5.10.1 ― Number Formatting Tab. Text elements are the simplest elements to enter into spreadsheet cells.
An example of a spreadsheet cell grid with cells containing text is given in Figure 5-1.
Valid text entries include simple words, whole sentences and even paragraphs.
To include a newline in a cell, a special key combination is required. A newline symbol can be inserted with the key combination of Alt+Enter.
5.2.2. Number Data Elements
Number data elements include a variety of data all of which are stored and manipulated by Gnumeric as numbers. This includes integers, decimal fractions, general fractions, numbers in scientific notation, dates, times, and currency values.
Data are recognized as numbers when they are entered, dependent on the format of the sequence of characters entered. Gnumeric attempts to intelligently guess the subtype of the data and match the data to an existing format for numbered data. If it matches a data format, Gnumeric will automatically assign the datum to a data type and associate an appropriate display format with the cell. The format recognition of Gnumeric includes a wide variety of data formats which are discussed in detail in Section 5.10.1 ― Number Formatting Tab.
Because Gnumeric automatically guesses the data type of a number being entered into a cell, this process may have to be over-ridden for certain types of data. For example, postal codes in the United States consist of a sequence of numbers which Gnumeric interprets as an integer. However, U.S. postal codes can start with a leading zero which Gnumeric discards by default. In order to override the default format, the number format of the cell must be specified before the entry of the data. This is explained in Section 5.10.1 ― Number Formatting Tab, below.
5.2.3. Boolean Data Elements
Cells can contain boolean data elements. These elements arise from Boolean logic which is a branch of mathematics. These elements are useful for manipulation of formulas.
Boolean values can be either "TRUE" or "FALSE". If these strings are entered into a cell, Gnumeric will recognize these as boolean values. These values can then be used in formulas. Certain formulas will also return boolean values.
5.2.4. Formula Elements
Formulas are the key to making a powerful spreadsheet. A formula instructs Gnumeric to perform calculations and display the results. These calculations are defined as a formula data elements. The power of these formulas arises because these formulas can include the contents of other cells and the results of the formulas are updated automatically when the contents of any cell included in the formula change. The contents of other cells are included using "cell references" which are explained below.
Any formula entered into a cell must follow a specific syntax so that Gnumeric can interpret the formula correctly. This syntax closely follows mathematical notation but also includes spreadsheet formulas, object names and cell references.
- 5.2.4.1. Syntax
- 5.2.4.2. Using Functions
- 5.2.4.3. Cell Referencing
- 5.2.4.4. Names
- 5.2.4.5. Array Formulas
- 5.2.4.6. Database Formulas
5.2.4.1. Syntax
Formulas are distinguished from regular data by starting with an equals sign (=) as the first character. Everything following this equals sign is evaluated as a formula.
To accommodate those more familiar with Lotus spreadsheets, Gnumeric recognizes the commercial at symbol (@) as the beginning of a formula and substitutes an equals sign. The plus and minus characters (+ and -) may also start formulas that involve calculation, but when used in front of a single number only indicate the sign of the number.
The simplest formulas just use the standard math operator and symbols. Addition, subtraction, multiplication, and division are represented by +, -, *, and /, just as you would expect. +,- can be placed in front of numbers to indicate sign, as well.
=5+5 returns 10.
=5-4 returns 1.
=-5 returns -5.
=5*5 returns 25.
=(5*5)+11 returns 36.
=(5*5)+(49/7) returns 32.
Formulas can result in error values in several instances. If a formula is entered incorrectly, Gnumeric will display a warning and allow either the formula to be corrected or will save the formula as text for editing later. If a syntactically correct formula results in a nonsensical calculation (for instance, a division by zero), then an error value will be displayed indicating the error.
5.2.4.2. Using Functions
Formulas can also contain functions which denote the use of standard mathematical, business, statistical, and scientific calculations. These functions take the place of any data element in a formula and can therefore be combined with the standard arithmetic operators described above.
These functions have the form:
where FUNCTIONNAME indicates the name of a function and ARGUMENTS indicates one or more arguments to the function. The function arguments are separated by commas (,).While the documentation generally refers to functions and to cells in capital letters, their use is not actually case sensitive.
Some examples of the use of functions are:
The arguments of the functions vary in number from none, as in the PI() function, to an unlimited number, as in the SUM() function, depending on the type of function.5.2.4.3. Cell Referencing
Formulas can include the displayed data from other cells. These contents are described as `cell references' which are names indicating that the contents of other cells should be used in the calculation.
Each cell in a spreadsheet is named by its column and row labels. By default, the column labels are letters and the row labels are numbers. The first cell, therefore, is called A1. One column over and two rows down from cell A1 is the cell B3. In a worksheet of the default size, the right most and bottom most cell is cell IV65536 which is the cell in column IV and in row 65536. An alternative cell reference notation uses numbers for both row and column identification. See Section 5.2.4.3.2 ― References using R1C1 Notation below for details.
The value of a cell can be used in a formula simply by entering its name where a number value would otherwise occur. For example, to have the data in cell B1 appear in another cell, enter =B1 into that cell. Other more complex examples include:
- 5.2.4.3.1. Absolute cell referencing
- 5.2.4.3.2. References using R1C1 Notation
- 5.2.4.3.3. Referencing multiple cells
- 5.2.4.3.4. Referencing cells on other sheets
- 5.2.4.3.5. Referencing cells on other files
5.2.4.3.1. Absolute cell referencing
Cells can be referenced in the default way (relative referencing), or by using absolute referencing. Absolute referencing means that when the cell is copied, the cell reference does not change. Normally, auto-filling a cell range or moving a cell will change its cell reference so that it maintains a relation to the original cell. Absolute referencing prevents these changes.
The difference between absolute and relative cell references only matters if you are copying or moving cells that contain cell references. For cells that are going to remain in place, both the relative and absolute references have the same result.
For example, if =A1 is the formula entered into cell B2, cell B2 will display the data in cell A1, which is one row up and one column left. Then, if you copy the contents of B2 to cell F6, cell F6 will contain the value from E5, which is also one row up and one column left.
For the copied cell to still refer to A1, specify absolute references using the $ character: $A$1 refers to cell A1, no matter where it is copied.
The format for absolute cell referencing is to use a '$' in front of the cell coordinate that you want to stay constant. The column, the row, or both can be held constant.
What happens when a given formula is entered into cell B2, then copied to other cells?
- =A1
-
=A1 is a normal, or relative, cell reference function. When =A1 is entered into cell B2, it refers to the value of data one cell up and one cell left from the cell with the reference. Therefore, if this formula were copied from cell B2 to cell C2, the value displayed in cell C2 will be the value of data in cell B1. Copied to cell R19, the formula will display the data in cell Q18.
- =$A1
-
In this case, the column value is absolute, but the row value is relative. Therefore, if =$A1 is entered into cell B2, the formula refers to the data in column A that is one row up from the current location. Copied to cell C2, the formula will refer to the data in cell A1. Copied to cell R19, it will refer to the data in A18.
- =A$1
-
This formula uses a relative column value and an absolute row value. In cell B2, it refers to cell A1 as the data in the cell one column left and in row 1. Copied to cell C3, the formula will display the data in cell B1.
- =$A$1
-
No matter where this formula is copied, it will always refer to the data in cell A1.
5.2.4.3.2. References using R1C1 Notation
From the submenu you can select R1C1 notation for a worksheet. This causes all cell references on the sheet to be shown as “RrCc”, where r is the row number and c is the column number. When R1C1 notation is selected, the column headers show numbers rather than letters.
When r and c are positive integers, as in “R1C1”, the reference is absolute. To produce a relative reference, enclose a number in square brackets; if the number is zero, it can be omitted along with the brackets. For example, “RC[-2]” refers to the cell two columns to the left in the current row, while “R[1]C1” refers to the cell in the first column of the next row down from the referencing cell. The second example combines a relative row reference with an absolute column reference.
5.2.4.3.3. Referencing multiple cells
Many functions can take multiple cells as arguments. This can either be a comma separated list, an array, or any combination thereof.
- 5.2.4.3.3.1. Multiple individual cells
- 5.2.4.3.3.2. Referencing a continuous region of cells
- 5.2.4.3.3.3. Referencing non-continuous regions
A comma separated list of cell references can be used to indicate cells that are discontinuous.

For functions that take more than one argument, it is often easier to reference the cells as a group. This can include cells in sets horizontally, vertically, or in arrays.
The ':' operator is used to indicate a range of cells. The basic syntax is upper left corner:bottom right corner.

5.2.4.3.4. Referencing cells on other sheets
It is possible to reference cells which are not part of the current sheet. This is done using the SHEETNAME!CELLLIST syntax, where SHEETNAME is an identifier (usually a sheet name) and CELLLIST is a reference to a cell or range of cells as described in the previous sections. If SHEETNAME contains spaces or other special characters, you must quote the whole name to allow Gnumeric to recognize it as a single name. See the examples below.
When the reference is to a range of cells, the worksheet name only needs to be given with the first cell reference. The ending cell of the range is assumed to be on the same worksheet if an explicit sheet name is not specified. Note, however, that “Sheet1!A1:Sheet3!C5” is a legitimate cell range description. It identifies a range three columns wide and five rows deep on each of the worksheets from Sheet1 through Sheet3. The preferred form of such a reference is “Sheet1:Sheet3!A1:C5”, which is the form Gnumeric will display if you subsequently edit the contents of a cell containing such a reference.
5.2.4.3.5. Referencing cells on other files
It is possible to reference cells in other files. The canonical form for these references is [filename]SHEETNAME!CELLLIST. The square brackets serve to quote filename, so you should use quotation marks only if they are actually part of the file name. Note that the sheet name must be present in references of this form.
5.2.4.4. Names
Names are labels which have a meaning defined in the spreadsheet or by Gnumeric. A name can refer to a numeric value, a string, a range of cells, or a formula. For details on defining and using names, see Section 5.17 ― Defining Names.
5.2.4.5. Array Formulas
It is periodically useful or necessary to have an expression return a matrix rather than a single value. The first example most people think of are matrix operations such as multiplication, transpose, and inverse. A less obvious usage is for data retrieval routines (databases, realtime data-feeds) or functions with vector results (yield curve calculations).
5.2.4.6. Database Formulas
Solely for compatibility with Excel and ODF files, Gnumeric supports various database functions: DAVERAGE , DCOUNT , DCOUNTA , DGET , DMAX , DMIN , DPRODUCT , DSTDEV , DSTDEVP , DSUM , DVAR and DVARP .
Since these functions are quite restrictive on the criteria that can be used, it is often easier to use array functions as described in Section 5.2.4.5 ― Array Formulas. Array functions are also useful in the case that a specific database function does not exist:
As shown in Figure 5-2, instead of using (the non-existing) function DMEDIAN one can use the alternative expression median(if(A1:A20="AA",B1:B20)) entered as an array function as described in Section 5.2.4.5 ― Array Formulas. Multiple conditions can be combined using multiplication to obtain AND and addition to obtain OR as in median(if((A1:A20="AA")+(C1:C20="BB"),B1:B20)). Using defined names as introduced in Section 5.2.4.4 ― Names for A1:A20 and B1:B20 can make this code very flexible and readable.
In this case we cannot use if(OR(A1:A20="AA",C1:C20="BB"),...) since the OR function would be applied to all 40 equality tests rather than each of the 20 pairs of equality tests.
5.2.5. Error Elements
Cells can display error values if the formula contained in the cell cannot be solved or if other anomalous conditions occur.
In Gnumeric all error values have names that start with #. 8 error values are standardized:
| Name | Normal Use |
|---|---|
| #DIV/0! | Division by zero occurred. |
| #N/A | Not applicable. This is the result of the =NA() formula. |
| #NAME? | An unknown function name or other name was encountered. |
| #NULL! | The result of specifying an intersecting range that in fact does not intersect. |
| #NUM! | A formula could not be evaluated because an invalid number was used as argument, for example =SQRT(-1) |
| #REF! | An invalid cell address or reference was encountered. |
| #UNKNOWN! | Usually the result of importing an unrecognized error from a different file format. |
| #VALUE! | A formula could not be evaluated because the wrong type of argument was used. |
5.3. Data Entry
There are several ways to add data into a spreadsheet. The simplest data entry technique involves typing the data into a spreadsheet by hand. This is usually necessary the first time that data are introduced into a computer. If the data already exist in a computer file of some kind, a simple way might exist to insert these data into a Gnumeric worksheet. If the data are in a text file, they can be inserted into a worksheet rapidly using the text conversion facilities. If data exist in a spreadsheet file of a different format, Gnumeric may be able to open the file and the data can then be copied where they are wanted.
This section explains how to enter data by hand into a spreadsheet. The techniques necessary to obtain data from other computer sources are explained in Chapter 14 ― Working with Files which deals with external data sources.
If the information being entered into Gnumeric cannot be interpreted correctly, Gnumeric will display an error message. The user may then be forced to edit the data before continuing. For example, a formula may be mathematically incorrect if the user has two operators in a row (e.g. =3+*4) and the dialog will give the user the chance to re-edit the entry or accept the entry as text rather than as a formula. When the formula is corrected, the leading apostrophe can be removed and Gnumeric will re-interpret the entry as a formula.
- 5.3.1. Data Entry by Editing Cells.
- 5.3.2. Entering Text Data
- 5.3.3. Entering Number Data
- 5.3.4. Entering Boolean Data
- 5.3.5. Entering Formulas
- 5.3.6. Entering Errors
5.3.1. Data Entry by Editing Cells.
The simplest method to place data in a spreadsheet involves selecting the location for the data, typing the data on a keyboard and then typing the Enter key to finish the input.
-
Select the cell where you want to enter data by clicking on it with the white cross cursor. This will place the thick `selection' box around that cell.
-
Type in the data or formula. The details of this step are presented below for each of the five types of data which can be entered.
-
Press the Enter key. This will complete the input and move the selection box down one cell which will then be able to receive further input.
At any time while entering the data and before the Enter is pressed, the user can cancel the data entry by typing the Esc key. This will return the spreadsheet to the selection mode and restore the contents previously in the selected cell.
Instead of the Enter key, other keys can be used to input the data in the current cell. These other keys will move the selection box to other locations than does the Enter key. The Tab key inputs the entry in the currently selected cell and then moves the selection box one cell to the right of the current cell. The arrow keys input the entry into the currently selected cell and move one cell in the direction of the arrow. The Enter key can also be used in conjunction with other keys. Typing the Shift+Enter combination will move the selection upwards after entry. Typing the Ctrl+Enter combination will re-select the currently selected cell.
- 5.3.1.1. Advanced Editing Mode
5.3.1.1. Advanced Editing Mode
After selecting the cell and initially entering the data, the user is in a limited editing mode. The main key for editing mistakes in this mode is the backspace key.
For a more complete set of editing options, especially for longer entries, there is an advanced editing mode. To enter the advanced editing mode, press the F2 function key or click on the editing region. The keyboard focus will then shift from the current cell to the editing region at the top of the worksheet. There, you can use cursor keys to position the cursor within the data in the cell, and have all of the capabilities of the data entry area available.
For example, you can use:
- Backspace
Delete the character to the left of the cursor.
- Cursor keys
Move the cursor appropriately.
- Ctrl+K
Delete to the end of the line
All the normal key bindings for GNOME application entry boxes also apply in the data entry box.
After finishing the data entry, pressing the Enter key will input the data entry and move the selection box downward just like for the simple editing mode.
5.3.2. Entering Text Data
Text can be entered by selecting a cell, typing the text and then typing the Enter key. Anything that is not interpreted to be a number, boolean, formula or error will be treated as a text field. To prevent Gnumeric from interpreting an entry as one of these other elements, a leading apostrophe can be added to force the entry to be text. Any entry, no matter what the contents, which starts with a leading apostrophe (') will be considered to be text.
Postal codes in the United States are series of five integers. By default, Gnumeric interprets these to be numbers. This interpretation means that the leading zeros used in the postal codes of the northeastern region will be lost by default. To retain these leading zeros, either the code should be entered with a leading apostrophe (e.g. '02917) or the cells should be formatted as text before data entry (see Section 5.10 ― Formatting Cells for an explanation of formatting).
5.3.3. Entering Number Data
Numbers can be entered like other items. First the cell in which the number should be entered must be selected, then a valid number must be typed in and finally the entry must be inserted using the Enter key. The valid formats for numbers are presented in Section 5.2.2 ― Number Data Elements.
5.3.4. Entering Boolean Data
A boolean can be entered by selecting the cell, typing the boolean (either TRUE or FALSE) and then typing the Enter key.
5.3.5. Entering Formulas
Formulas can be entered simply by typing a syntactically correct formula in a cell. The correct syntax for formulas is explained in detail in Section 5.2.4 ― Formula Elements. Formulas begin with an equals sign (=) and contain arithmetic symbols, functions with their arguments and cell references.
To enter a formula, first the cell must be selected, then the correct formula must be typed, and finally the Enter key must be typed.
If the formula entered into Gnumeric cannot be interpreted correctly, Gnumeric will display an error message giving the user the choice of re-editing the formula or saving the formula as a text field to be edited later. For example, a formula may be mathematically incorrect if the user has two operators in a row (e.g. =3+*4). If the formula is saved as text, when the formula is corrected the leading apostrophe must be removed. Gnumeric will then re-interpret the entry as a formula.
5.3.5.1. Shortcuts for including cell references and ranges in formulas
Formulas often include cell references or references to ranges of cells as arguments to functions. These references and ranges can be entered into a formula simply by typing in the proper syntax (see Section 5.2.4.3 ― Cell Referencing for more details). But manually entering in cell ranges is slow and cumbersome. In order to speed up the entry of these cell ranges, the mouse and the keyboard arrow keys can be used to select these cell ranges quickly.
When editing a formula, if the cursor is at a point where a cell reference or range would be appropriate, the reference or range can be selected using the mouse. If the mouse is used to click on a cell, the reference of that cell will be entered into a formula. Alternatively, if the mouse is used to drag a selection over a range of cells, that cell range will become part of the formula. The selected range will be highlighted by a border of moving black dashes, commonly called the "marching ants" border.
-
Begin entering a formula as you would normally. Stop at the point where a cell reference is appropriate. For example, example, type =exp(
-
Click on the cell you want to reference. Its reference will be entered into the formula.
-
To finish the formula, just type in the closing parenthesis. This will also "unselect" the region.
The mouse can be used to select a single cell, a continuous range of cells or several disjoint ranges of cells just like regular selections.
If entering lots of formulas or even just entering a few formulas, it is often quickest to use the keyboard to select cells and ranges of cells for use in formulas. Just as reaching a input point allows the user to select cells with the mouse, it is possible to use the keyboard to select cells. Just use the cursor keys and selection modifiers to create a selection.
-
Select a cell to enter a formula into. For example A1.
-
Enter a formula, but stop the cursor at a point where a cell reference is appropriate. For this example, =SUM(
-
Move the selection around with the cursor keys. Move the selection cursor to cell B1 to start the selection.
-
Hold down Shift and move the selection one cell over and one cell down. Cells B1,B2,C1,C2 should now be selected and the formula should show =sum(B1:C2
-
To finish the function, close the parenthesis. The cell should now show =sum(B1:C2). Press enter and the formula is entered.
To select a range of cell, hold Shift and move over the desired area.
To stop entering a selection or to start over, press Shift+Backspace
5.3.6. Entering Errors
Errors are almost never entered directly into a spreadsheet but usually arise from problems which Gnumeric encounters during calculations. A list of errors with their meanings is presented in Section 5.2.5 ― Error Elements.
In an unusual case where it is needed, an error can be entered by hand like the entry of other elements. First the cell must be selected, then the error must be entered (e.g. #DIV/0!) and finally the Enter key must be pressed.
5.4. Advanced Data Entry
This section describes advanced methods for data entry in Gnumeric. This includes techniques useful when adding large amounts of data, methods to automatically catch mistakes during data entry, using pre-defined templates to format data input, obtaining data from external sources and generating sequences of random numbers with defined distributions.
5.4.1. Entering Large Quantities of Data
It is sometimes necessary to enter large amounts of data by hand into a spreadsheet. To facilitate this work, Gnumeric provides several techniques to facilitate the entry of large amounts of data.
If data are to be entered into a series of rows or columns, this region can be selected ahead of time thereby modifying the behaviour of the data entry keys (the Enter, Tab and arrow keys).
-
Select the region with the mouse. For example, the region from cell C4 to cell E8 can be selected by clicking with the left mouse button on cell C4 and dragging the mouse cursor to cell E8. (More information on complex selections is presented below.)
-
Enter data by typing the data and the Enter key. If this is done repeatedly, the fifth time the Enter key is pressed, the selection will not move to cell C9 but will jump up to cell D4.
The Tab key can also be used instead of the Enter key to move sequentially through the selection.
5.4.2. Entering a Regular Sequence
It is often necessary to enter a regular sequence of numbers or a repeated sequence of text. Gnumeric provides several ways to input series and sequences of this kind.
The simplest way to fill a series with the same element repeated involves entering the element once and dragging the selection box to fill that element repeatedly. For example, the text "employee:" could be input into cell C2. That cell could then be selected. The selection box is a thick white rectangle which surrounds the cell. This selection box has a small white square at the bottom right hand corner. If the mouse cursor is placed above this square box, it changes to a thin cross. If the left hand mouse button is clicked and held, and the mouse dragged to cell C10, Gnumeric will automatically fill all of the cells with the identical string.
An alternative way to enter data into a region involves first selecting the region, then typing the value and finally typing the Ctrl+Enter key combination. This will fill the whole region with the identical value which was originally entered.
A similar method is available to fill sequences of integers. If the example just given was altered so that cell C2 had the number 14 and the Ctrl key was held during the dragging of the selection, Gnumeric will automatically fill the cells C2 to C10 with the series 14,15,16,...,22.
More complex series and sequences of data can be entered with a similar mechanism.
To do an autofill:
-
Enter a value into the first cell you wish to autofill. For example, the cell C2 could have the number "24" entered.
-
Enter a second value into the second cell you wish to autofill. This must be adjacent to the first cell. This sets the increment to use when autofilling the rest of your cells. For example, the cell D2 could have the number "28" entered.
-
Select both the cells just entered. At the bottom-right of the selection should be a small box. Your mouse cursor will change to a cross-hair when placed over the box. Press and hold on the box. Drag in the direction, either vertical or horizontal, you wish to increment and release when all the cells are filled. For example, selecting cells C2 and D2, then dragging the bottom right of the selection to cell I2 will fill the cells with the sequence from 24 to 48 with each increment being 4.
An alternative to the last step involves using the menus. Once the first two values have been input, the whole range to be filled can be selected using the mouse and then the selection can be made from the and . This will automatically complete the series in the selected region.
Gnumeric is able to increment several types of data beyond simple integers. The procedure is the same as described above but involves different starting values. Gnumeric can increment:
- Integers
-
1, 2, 3, etc.
- Natural Numbers
-
1.03, 2.05, 3.07, etc.
- Weekday Names
-
Monday, Tuesday, etc.
- Weekday Abbreviations
-
Mon, Tues, etc.
- Month Names
-
January, February, etc.
- Month Abbreviations
-
Jan, Feb, etc.
- Strings with Numbers
-
Item1, Item2, etc
- Dates
-
11/14/2001, 11/15/2001, etc.
Gnumeric supports incrementing the date by month, date, or year.
Note that, While Gnumeric will increment days of the month, if you do 11/14/2001 and 12/14/2001, it will recognize it as the same day of the month and increment the month so the next value would be to 1/14/2002 instead of the day difference.
Gnumeric can be explicitly told the cells to autofill as in the examples above, but it can also guess the number of cells to fill based on the length of an adjacent column or row. For example, if the cells B2 to B10 have information and cell C2 has the integer value "1", then selecting cell C2 and double clicking on the bottom rightmost box of the selection rectangle will fill the value "1" from cell C3 to cell C10.
5.4.3. Automatically Correcting Simple Mistakes
The entry of large amounts of data into a spreadsheet is tedious work which is prone to repeated mistakes. Gnumeric provides a tool to automatically correct commonly made simple mistakes. The corrections are configured and activated using the `AutoCorrect' dialog, available via in the menu.
- 5.4.3.1. Capitalize the Names of Days
- 5.4.3.2. Correct TWo INitial CApitals
- 5.4.3.3. Capitalize the First Letter of Sentences
5.4.3.1. Capitalize the Names of Days
If this correction rule is activated, the first letter of a name of a day is capitalized automatically. For example, if you type `monday', it is automatically replaced by `Monday'.
5.4.3.2. Correct TWo INitial CApitals
A common mistake is to hold down the shift key a little bit too long while typing initial letters. When it happens, you will get two initial capitals instead of one. If this correction rule is activated, the second letter of words beginning with two capital letters is automatically lowercased. For example, if you type `TOtal' into a cell it is replaced by `Total'. Note that if the word contains two capital letters only, it is not replaced.
It is possible to specify exceptions to this tool. For example, you do not want the tool to replace the word `PVbonds' when it is typed. To specify exceptions, type `PVbonds' into the ``Do not correct'' entry, and press ``Add'' button. Now the word should be included in the list of exceptions. To remove a word from the list, select the word and press the ``Remove'' button.
5.4.3.3. Capitalize the First Letter of Sentences
If this correction rule is activated, the first letter of a sentence typed into a cell is capitalized, if it is a lowercase letter in the first place. Only text that ends to a dot is considered a sentence.
It is possible to specify exceptions to this tool. For example, you do not want the tool to capitalize letters after acronym `i.g.'. To specify exceptions, type `i.g.' into the ``Do not capitalize after'' entry, and press ``Add'' button. Now the word should be included in the list of exceptions. To remove a word from the list, select the word and press the ``Remove'' button.
5.4.5. Generating Random Number Sequences
Use the random number generation tool to generate random numbers. This tool can generate random numbers from various probability distributions.
Specify the random distribution by selecting one of the items from the random distribution list. The following random distributions are supported: Discrete, Normal, Poisson, Exponential, Binomial, Negative Binomial, Bernoulli, and Uniform.
Specify the parameters of the selected distribution:
- Discrete Random Distribution
-
Specify the value and probability input range in the “Value and Probability Input Range:” entry box. The value and probability input range is a table consisting of two columns and any number of rows. The first column specifies the discrete random values and the second column the probabilities for them. The discrete random values do not have to be numbers, for example, strings will do as well. The sum of the probabilities in the second column should be one. For example, if you have the values A, B, C, and D in A1:A4 and values 0.1, 0.4, 0.2, and 0.3 in B1:B4, you would specify the value and probability input range to be A1:B4.
If the probabilities do not add to 1, they will be automatically scaled.
- Normal Random Distribution
-
Specify the mean and the standard deviation. The default values are 0 for the mean and 1 for the standard deviation.
- Poisson Random Distribution
-
Specify the lambda in the “Lambda” entry. Lambda is the average number of events in a unit time interval.
- Exponential Random Distribution
-
Specify b in the “b Value” entry.
- Binomial Random Distribution
-
Specify the probability of success (p) in the “p Value” entry and the number of trials (n) in the “Number of Trials” entry. The Binomial distribution is a discrete distribution in which the experiment consists of n identical trials. Each trial is independent of other the trials and has two possible outcomes, a success or a failure. The probability of success p is constant from one trial to another. The mean of a random variable that has a Binomial distribution is E(X) = np, and the variance is var(X) = np(1-p).
- Negative Binomial Distribution
-
Specify the probability of success p in the “p Value” entry and the number of failures r in the “Number of Failures” entry. Negative Binomial distribution is a discrete distribution in which the experiment consists of a sequence of independent trials. Each trial has two possible outcomes, a success or a failure. The probability of success p is constant from one trial to another. The experiment continues until r failures are observed, where r is fixed in advance. The mean of a random variable that has a Negative Binomial distribution is E(X) = r(1-p)/p, and the variance is var(X) = r(1-p)/p^2.
- Bernoulli Random Distribution
-
Specify the probability of success (p) in the “p Value” entry. p is a probability value between 0 and 1. The Bernoulli distribution has two random values 0 and 1, and p is the probability to observe value 1. The mean of a random variable that has a Bernoulli distribution is E(X) = 1(p) + 0(1-p) = p, and the variance is var(X) = p(1-p).
- Uniform Random Distribution
-
Specify the range of the continuous random variable with the “Between:” and “And:” entries. The default values for these entries are 0 and 1.
Specify the number of variables in the “ Number of Variables:” entry on the `Options' Page. This determines the number of columns of random values to be produced.
Specify the number of random numbers for each variable in the “Size of Sample: ” entry on the same page. This determines the number of rows of random values to be produced.
Figure 5-6 shows some example data and Figure 5-7 the corresponding output.
5.5. Obtaining Data from External Sources
Data are commonly obtained from external sources such as from other files, either in a spreadsheet format or in delimited text format, from other applications using the mouse to copy and paste data or from external applications such as databases or internet data streams.
5.5.1. Obtaining Data from External Files
Data which already exist in an external file can be imported into a workbook first by opening the file into a separate instance of Gnumeric and then by copying the relevant data into the desired worksheet.
Data contained in external files in the formats of several other spreadsheet applications can be opened by Gnumeric. Gnumeric can open files in Applix (TM) format, GNU Oleo format, Lotus 123 (TM) format, Microsoft Excel (TM) format, Multiplan (TM) format, OpenOffice Calc or StarOffice Calc (TM) format, Plan Perfect (TM) format, Quattro Pro (TM) format, sc and XSpread format or in the Xbase format.
Data contained in external text files which are formatted in well defined ways can also be opened by Gnumeric. Gnumeric can open files formatted in Data Interchange Format, formatted as HTML tables, or formatted in text formats such as comma separated values or tab delimited records. The opening of text format files is configurable by the user so that text files which contain data formatted in a wide variety of schemes can be imported correctly into Gnumeric. Obtaining data from these files is explained in detail in the section titled Section 14.3 ― Opening Files.
Data which are opened into a separate instance of Gnumeric can be copied and pasted into the current worksheet with the copy and paste commands as explained in Section 5.7.2 ― Cut, Copy and Paste.
5.5.2. Obtaining Data by Cut and Paste
Data can be obtained from other Gnumeric workbooks or other applications using the mouse to copy data and paste them into a worksheet. This is explained below in the section titled Section 5.7.4 ― Cut and Paste Between Gnumeric and Other Applications.
5.5.4. Getting Data from an Internet Data Stream
Gnumeric has been connected to external data sources such as stock quotation service data streams using an experimental plugin. This requires the ability to write programming code. Information on extending Gnumeric by developing plugins can be found in the section called Section 18.4 ― Writing New Plugins and the actual computer source code can be found in the directory gnumeric/plugins/sample_datasource/ of either a distribution of Gnumeric or in a code checkout from the revision control repository.
5.6. Selecting Cells and Cell Ranges
By selecting multiple cells at once, common operations can be performed on all the cells which have been selected. These operations include data entry, copying the cells, and multiple other operations .
Some operations cannot be done on selections of arbitrary shape. For instance, Gnumeric could not correctly reshape a worksheet following the deletion of a discontinuous group of cells therefore such an operation is not allowed. If users attempt an operation which cannot be performed, a warning dialog will appear.
- 5.6.1. Simple Selections
- 5.6.2. Selecting Multiple Cells
- 5.6.3. Advanced methods of Selection
5.6.1. Simple Selections
The simplest selection involves a single cell. In most cases, simply clicking with the left hand mouse button while the mouse cursor is over a cell will cause that cell to become selected.
The selected cell is indicated by a dark double line with a small square in the bottom right corner. The selected cell is the one that is currently in focus and will take any input for the keyboard.
To make a cell become the selected cell, simply move the white-cross cursor over the cell and press the left mouse button. There is one exception: When on a cell that contains a hyperlink, the mouse cursor changes from the white cross to a hand and clicking the left mouse button activates the link. In that case the cell can be selected by clicking the middle mouse button.
5.6.2. Selecting Multiple Cells
Several cells can be selected at once. When multiple cells are selected, the selected cells are indicated with a light, "baby" blue colour. When a single block of cells is selected, a double black line will surround the selection, and all cells except the first one to be selected will be shown in light blue.
- 5.6.2.1. Continuous selections
- 5.6.2.2. Discontinuous selections
5.6.2.1. Continuous selections
To make a continuous selection of cells, move the white cross mouse cursor pointer to the cell at one corner of the block of continuous cells, click and hold the primary mouse pointer on that cell, drag the pointer to the opposite corner of the block of cells and then release the mouse button. The block of cells will now be selected.
The arrow keys can also be used to select a continuous block of cells. To add cells in this manner, first select the cell in one corner of the cell block with the primary mouse button, then hold the Shift key and use the arrow keys to expand the selection block.
5.6.2.2. Discontinuous selections
A discontinuous group of cells can also be selected, by selecting cells or block of cells while holding down the Ctrl key. To select a discontinuous group of cells, first select a cell or a continuous group of cells as explained above, then click and hold down the Ctrl while selecting more cells. All of the cells which are selected while the Ctrl key is held down will be added to the selection. All selected cells will be displayed with a light blue colour. Cells can be added individually or as continuous blocks. This selection process is additive with each selected cell added only once so selecting cells twice or more simply adds those cells once to the selection.
5.6.3. Advanced methods of Selection
There are several ways to make selections using the keyboard keys directly. These may be quicker than using the mouse pointer. As explained above, the simplest of these uses the Shift and arrow keys to make a new selection.
To select an entire row of cells, press the combination of Shift+space keys. This is equivalent to pressing the row label button on the left side of the sheet.
To select an entire column of cells, press the combination of Ctrl+Space keys. This is equivalent to pressing the column label button on the top of the sheet.
To select the entire sheet, press the combination of Ctrl+A keys. This is equivalent to pressing the button in the top left corner of the sheet.
The following list summaries keyboard shortcuts which can be used to select large cell blocks.
- Shift+Arrow : Define selection with cursor keys.
- Ctrl+Arrow : Jump to the end of the current region.
- Alt+Space : Select current row.
- Ctrl+Space : Select current column.
- Ctrl+A : Select the entire sheet.
- Ctrl+/ : Select the array formula around the current edit position.
5.7. Moving and Copying Data
Data which have been entered once into a spreadsheet can be moved to new locations and possibly duplicated. The simplest way to do this involves dragging the selection box. A more advanced way involves a formal cut or copy operation and then a paste operation in the new location. The latter approach allows the data to be modified as they are pasted which can be extremely important.
Currently Gnumeric only supports copying, cutting and pasting of simple selections or continuous selections as described in Section 5.6 ― Selecting Cells and Cell Ranges. You cannot copy, cut or paste discontinuous selections.
It is frequently necessary to copy the results of complex calculations into a new location. This is done by selecting the data and using the command from the dialog. This is explained in Section 5.7.3 ― Paste Special below.
- 5.7.1. Simple Copy and Move
- 5.7.2. Cut, Copy and Paste
- 5.7.3. Paste Special
- 5.7.4. Cut and Paste Between Gnumeric and Other Applications
5.7.1. Simple Copy and Move
The easiest way to move or copy a cell or a group of cells is by selecting the cell or cells to be moved or copied, then using the mouse to drag the selection box to a new location.
-
Select a cell to move by clicking in it. You can also select a range of cells as described in Section 5.6 ― Selecting Cells and Cell Ranges.
-
Click mouse button on the border of the selection (anywhere except the autofill square in the bottom right corner). Use mouse button to move cells or Ctrl+ mouse button to copy cells.
-
Drag the selection to the new location.
-
Release the mouse button.
The selected cells will be copied or moved to the new location. This will move both cells' content and formatting. When copying, relative cell references in all formulas will change as described in Section 5.2.4.3 ― Cell Referencing; when moving, relative cell references will remain unchanged.
5.7.2. Cut, Copy and Paste
Another, more flexible, way to copy or move a selection is to use cut, copy, and paste operations. These operations allow the user to copy or move selected cells to the clipboard buffer and then paste the contents of the clipboard buffer to a different location or a different workbook.
- 5.7.2.1. Cutting a Selection to the Clipboard
- 5.7.2.2. Copying a Selection to the Clipboard
- 5.7.2.3. Pasting the Clipboard
5.7.2.1. Cutting a Selection to the Clipboard
To cut a cell or a selection to the clipboard, you should select a cell or range of cells as described in Section 5.6 ― Selecting Cells and Cell Ranges and then use one of the following methods:
- Use keyboard shortcut Ctrl+X.
- Choose from the menu.
-
Click on
 Cut button in the toolbar.
Cut button in the toolbar.
- Right-click on the selection and choose from the context menu.
Please note that the selection will remain in its current location until you paste it. If you want to delete a selection without pasting it to a new location, use command instead.
5.7.2.2. Copying a Selection to the Clipboard
To copy a cell or a selection to the clipboard, you should select a cell or range of cells as described in Section 5.6 ― Selecting Cells and Cell Ranges and then use one of the following methods:
- Use keyboard shortcut Ctrl+C.
- Choose from the menu.
-
Click on
 Copy
button in the toolbar.
Copy
button in the toolbar.
- Right-click on the selection and choose from the context menu.
5.7.2.3. Pasting the Clipboard
To paste the contents of the clipboard (i.e., previously cut or copied selection) to a new location, just click on a cell and use one of the following methods:
- Use keyboard shortcut Ctrl+V.
- Choose from the menu.
-
Click on
 Paste
button in the toolbar.
Paste
button in the toolbar.
- Right-click on the cell and choose from the context menu.
If you are pasting a selection which was copied to the clipboard buffer, all relative cell references in all formulas will change as described in Section 5.2.4.3 ― Cell Referencing. The selection remains in the clipboard buffer so that it can be pasted again. The original selection will remain outlined with "marching ants" border.
If you are pasting a selection which was cut to the clipboard buffer, all cell references in all formulas will remain unchanged. The original selection will be removed from the workbook and the clipboard buffer will be cleared.
5.7.3. Paste Special
All of the methods described above to move or copy data create identical copies of the original cells in the new location. This means that both the contents and the formatting of the original selection are copied to the new location and also means that any data present in the new location are deleted. It is frequently important either to alter the data before it is pasted or to merge the data in the new location with the data being pasted. The command enables this.
The command can act exactly like the command or may selectively paste the cell contents, the cell formats, the calculated values of the original cells rather than their contents. described in the previous section copies both contents and formatting of the original selection. If you need more options, use command.
The command can be accessed, after a selection has been cut or copied as explained above, in one of two ways. First, the location where the pasting should happen must be selected. The easiest way to do this is to select the single cell which will be at the top left hand corner of the region of pasted cells. Alternatively, the exact region into which the cells will be copied can be selected. After the selection is made, the command can be chosen from the menu or the context menu obtained by clicking with the right mouse button in the cell area of the spreadsheet.
The menu item opens a dialog with three categories. By default, acts as if it were the menu item.
The first set of choices allow the user to control the data pasted.The user can choose to limit the pasting to only the cell contents (no cell formatting is copied) or the opposite only cell formats copied (no contents). Furthermore, the user can insert the selection while transforming all the contents into values only. Formulas will be replaced by their values.
A second set of choices allows the user to perform simple mathematical operations during the paste. These operations use the current contents of the cells in the paste range and the contents of the clipboard. For example, if you are pasting a cell containing number 5 to a cell that currently contains number 10 and choose option Divide, the result will be 10/5=2. Choosing option None will just replace the previous contents of the cells by the contents of the clipboard buffer (this is the default behavior).
The final choices contains the following options:
- Transpose. This option will transpose the selection, i.e. interchange the rows and columns. Thus, a range with k rows and n columns will become a range with n rows and k columns, so that the firs row becomes the first column, and so on.
- Skip Blanks. This option prevents Gnumeric from taking any action for the cells in the selection that are blank. For such cells, the existing contents of the cells in the paste range will be kept.
5.7.4. Cut and Paste Between Gnumeric and Other Applications
Cut and paste commands described above allow copying and moving selections from one location in a spreadsheet to another, or between different spreadsheets. However, you can also use cut and paste to exchange information between Gnumeric and other applications, using so-called X clipboard which is shared by all graphical applications.
Whenever you cut or copy a selection in Gnumeric, it is placed both in Gnumeric clipboard and in X clipboard. In X clipboard, it is placed as text, with formulas replaced by their values and contents of different cells separated by spaces.
To paste the selection from X clipboard to an application, click with middle mouse button (if you have two button mouse, you can emulate the middle mouse button by pressing left and right buttons simultaneously). Most applications also allow pasting from X clipboard by using keyboard shortcut (usually Ctrl+V) or by choosing .
To paste a selection from another application to Gnumeric, place this selection in the X clipboard. Usually it is done by just selecting it with the mouse; some applications also allow you to use keyboard shortcut Ctrl+C, or choose . After this, you can paste it in Gnumeric by using command described above. This command will automatically paste the contents of X clipboard if Gnumeric's own clipboard is empty.
Pasting X clipboard in Gnumeric will automatically launch the Text Import druid which will assist you in importing the plain text contents of X clipboard into the spreadsheet. The Text Import druid is described in Section 14.4 ― Importing Text Files.
5.10. Formatting Cells
This section describes how to format the appearance of data in a cell. The section Section 5.11 ― Conditional Formatting of Cells describes a more advanced method of formatting where the depends on various conditions involving the current cell value and/or the values in other cells.
Cell formats allow you to only change the way cell data appears in the spreadsheet. It is important to keep in mind that it only alters the way the data is presented, and does not change the value of the data.
The formatting options allows for monetary units, scientific options, dates, times, fractions,and more. Positive and negative values can have different colors and formats for aiding in keeping track of values. There are also a large variety of date and time formats for virtually any time and date format one can think of. Formatting also allows you to set font, background color, and borders for selected cells.
Finally, advanced formatting options allow you to lock some of the cells so that their values cannot be changed, or restrict the range of values that can be entered in the selected cells.
To change the formatting of a cell or a selection, you can either use the Format Cells dialog which holds all of the formatting options or use specific formatting elements available as buttons on the Format Toolbar.
This dialog, shown in Figure 5-16, gives you access to all formatting options.
To launch this dialog, select the cell or range of cells you want to format (see Section 5.6 ― Selecting Cells and Cell Ranges for details on selecting cells) and then use one of the following methods:
- Use keyboard shortcut Ctrl+1 (this is number one, not letter l).
- Choose in the menubar.
- Click with the right mouse button on the cell grid area and choose from the context menu.
The Format Cells dialog contains tabs Number, Alignment, Font, Border, Background, Protection, and Validation. These tabs are described in detail in the subsequent sections.
To set one of formatting options, select the corresponding tab, choose the options you need, and click . This will apply the options you selected (in all tabs) and close Format Cells dialog. You can also click on to apply the and keep the dialog open, or on to close the dialog without applying changes.
Some of the most commonly used formatting options, such as font, background, and alignment, can also be accessed by using the buttons in the Format Toolbar. This toolbar is described in detail in Section 4.4.3 ― The Format Toolbar,
- 5.10.1. Number Formatting Tab
- 5.10.2. Alignment, Font, Border, and Background Tabs
- 5.10.3. Protection and Validation Tabs
5.10.1. Number Formatting Tab
This tab allows you to select the format for the cell's contents. You can select one of the many preset formatting styles which should be more than adequate for the vast majority of cases. If none of these meet the needs of the user, it is possible to create your own formats.
To use one of the preset formats, select the format category (such as Number or Date) by clicking on the corresponding radiobutton in the left side of the dialog. The right side of the dialog will show you how the selected cell would look with this format and give more options for the selected format.
The following is a list of all available format categories:
- General
A Swiss army knife of a format. It will attempt to display a value it the 'best' way possible. The choice of format depends on the size of the cell and Gnumeric guess of what 'type' of value is being displayed (number, date, time ...).
- Number
Displays numbers with 0-30 digits after the decimal place. Negatives can be displayed normally, within parentheses, or in red color. Optionally a delimiter can be added every third order of magnitude (thousand, million, ...). Both the decimal point and the thousands separator have internationalization support.
- Currency
Similar to Number, with the addition of a currency symbol. Currently known symbols include $, ¥, £, ¤ and the three letter abbreviations of all major currencies. By default, Gnumeric will use currency symbol and placement (before or after the number) appropriate for your locale.
- Accounting
A specialization of Currency which pays more attention to the alignment of negative numbers. It ensures that a small amount of space is prepended to positive numbers so that they align with negatives.
- Date
This category contains various formats for presenting dates. By default, Gnumeric will use date format appropriate for your locale (country and language setting). You can also choose one of many possible date formats shown in the list in the right side of the dialog. The following is an explanation of codes used in these formats:
Some date formats also include time using the codes explained below. Examples of date formatting are shown in Table 5-2.- d: day of month (one or two digits). Example: 9.
- dd: day of month (two digits). Example: 09.
- ddd: day of week. Example: Wed.
- m: month (number, one or two digits). Example: 3.
- mm: month (number, two digits). Example: 03.
- mmm: month (abbreviated name). Example: Mar.
- mmmm: month (full name). Example: March.
- mmmmm: month (first letter). Example: M.
- yyyy: year (four digits). Example: 1967.
- yy: last two digits of year. Example: 67.
- Time
This category contains various formats for presenting time of day. You can choose one of many possible time formats shown in the list in the right side of the dialog. The following is an explanation of codes used in these formats:
Sometimes it is necessary to display more than 24 hours, or more that 60 minutes/seconds without the values incrementing the display unit of the next larger measure (e.g., 25 hours instead of 1 day + 1 hour). To achieve this, use codes '[h]', '[mm]', and '[ss]'. Examples of time formatting are shown in Table 5-3.- h: hours.
- mm: minutes.
- ss: seconds.
- Percentage
Multiplies a value by 100 and appends a percent. Can be used with 0-30 digits after the decimal place.
- Fractions
Approximate the value with a rational number with either a specific denominator or with a maximum number of digits in the denominator.
- Scientific
Formats the value using scientific notation, e.g. 5.334 E 6 for 5,334,000. Allows up to 30 digits after the decimal place. No provision for controlling the exponent are provided at this time.
- Text
-
Treats numeric values as text. This will show a number with as much precision as available and will lose knowledge of whether it represented a date, or time.
TIPIf your workbook contains serial numbers, ID numbers or other similar entries, choose Text format for them. If you choose General or Number format, Gnumeric will remove leading zeros, so that 01124 will be shown as 1124.
- Custom
This category allows you to define your own format. This is only recommended for advanced users as it requires understanding of the codes internally used by Gnumeric for describing formats. To make it easier, this category provides a list of codes for all predefined formats so you can create our own format by modifying one of them rather than starting from scratch.
| Format | Sample | ||
|---|---|---|---|
| General | 36068.755 | ||
| m/d/yy | d/m/yy | 9/30/98 | 30/9/98 |
| m/d/yyyy | d/m/yyyy | 9/30/1998 | 30/9/1998 |
| d-mmm-yy | mmm-d-yy | 30-Sep-98 | Sep-30-98 |
| d-mmm-yyyy | mmm-d-yyyy | 30-Sep-1998 | Sep-30-1998 |
| d-mmm | mmm-d | 30-Sep | Sep-30 |
| d-mm | mm-d | 30-09 | 09-30 |
| mmm/d | d/mmm | Sep/30 | 30/Sep |
| mm/d | d/mm | 09/30 | 30/09 |
| mm/dd/yy | dd/mm/yy | 09/30/98 | 30/09/98 |
| mm/dd/yyyy | dd/mm/yyyy | 09/30/1998 | 30/09/1998 |
| mmm/dd/yy | dd/mmm/yy | Sep/30/98 | 30/Sep/98 |
| mmm/dd/yyyy | dd/mmm/yyyy | Sep/30/1998 | 30/Sep/1998 |
| mmm/ddd/yy | ddd/mmm/yy | Sep/Wed/98 | Wed/Sep/98 |
| mmm/ddd/yyyy | ddd/mmm/yyyy | Sep/Wed/1998 | Wed/Sep/1998 |
| mm/ddd/yy | ddd/mm/yy | 09/Wed/98 | Wed/09/98 |
| mm/ddd/yyyy | ddd/mm/yyyy | 09/Wed/1998 | Wed/09/1998 |
| mmm-yy | Sep-98 | ||
| mmm-yyyy | Sep-1998 | ||
| mmmm-yy | September-98 | ||
| mmmm-yyyy | September-1998 | ||
| d/m/yy h:mm | m/d/yy h:mm | 9/30/98 18:07 | 30/9/98 187:07 |
| d/m/yyyy h:mm | m/d/yyyy h:mm | 9/30/1998 18:07 | 30/9/1998 187:07 |
| yyyy/mm/d | 1998/09/30 | ||
| yyyy/mmm/d | 1998/Sep/30 | ||
| yyyy/mm/dd | 1998/09/30 | ||
| yyyy/mmm/dd | 1998/Sep/30 | ||
| yyyy-mm-d | 1998-09-30 | ||
| yyyy-mmm-d | 1998-Sep-3 | ||
| yyyy-mm-dd | 1998-09-30 | ||
| yyyy-mmm-d | 1998-Sep-30 | ||
| yy | 98 | ||
| yyyy | 1998 | ||
5.10.2. Alignment, Font, Border, and Background Tabs
- 5.10.2.1. Alignment Tab
- 5.10.2.2. Font Tab
- 5.10.2.3. Border Tab
- 5.10.2.4. Background Tab
5.10.2.1. Alignment Tab
This tab allows you to set horizontal and vertical alignment and justification options.
-
The standard default justification. Use right justification for numbers and formulas, and left justification for text strings.
-
Left justify all cell contents.
-
Center all cell contents.
-
Right justify all cell contents.
-
Fill the cell with the contents. This will repeat the cell's contents as necessary to fill the width of the cell.
-
For text, wrap long lines of text and left justify. For other formats, same as Left.
-
Centers the cell's contents so the middle of each line is aligned with the middle of other lines. This only works with multiple cells.
Left and Right justification options also allow you to specify indent from left (respectively, right) side of the cell. Indent is measured in multiples of the current font size: for font size 10, indent 4 means 40 pts.
-
Align the top of the cells contents with the top of the cell.
-
Center the cells contents vertically. Equally space between the top and bottom.
-
Align the contents of the cell with the bottom of the cell.
-
For text, wrap long lines and spread lines of text evenly to fill the cell. For other formats (or if the text contains no long lines), same as Bottom justification.
5.10.2.2. Font Tab
This tab allows you to change the font used for cells content.
To change cells font, select font family (such as Times, Helvetica, etc), style (Normal, Bold, ...) and size in points. You can also select font color and special effects such as underlining or strikethrough.Gnumeric allows you to use any of the fonts known to GNOME printing system, gnome-print. The same fonts are used for screen display and for printing, assuring that the printed document will look identical to the one you see on screen. Advanced users can refer to documentation for gnome-print package to find out more about adding fonts and font management in GNOME.
A quicker way to change the selected cells' font is to use Format Toolbar.
5.10.2.3. Border Tab
This tab allows you to choose the border for the selected cells. You can select one of many border styles (none, single line, double line,...) and colors. You can also have different borders on different sides of the cell.
To choose a border for a cell or a selection, select border style and color in the right side of the tab and click on the buttons corresponding to the sides of the cells in the left side of the tab. In addition to the buttons for left, right, top, and bottom sides, you also have buttons for drawing diagonal and reverse diagonal of the cell. (Strictly speaking, these cannot be called borders, but it is natural to put them in this tab.) The lowest row of buttons contains buttons and . Clicking on removes all borders from the cell; clicking on puts border on all sides of the cell or selection.Please note that for a selection of cells, the buttons will put borders on one of the sides of selection, not of individual cells. For example, clicking on button will put the border along the bottom of the selection, so only the cells in the bottom row will be affected. In addition for selections you have three more buttons in the bottom row: , , and . puts borders on all inside vertical borders in the selection; puts borders on all inside horizontal borders in the selection, and puts borders on all inside borders in the selection, both vertical and horizontal.
To remove an existing border from one of the sides of a cell or selection, click on the corresponding button again.
5.10.2.4. Background Tab
This tab allows you to change the background of selected cells. You can choose solid color or patterned background. A preview of the selected background will be shown in the right part of the tab.
To select a solid color background, select the color from Background Color drop-down box. You can use of the standard colors or define your own color by clicking on button.
To select a patterned background, choose the background color in Background Color section. After this, choose the pattern color and type in Pattern section. Please note that the pattern type buttons use black pattern on white background, regardless of the colors you have chosen.
To remove pattern, choose Solid pattern type (top left button, looking like a white square).
5.10.3. Protection and Validation Tabs
These two tabs are used to control user's access to cells and restrict values of data allowed in a cell. Unlike other formatting options, these two tabs have no effect on a cells appearance. These options are mostly used for writing templates and forms to be filled by others.
- 5.10.3.1. Protection Tab
- 5.10.3.2. Validation Tab
5.10.3.1. Protection Tab
This tab allows you to see and change cell protection in imported Excel workbooks. Cell protection has no effect in Gnumeric: you can edit cells whether or not they are marked as protected. However, Gnumeric keeps the protection setting of imported Excel workbooks. If you later save your workbook in Excel format, Gnumeric will save the protection information too. For more information about cell protection in Excel, please refer to Excel documentation.
5.10.3.2. Validation Tab
This tab allows you to set restrictions on allowed values of data in the cells. If you (or someone else) attempts to enter a data that does not meet the set criteria, a warning (or an error message, depending on the options set in this tab) will be shown.
This tab consists of two part. The first part, Criteria is used to set the criteria for the cell values. The second part, Error Alert, is used to choose the action when data entered does not meet the criteria.
To set the criteria for cell values, follow these steps:
-
Choose the type of data contained in the cells, using the Allow drop-down list.
-
Choose a condition that must be satisfied by the cells value, using Condition drop-down list. In these conditions, val stands for the cells value (for text, val stands for the length of text string) and min, max, and bound are constants that you need to specify.
-
Enter the values of constants used in condition. For example, if you chose condition min<=val<=max , you need to enter values of constants min and max.
After specifying the criteria, you need to specify how Gnumeric should respond to incorrect cell value. You can choose one of four possible actions from Action drop-down list:
- None
Accept invalid value without any warning. Equivalent to having no validation.
- Stop
Do not accept the invalid value. Show the user an error message which you need to specify (see below).
- Warning
Show the user a warning dialog, giving him a choice whether to accept or reject the invalid value. You need to specify the message to use in the warning dialog (see below).
- Information
Accept invalid values but show the user a warning dialog. You need to specify the message to use in the warning dialog (see below).
If you choose one of the options Stop, Warning, or Information, you must enter the message that will be show to the user in the error or warning dialog. Otherwise, the dialog will be empty so it will be completely useless. You need to enter the title (which will be used as the window title for the dialog window) and the message itself. For example, the values shown in Section 5.10.3.2 ― Validation Tab will produce the dialog shown in Figure 5-23.
5.12. Filtering Data
With data filters you can select a subset of rows in the worksheet that meet the given criteria. You can, for example, copy rows of a table containing sales of departments whose profit has been exceptionally high into a new sheet simply using a filter.
- 5.12.1. Auto Filters
- 5.12.2. Advanced Filter
5.12.1. Auto Filters
This section has not yet been written.
- Alt+Down Open the AutoFilter in the current cell.
- Down and Up Changes the selected item in an AutoFilter
- Home Select the first item [All] in an AutoFilter
- End Select the last item in an AutoFilter
- Enter or Alt+Up Apply the current entry in an AutoFilter list, and close the combo-box.
5.12.2. Advanced Filter
To use advanced filter, you should have a few blank rows available in your worksheet to be used as a criteria range. These rows should not overlap with the rows in the table to be filtered.
Now copy all the column labels from the table you want to filter into the first blank row in the criteria range. Below the criteria labels, you can now type the conditions you want to match for the particular label. For example, under a label `Profit' you could type `>=1000'. The tool selects only rows that match all the criteria.
It is possible to have many conditions for a single label. For example, you can select the departments whose profit is either very high or very low. To do this, type, for example, `<=0' below the `>=40000' condition.
To start the tool, select ``Advanced Filter'' from the ``Data'' menu. It brings you the advanced filter dialog. In the dialog, select the action you want to take.
``Filter in-place'' writes the new table in-place. Note that you will lose all the rows in the table that will not match the criteria. ``Copy to a new location'' copies the selected rows into the same sheet but into the specified cell range. Type the cell range into the ``Copy to'' entry if you want this action to happen. The other options let you to copy the selected rows into a new sheet or a new workbook.
You should then specify the cell range containing the table to be filtered in the ``List range'' entry. The cell range containing the criteria is specified in the ``Criteria range'' entry. If the original table contains duplicate rows, you may also want to specify the ``Unique records only''. If it is checked on, the filter removes all duplicates.
To start the tool, you can then click the ``OK'' button and you will get the new table.
5.13. Modifying Data
This section has not yet been written...
- 5.13.1. Searching for Data
- 5.13.2. Searching and Replacing Data
- 5.13.3. Sorting Data
- 5.13.4. Shuffling Data
5.13.4. Shuffling Data
With data shuffling tool you can shuffle data in a given cell range. The tool can be started by selecting ``Shuffle'' menu item in ``Data'' menu. In order to use the tool give the input range in which the data to be shuffled is stored. The tool is able to shuffle the contents of the whole cell range, or, also shuffle data according to rows or columns. The shuffling method is selected under the ``Input Range'' entry. For example, if your data is grouped by rows then select ``Shuffle Method'' ``Rows''.
The default output method is to shuffle in-place. The shuffled data can also be written into a new sheet, new workbook, or into an existing sheet by giving the output range. If you select the ``Autofit Columns'' option, the width of each output column is automatically fixed according to the size of data in it.
5.15. Comments in Cells
Each cell in a worksheet can have an associated comment. Comments are not ordinarily visible. Cells having associated comments are marked with a red triangle in the top right corner of the cell. If you move the mouse cursor over the red triangle, the cursor changes to the left-pointing arrow. If the cursor remains over the triangle long enough, a pop-up window appears, displaying the author's name and the text of the comment. The pop-up window is removed when the mouse cursor is moved off the red triangle.
To add a comment to a cell, first select the cell. Next choose from the Section 4.2.6 ― Insert Menu to open the dialog. If the cell already has an associated comment, Gnumeric instead opens the dialog, which is shown below. The only difference is that the dialog is initialized with the existing comment and it includes a line identifying the author of the existing comment.
To change the appearance of the comment text, select the text to be formatted, then click on one of the character attribute selectors above the comment text box. You can select italics, strike-through, character weight, and underlining. The italics and strike-through selectors toggle the character attributes, based on the first character of the selected text. For example, if the first character is italic, clicking on the italics selector removes the italic attribute from all characters of the selected text.
The arrows next to the weight and underlining selectors open menus from which you can select a weight or underline style. Selecting a weight or underline style applies it to the selected text and makes it the meaning of the associated selector. For example, if you select from the weight menu, the selected text is made light. If you subsequently click on the weight selector, the text selected at that time is also made light. The weights may not all be visibly different, depending on the font in use.
"Wrap in properties window" controls word wrap in the comment editing box just above it. By default, lines are broken at spaces between words to prevent a line from exceeding the width of the text box. Click on the check-box to toggle word wrap. Line breaks occur in the comment pop-up only where you place them explicitly by pressing Enter. Turning off word wrap lets you see how the comment will be displayed in the pop-up.
5.16. Hyperlinks
Each cell can have an associated hyperlink. A hyperlink permits the user of a spreadsheet to go directly to a particular cell or group of cells, to access another file on the local computer or on the web, or to send an email message to an address built into the link.
To add a hyperlink to one or more cells, first select the cells. Next choose from the Section 4.2.6 ― Insert Menu to open the dialog.
If the selection includes a hyperlink, the dialog is initialized from the existing link. If there is more than one hyperlink in the selection, the cell in the first row that has a hyperlink, and the first such column of that row, is used to initialize the dialog.
When you click on , the information in the dialog is attached to each cell in the selection, replacing any previously defined links. For any empty cells in the selection, the text of the link is set as the contents of the cell. For all cells in the selection, the cell format is modified to give the contents a distinctive color, and the text is underlined.
If the link location text box is empty when you click on , no hyperlink is created. Instead, if any cells in the selection have existing hyperlinks, those hyperlinks are removed. The distinctive format applied to links is not removed. For that reason it might be preferable to choose Clear ▶ Formats & Hyperlinks from the Section 4.2.4 ― Edit Menu to remove existing hyperlinks.
Gnumeric supports four types of hyperlink. The first element of the dialog, the menu, selects the type of hyperlink to be created. The dialog varies slightly, depending on the selected hyperlink type:
-
Internal Link: The second element of the dialog is a text box labeled "Target Range". You can enter a single range, with or without a worksheet name. To select the range from the worksheet, click on the button at the end of the "Target Range" line. This collapses the dialog to a single line and makes it possible to interact with the cell grid. Select the desired sheet tab, if necessary, then select the desired cells. When the selection is complete, click on the button at the end of the Target Range input box to open the full dialog again.
When an internal link is activated by clicking on the cell, the range of cells given by the link address becomes the current selection. The cell closest to A1 in the new selection becomes the active cell.
-
External Link: The second element of the dialog is a text box labeled "File". Enter the path to a file. You can also enter a Universal Resource Locator (URL) here; the URL is accessed as described for Web Link below.
When an external link is activated by clicking on the cell, Gnumeric launches an application to present the file, based on its apparent type. For example, "mypic.jpg" would be opened in an image viewer, while "myinfo.html" would be opened in a web browser.
-
Email Link: The dialog provides text boxes where you can enter the destination address and subject line for an e-mail message.
When an email link is activated by clicking on the cell, Gnumeric launches an e-mail client to send a message. The message is initialized with the destination address and subject specified in the dialog.
-
Web Link: Enter a Universal Resource Locator (URL) in the Web Address text box.
When the link is activated by clicking on the cell, Gnumeric launches an application to display the information at the specified URL, based on its apparent type. For a web address beginning with "http://" or "https://" the application is the default web browser.
When you move the mouse pointer to a hyperlink in the cell grid, a tool tip appears. The default tip shows the link address and instructions for activating the link or selecting the cell. To define a tip specific to the link, select the radio button next to "Tip", then enter the tip text in the text box. If the link-specific tip is selected and left blank, no tip is displayed when the mouse pointer is on the link.
5.17. Defining Names
Names are labels with a meaning defined in the spreadsheet or by Gnumeric. Names can be defined for a whole workbook or for just a single worksheet. A name can refer to a numeric value, a string, a range of cells, or a formula. A name can be used wherever its meaning could otherwise be used.
A name is a sequence of letters, digits, and underscore characters, beginning with a letter or underscore. A name cannot look like a cell identifier. For example, "D7" is not a permitted name, while "D_7" and "_D7" are permitted.
To define a name or modify the definition of an existing name:
- If you wish to define or modify a name for use within a single worksheet and it is not the current worksheet, click on the appropriate worksheet tab at the bottom of the Gnumeric window.
- Open the dialog by choosing from the Section 4.2.4 ― Edit Menu.
- Use the dialog to modify the defined names as desired. When your changes are complete, click on to close the dialog.
The dialog lists the names defined in the workbook, organized into two or more groups corresponding to the workbook, the active sheet, and the inactive sheets, if any. When the dialog is opened, only the names defined for the workbook and the active sheet are visible; the definitions for any inactive sheets are collapsed into a single line for each, identified by the sheet name. The definitions for the workbook or a sheet can be exposed or hidden by clicking on the arrow at the left end of the workbook or sheet line.
The second column of the dialog can show one of three icons. To define a new name, click on the plus sign in the row for the workbook or the active worksheet. Names defined under a worksheet name are visible only on that worksheet. Names defined for the workbook are visible to any worksheet that does not have its own definition of the name. Names are created as "<new-name>", which must be changed before the definition can be used. Click on the new line to select it, then click on the name field and type the new name, followed by the Enter key. When you press Enter, the name is fixed. Only its value can then be changed.
If the second column shows a minus sign, the line is for a user-defined name. Click on the minus sign to delete the definition of the name. If the second column shows a padlock icon, the definition is created automatically and cannot be modified from this dialog.
For user-defined names, the third column of the dialog contains a downward- or upward-pointing arrow. Click on the arrow to move the definition down to the worksheet or up to the workbook. This operation is not permitted if the moved definition would replace a name already defined for the destination. To do such a replacement, first delete the name in the destination, then move the definition.
The last column of the dialog shows the value defined for the name. When a new name is created, this field is initialized with an absolute reference to the currently selected cells. To modify a definition, click on the value field and edit it as desired, then press the Enter key. To define a string value, enclose it in quotation marks, for example, 'string one' or "string two". To specify a range of cells, use absolute references. Relative references change in meaning depending on the cell where they are used, which is unlikely to produce your intended result. You can define a name as a cell or range of cells by clearing its existing definition, if any, and then selecting the desired cell or cells on the cell grid. You can switch worksheets prior to selecting cells. The dialog continues to modify names defined for the workbook or the worksheet that was displayed when the dialog was opened. A reference created by selection in the dialog includes the worksheet name and uses absolute cell coordinates. That is, a selection would look like "Sheet1!$A$1:$B$24".
Below the display of defined names is a filter box. If the workbook or sheet contains many defined names, you can see a subset of the names by typing a partial name in the filter box and pressing Enter. All names that do not contain the entered string are omitted from the display. Differences of case are ignored. For example, if “real” were entered in the filter box, names such as "Real_Value" and "Surreal" would be displayed. When you press Enter in the filter box, contexts that contain no matching names are automatically collapsed. You may later need to manually expand the workbook line, for example, if the filter string is changed. If the line for the workbook or a worksheet begins with a right-pointing arrow, it contains names that pass the filter. Clicking on the arrow will change it to a downward-pointing arrow and make the names visible. To see all the defined names, clear the filter by clicking on the button at the right end of the filter box.
In addition to the names defined by the user, Gnumeric has some pre-defined names for useful elements:
- Sheet_Title: The name of the current sheet.
- Print_Area: The range of cells set as the sheet's print area; undefined if print area is not set.
6. Advanced Analysis
This chapter explains many of the advanced analytic tools available in Gnumeric including linear algebra calculations, the goal seek tool, simulation analysis, and scenarios.
- 6.1. Advanced Analysis in Gnumeric
- 6.2. Analysis using Complex Numbers
- 6.3. Goal Seek Tool
- 6.4. Simulation Analysis
- 6.5. Analysis using scenarios
6.1. Advanced Analysis in Gnumeric
There are several kinds of analysis which can be performed using the Gnumeric spreadsheet. These include statistical analysis and linear programming methods. These are described in this chapter.
6.2. Analysis using Complex Numbers
Complex numbers can be used in Gnumeric but, because they are not fundamental types, all the analysis must be done with functions.
6.3. Goal Seek Tool
Use Goal Seek Tool to search for a value of a single model variable that yields a given desired value of another single variable. For example, you can use the Goal Seek to find the break-even value for sales (the break-even is the amount of sales whose marginal revenue just covers the fixed costs and the profit is thus zero).
- 6.3.1. Using the Tool
- 6.3.2. Results
- 6.3.3. Desired Value in a Given Range
6.3.1. Using the Tool
First, select the ``Goal Seek...'' tool item from ``Tools'' menu. Specify the output variable cell (``Set Cell'') by typing the cell reference into the entry or by clicking the worksheet cell. If you are searching for the break-even point, for example, you should specify the cell reference of the profit calculation here.
Specify the desired result for the output variable cell into the ``To Value'' cell. In the search for the break-even, specify this to be zero.
Specify the input variable cell (``By changing cell'') by typing the cell reference into the entry or by clicking the worksheet cell. In the search for the break-even, specify the cell reference of the sales here. When you have done this, you may want to press the ``Apply'' button to start the tool.
6.3.2. Results
Gnumeric will systematically iterate the model by changing the input value to achieve the desired result, if possible. If goal seek was successful the tool displays the message ``Goal Seeking with cell __ found a solution''.
It is possible that Gnumeric does not find a solution that generates the desired result. There may not be such a solution for the model, or, it may be too difficult to find. For example, the mathematical function behind the calculation may have many non-continuous points.
6.4. Simulation Analysis
- 6.4.1. Introduction to simulation analysis
- 6.4.2. Setting up the simulation model
- 6.4.3. Running the simulation
- 6.4.4. Simulation output
- 6.4.5. Using SIMTABLE
- 6.4.6. Determining the number of iterations
6.4.1. Introduction to simulation analysis
A simulation is the imitation of the operation of a real-world process or system. The behavior of a system is studied by generating an artificial history of the system through the use of random numbers. These numbers are used in the context of a simulation model, which is the mathematical, logical and symbolic representation of the relationships between the objects of interest of the system. After the model has been validated, the effects of changes in the environment on the system, or the effects of changes in the system on system performance can be predicted using the simulation model. 2
Gnumeric includes a facility for performing Monte Carlo Simulation. Monte Carlo simulation involves the sampling of random numbers to solve a problem where the passage of time plays no substantive role. 3 In other words, each sample is not effected by prior samples. This is in contrast to discrete event simulation or continuous simulation where the results from earlier in the simulation can effect successive samples within a simulation experiment. The Monte Carlo simulation will be enabled through the use of the Random Number functions as described in ??? and the results presented along with statistics for use in analysis. 4
6.4.2. Setting up the simulation model
The remainder of this chapter will illustrate use of the simulation tool using an example from Banks et. al. 5 A classic inventory problem is the newsvendor problem. A newsvendor buys papers for 33 cents each and sells for 50 cents. Newspapers not sold are sold as scrap (recycled) for 5 cents. Newspapers are purchased by the paper seller in bundles of 10. Demand for newspapers can be categorized as “good,” “fair,” or “poor” with probability 0.35, 0.45 and 0.20 respectively, with each day's demand being independent of prior days. The problem for the newsvendor is to determine the optimal number of papers to purchase when the day's demand is not yet known.
The daily profit equation for the newsvendor is:
To set up the model, this example will use two tabs in Gnumeric, a tab labeled 'Profit' to calculate profit, and a tab labeled 'Demand Tables' to store the various tables needed to calculate the demand for any given sampling.
For the Profit tab, set up the profit tab as in Figure 6-1.
At the top of the Profit' tab, the Profit table will be entered . There are three variables: Sale revenue, Cost and Scrap value, and they take the per unit coefficients of 0.5, 0.33 and 0.05 respectively. Enter the coefficients in cells B13 through D13. In cells B12 through D12, enter the equations for sale revenue, cost and Scrap value that are in the list below. In cell E12, enter the equation for Profit
Next, we add the values for the decision variable, which is the amount purchased, and the amount sold.
- B12: =B13*min(B16,B20)
- C12: =C13*B16
- D12: =D13*max(0,B16-B20)
- E12: =B12-C12+D12
- B13: 0.5
- C13: 0.33
- D13: 0.05
- B16: 50
Sometimes, there is a need to try a number of different values for a single parameter. In Section 6.4.5 ― Using SIMTABLE the SIMTABLE function will be used to automate the use of a set of values for a parameter such as purchase quantity. For now, set the purchase quantity to 50 in cell C16.
Next, create the demand tables from which the demand will be generated. In the tab 'Demand Tables' enter the values of the probability in cells B4 through B6 (B4: 0.35; B5: 0.45; B6: 0.2). In cells C4, C5 and C6 enter the cumulative probability values (C4: 0.35; C5: 0.8; C6: 1) as shown in Figure 6-2.
- B4: 0.35
- B5: 0.45
- B6: 0.2
- C4: 0.35
- C5: 0.8
- C6: 1.0
The next table is the daily demand for newspapers based on the type of news day. The table Distribution of Newspapers Demanded is in cells A11 through D18 of the Demand Tables worksheet as shown in Table 6-1 and contains the daily demand distribution values. The cumulative distribution tables in cells A21 through G29, shown in Table 6-2 are derived values from the Distribution of Newspapers Demanded using values in the top Distribution of Newspapers demanded table.
| A | B | C | D | |
| 11 | Demand | Good | Fair | Poor |
| 12 | 40 | 0.03 | 0.1 | 0.44 |
| 13 | 50 | 0.05 | 0.18 | 0.22 |
| 14 | 60 | 0.15 | 0.4 | 0.16 |
| 15 | 70 | 0.2 | 0.2 | 0.16 |
| 16 | 80 | 0.35 | 0.08 | 0.06 |
| 17 | 90 | 0.15 | 0.04 | 0 |
| 18 | 100 | 0.07 | 0 | 0 |
| A | B | C | D | E | F | G | |
| 21 | Cumulative Distribution | Values | |||||
| 22 | Demand | Good | Fair | Poor | Good | Fair | Poor |
| 23 | 40 | 0.03 | 0.1 | 0.44 | 0 | 0 | 0 |
| 24 | 50 | 0.08 | 0.28 | 0.66 | 0.03 | 0.1 | 0.44 |
| 25 | 60 | 0.23 | 0.68 | 0.82 | 0.08 | 0.28 | 0.66 |
| 26 | 70 | 0.43 | 0.88 | 0.94 | 0.23 | 0.68 | 0.82 |
| 27 | 80 | 0.78 | 0.96 | 1 | 0.43 | 0.88 | 0.94 |
| 28 | 90 | 0.93 | 1 | 0.78 | 0.96 | 1 | |
| 29 | 100 | 1 | 0.93 | 1 |
When these values are entered, the final results will look like Figure 6-3.
Finally, back in the Profit tab, the demand data will be filled in through the use of references to the Demand Tables tab as shown in Figure 6-4.
In the following cells, enter the equations below in the 'Profit' tab:
- B17: =rand()
- C17: =if(B17<'Demand Tables'!C4,"Good",if(C19<'Demand Tables'!C5,"Fair","Poor"))
- B18: =rand()
- B20: =lookup($C17,$B23:$D23,$B24:$D24)
- B21: =E12
- B24: =lookup(Profit!$B18,'Demand Tables'!E23:E29,'Demand Tables'!$A23:$A29)
- C24: =lookup(Profit!$B18,'Demand Tables'!F23:F29,'Demand Tables'!$A23:$A29)
- D24: =lookup(Profit!$B18,'Demand Tables'!G23:G29,'Demand Tables'!$A23:$A29)
When done, the Profit spreadsheet will be setup with a profit equation, decision variables, and random events as shown in Figure 6-4. The rand() functions in cells C17 and C18 return a random value between 0 and 1, which are used by the lookup() functions in cells B20, B24, C24 and D24 to calculate a randomly determined daily demand. Next, this sheet will be used for analysis through the use of simulation.
6.4.3. Running the simulation
To run the simulation, from the Gnumeric toolbar, select Tools → Simulation. In the Risk Simulation dialog box that appears, the first tab is the Variables tab. There are two entries in the Variables tab: Input variables and Output variables (Figure 6-5).
Input variables are the cells which hold the functions based on random numbers of the type described in Section A.14. In this case, they are the cells B17 and B18 in the Profit worksheet, which hold the rand() function. Later, when the quantity purchased is a parameter set by the SIMTABLE function, cell B16 which holds the purchase quantity will be added to the range of input variables.
Output variables are the results of interest, or the dependent variable. In this case, the dependent variables are the demand and the profit, which are in cells B20 and B21.
The next tab is the Options tab . There are four settings in the options as shown in Figure 6-6.
The second pair of options are the number of iterations and the Max time. In a simulation, each iteration is the equivalent of a sample. A sample from a random distribution is taken for each of the input values (as specified in the Variables tab) and the resulting output value(s). The more iterations, the better the estimate of the output value. However, this also takes more time to run. A Max time value is specified in seconds where the simulation will end without output if an individual simulation takes longer than the Max time allotted. If this occurs (see Figure 6-7), the options are to either increase the Max time value, or decrease the number of iterations. A more drastic option is to change the model so that fewer calculations or samples of random numbers need to be made.
The next tab is the Summary. There are two boxes in this tab, the Simulation Summary and the Summary of results (see Figure 6-8). In simulation summary, there is a description of the simulation parameters.
Due to the random nature of the simulation, the output may vary between simulation runs).
- Simulations: Number of rounds as determined in the Simulation Options box.
- Iterations: Number of iterations in a single simulation round.
- # input variables: Number of random numbers sampled for each iteration.
- # output variables: Number of outputs recorded for simulation
- Runtime: Runtime of simulations in seconds.
- Run on: Date and time simulation was run.
In the summary of results window, there are summary statistics for each round of the simulation. If multiple rounds were done, the results of each round can be browsed by using the 'Prev. Sim.' and 'Next Sim.' buttons below the Summary of results box. For each output and input variable, the summary shows the Min, Average and the Max value across the iterations for that round of the simulation. Note that for the input variables, this shows the random number that is the average, max and min. If the statistics on intermediate values, such as a cost distribution, was desired, these intermediate values should be added to the list of output variables.
The last tab is labeled 'Output'. This tab identifies the location where the output table will be generated. There are two sets of options, first the Output Placement then Output Formatting as shown in Figure 6-9.
The default output placement is 'New sheet'. This will create a new sheet in the Gnumeric workbook labeled 'Simulation Report (1)', where '1' can be replaced with another number if a tab labeled 'Simulation Report (1)' already exists. The option 'New workbook' creates a Gnumeric workbook named 'Book2.gnumeric' with a tab labeled 'Simulation Report.'
The third option is to embed the output table into an existing worksheet. This is done by specifying the 'Output range'. Note that the output range must be large enough to include the entire table, including heading information. For a single round this requires 11 rows and 16 columns. For example, the range Profit!A24:P35 would contain the statistics for one round with the three input variables and two output variables. As input and output variables change, or the number of rounds of the simulation change, the number of rows required will change.
For output formatting, their are four options.
- 'Autofit columns' automatically makes each column long enough to include the largest entry in that column. Note that column 'A' in the resulting spreadsheet used to save run information such as date and time and is kept narrow.
- 'Clear output range' is in effect if the Output Placement option chosen is Output range. It clears the selected cells in the spreadsheet before putting the output table in its place.
- 'Retain output range formatting' retains formatting for cells such as number formatting.
- 'Retain output range comments' retains comments that have been placed in output cells. This is most useful when the input and output variables remained the same.
6.4.4. Simulation output
The simulation output provides statistics on the output and input variables for each round. The statistics are calculated over the iterations in a single round of the simulation. These statistics for each variable are:
- Variable type and name - input variables are labeled as '(Input)'.
- Min – Minimum value of variable among iterations of round.
- Mean – Arithmetic mean of variable among iterations of round.
- Max – Maximum value of variable among all iterations of round.
- Median – Median of variable among iterations of round.
- Mode – Mode value among iterations of round. For the input variable, this will be “#N/A”.
- Std. Dev. - Standard deviation of the variable.
- Variance – Second moment of variable.
- Skewness - Third moment of variable.
- Kurtosis – Fourth moment of variable.
- Range – Difference between min and max of variable among iterations of the round.
- Count – Number of iterations in round.
- Confidence (95%) - 95% confidence interval of value, centered on mean.
- Lower Limit (95%) - Lower limit of 95% confidence interval of the value, centered on the mean.
- Upper Limit (95%) - Upper limit of 95% confidence interval of the value, centered on the mean.
The output will include a heading, then a table for each round of the simulation. Judicious choice of output variables will also include any intermediate values of interest in the simulation in this table. Each row of the output table has statistics of the values of a variable over the iterations of the simulation as shown in Figure 6-10.
The output will be of the input variables and the output variables that were variables tab of the Simulation window . For the input variables, the output will be the statistics of the random variable used in modeling the input variables. For the output variables, the statistics will be of the output variable. These statistics, in particular the standard deviation and confidence interval, should be examined to ensure the simulation was at a precision adequate for the purpose. Some notes on how to use these statistics for refining the simulation design can be found in Section 6.4.6 ― Determining the number of iterations.
6.4.5. Using SIMTABLE
The SIMTABLE function is intended to change a variable in the simulation so that each round of the simulation can be used to evaluate a different scenario. This automates the use of simulation for what-if questions or to create a set of possible outcomes to a situation.
In this example, we will use the SIMTABLE function to find the optimal quantity of newspapers to buy. For the purchase quantity in our spreadsheet, we will replace '50' with the following formula in Profit!B16:
Profit!B16 = SIMTABLE(50,60,70,80,90)
Each entry in the list of the SIMTABLE arguments is a value that will be used for the purchased quantity. Each entry corresponds to one round of simulation, as used in Figure 6-6. In this example there are 5 entries to the SIMTABLE list, so '5' will be entered into the 'Last Round #' option in the Options tab of the Simulation dialog.
When this simulation is run with 5 rounds, the summary of results will have one entry for each round, with each round using a different entry from the SIMTABLE function for the purchase quantity. The results for the various rounds can be previewed using the 'Prev. Sim.' and 'Next Sim.' buttons. The output also has one table for each round of the simulation.
As seen in Figure 6-11, each value in the original SIMTABLE statement corresponds to a simulation round, with the Purchase Quantity taking on the value from the SIMTABLE list. The analyst can then record the Profit statistics (mean, variance, skewness, kurtosis, 95% confidence intervals) and determine if the simulation results are of sufficient resolution for the analysts purposes.
The use of SIMTABLE to change parameters within the simulation provides a convenient method to do what-if analysis, and analyze the results as a whole.
6.4.6. Determining the number of iterations
In simulation, one major question is how many iterations are needed to reach a chosen level of precision in the results. Simulation as a tool provides an approximation of the actual relationship between the input and output variables. The precision of the approximation is based on the number of iterations of the simulation done. More iterations in the sample lead to greater precision. But the relationship between iterations and precision depends on the relationship between the variables in the precision. In addition, the analyst must decide which output variable is the variable of interest, and what degree of precision is required. The next step is to determine a sufficiently large number of iterations R be used to satisfy:

Where Θ-hat is the estimate of the mean, Θ is the actual mean, ε is the specified error, and (1-α) is the probability that the estimate is within ε of the actual value (i.e. the (1-α) confidence interval). Common values of (1-α) are 95% and 99%. The Simulation Report from Gnumeric includes values for the 95% confidence interval as shown in Figure 6-10.
The general procedure is as follows:6
- Run simulation for a sample of R0 iterations. The default value in Gnumeric is 1000, set in the options tab of the Simulation menu, Figure 6-6.
- Take the sample variance S02 from the simulation output spreadsheet and determine the sample standard deviation S0 (see Figure 6-10).
- Using
zα/2
as the z-value of the
(1-(α/2))
percentile of the standard normal distribution, set the initial estimate of the number of iterations required as the smallest integer
R
such that
. Note that if R0 is small, it would be more appropriate to use the student's t-distribution of tα/2, R0 instead of zα/2 .Iterations required for simulation
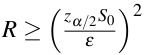
In this example, to estimate the profit to within ε=0.05 , first run the simulation with 1000 iterations and a purchase quantity of 50 results in the following
| Mean | Variance | Confidence (95%) | |
| Demand QUANTITY | 59.19 | 152.4 | 0.64 |
| Profit QUANTITY | 7.85 | 2.51 | 0.08 |
Taking the variance of the table, and setting ε=0.05 and α=0.05 , lookup zα/2 from a standard normal table. zα/2=1.96 so we have
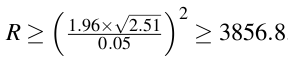
Therefore, the minimum number of iterations is 3857. The simulation can then be re-run with 3857 iterations to create a 95% c.i for profit where ε <=0.05 In this example with 3857 iterations, we get the following Simulation Report table:
| Mean | Variance | Confidence (95%) | |
| Demand QUANTITY | 59.11 | 163.9 | 0.34 |
| Profit QUANTITY | 7.72 | 2.88 | 0.04 |
As expected, the 95% Confidence interval for Profit is less than 0.05. For the newsvendor example, the next step would be to look at the confidence intervals of the profit for all values of purchase quantity, and verify that this confidence interval is adequate for the decision to be made.
7. The Solver
This chapter explains the linear programming solver available from within Gnumeric.
- 7.1. Solver
7.1. Solver
With Gnumeric Solver you can solve linear programs.
- 7.1.1. Introduction to Linear Programming
- 7.1.2. Spreadsheet Modeling
- 7.1.3. Using Solver
- 7.1.4. Integer Programming
7.1.1. Introduction to Linear Programming
A linear program (LP) is a problem that can be expressed as linear functions. As you probably already know, a linear function is the one whose graph is always a straight line. Thus each variable of it appears in a separate term with its coefficient. There must be no products or quotients of these variables. In addition, the exponent of each term must be one. No logarithmic, exponential, trigonometric terms are allowed. Especially note that functions like ABS, IF, MAX, and MIN are not linear. Here are a few examples of linear functions:
3x + y - 5z
-3.23x + 0.33y
-0.3x + 4y - 2z + 1.2m
The linear problem has a so called objective function which is to be minimized or maximized and constraints. The objective function is the one whose value we would like to optimize. Typically, this function could determine the profit generated by the expected sales of the given model (maximization problem), or, the cost of the production in the given environment (minimization problem). Anyway, on purely mathematical point of view, we could examine the following objective function:
Maximize 2x + 3y - z
In linear programming the variables of this functions are not allowed to take any values (otherwise the maximum of any objective function would be infinity). The problem also has constraints. The constraints are a set of linear functions and a set of their right hand side values (RHS). For example, for the previously defined objective function we have the following constraints:
x + y <= 5 (#1)
3x - y + z <= 9 (#2)
x + y >= 1 (#3)
x + y + z = 4 (#4)
x, y, z >= 0 (non-negativity assumption)
This constraint set consists of three inequality constraints (#1-#3) and one equality constraint (#4). Their RHS values are 5, 9, 1, and 4. In addition, we also have the non-negativity assumption. That is, all the variables (x, y, and z) have to take only positive numbers. The idea is to find the optimal values for the variables (x, y, and z) but also to satisfy all the given constraints.
7.1.2. Spreadsheet Modeling
To solve optimization problems with Gnumeric you have to type in the problem into a sheet. A recommended way to start with is to allocate a separate column in the spreadsheet for each decision variable (in the previous example the x, y, and z) and a separate row for each constraint (the constraints #1-#4). The coefficients of these variables should be placed into the cells corresponding to the allocated row and the column. It is also recommended that you label the rows and the columns to make the sheet much more readable. The sheet for our maximization problem would look like this:
As you can see, we have put the model variables into cells B3:D3. They are currently all zeros. The cell E4 contains the objective function definition. The easiest way to define it is to use SUMPRODUCT build-in function. Thus in our model, we have the formula `=SUMPRODUCT(B3:D3,B4:D4)' in E3.
The constraints are defined in rows seven to ten. Since the coefficients of these functions are in columns B, C and D we will get the total sum of each of the constraint using the formula `SUMPRODUCT(B$3:D$3,Bn:Dn)' where n is the row number of the constraint. For example, in E7 we have `=SUMPRODUCT(B$3:D$3,B7:D7)', in E8 `=SUMPRODUCT(B$3:D$3,B8:D8)' and so on. The right hand side (RHS) values of the constraints are typed into cells G7:G10.
7.1.3. Using Solver
- 7.1.3.1. Solver Parameters
- 7.1.3.2. Solver Constraints
- 7.1.3.3. Solver Reporting
- 7.1.3.4. Optimization
7.1.3.1. Solver Parameters
Now it is time to select `Solver...' from the `Tools' menu. After you have done it, the following dialog will appear:
Since we have the objective function in E3 type this into the `Set Target Cell:' entry. We are about to maximize this function, thus the radio button `Max' should be pressed on. By default, the problem is assumed to be maximization problem. The input variables (x, y, and z) were in cells B3:D3 so type the cell range into the `By Changing Cells:' entry.
The model to be optimized is a linear model. Thus, we should check that the check button `Linear (LP/MILP)' is pressed on the page `Model'. Also make sure that the assume non-negative button is on, otherwise, the input variables can also take negative values. There is also a check button `Assume Integer (Discrete)' which adds an integer constraint for all the input variables. The integer optimization is described, however, later.
A few additional options can be set too. If you want to limit the number of iterations the optimization algorithm is allowed to take you can set the maximum number in the `Max iterations' entry box on page `Options'. Similarly, you can limit the maximum time the optimization is allowed to take in the `Max time' entry box. If either one of these settings is exceeded during the optimization, the optimization is interrupted and an error dialog is displayed.
Some models can be better solved if the model is scaled into another form before the actual optimization. Gnumeric solver supports automatic scaling which can be checked on by using the check button on the bottom of the dialog. Note that the automatic scaling does not change the model since before checking out the results the model is scaled back to its original form.
7.1.3.2. Solver Constraints
Now we can add the constraints. Select the `Constraints' page from the top of the dialog and the following page should appear.
In this page, you can see all constraints that have been defined in the `Subject to the Constraints:' window. Since none has been defined, this window should be empty. Now type in the constraints (#1-#4) one by one.
When adding constraints, the three entry boxes in the bottom of the dialog are used. Put a cell name of the total left hand side (LHS) cell into the `Left Hand Side:' entry box. In our example, this would be E7 for the constraint #1, E8 for constraint #2, and so on. The combo entry in the middle defines the type of the constraint. It can be `≤', `=', `≥' ,`Int' or `Bool'. We will explain the `Int' and `Bool' constraints later. In this example, you should select `≤' for constraints #1-#2, `≥' for #3, and `=' for constraint #4. The last entry on the right takes the right hand side values of the constraints. For constraints #1-#4 they should be G7 (5), G8 (9), G9 (1), and G10 (4) in this order.
After typing a constraint press button, and you will be able to define the next one. When you have typed in all the constraints, the Solver dialog should look like this:
The order of the constraints does not matter. If you want to change or delete a constraint click it and then press `Change' or `Delete' button.
Note that you can also type ranges into the LHS and RHS entries. For example, you could have typed D7:D8 and G7:G8 instead of the two separate constraints.
If the constraints have now been typed in correctly, we should check what reports we want to produce.
7.1.3.3. Solver Reporting
Select the `Reports' page from the top of the dialog and you will see a checkbox named `Program'. This report gives the model in its mathematical form. Program report is useful for checking out the correctness of the model. It can also be useful for educational purposes.
7.1.3.4. Optimization
After you have specified the parameters, the constraints and the reporting options it is time to press the button. If everything went ok, you will see a dialog saying: `Solver found an optimal solution. All constraints and optimality conditions are satisfied.'. This means that the solver found an optimal solution and the optimal values are now stored into the input variables. For all models, this, however, does not happen.
If a feasible solution cannot be found, the solver reports that `A feasible solution could not be found. All specified constraints cannot be met simultaneously.'.
If the model is unbounded, the solver reports that `The Target Cell value specified does not converge! The program is unbounded.'.
If the maximum number of iterations specified in the options was exceeded, the solver reports that `The maximum number of iterations exceeded. The optimal value could not be found.'.
If the maximum time specified in the options was exceeded, the solver reports that `The maximum time exceeded. The optimal value could not be found in given time.'.
8. Statistical Analysis
This chapter explains the various statistical analysis tools available within Gnumeric including tools to create descriptive statistics, as well as parametric and non-parametric hypotheses tests.
Gnumeric includes various tools for statistical data analysis and data sampling. To use these tools select them from the Statistics menu and its submenus. The tools are described below. In this description as well as in the Statistics menu these tools are classified into six categories.
- 8.1. Overview
- 8.2. Descriptive Statistics
- 8.3. Sampling Tool
- 8.4. Dependent Observations
- 8.5. One Sample Tests
- 8.6. Two Sample Tests
- 8.7. Multiple Sample Tests
8.1. Overview
All tools have the same output options (see Figure 8-2). The results can be printed into a new sheet, into a new workbook, or into a given output range on a sheet of the current workbook. To select the output method select one of the radio buttons inside the Output frame. If you have chosen “” you must also enter a single range in the entry field.
Select the Autofit Columns option to automatically adjust the widths of the columns in the output range.
You will normally want to select the Clear Output Range option, since otherwise some of the cells with existing content will remain in the output range.
The Retain Output Range Formatting and Retain Output Range Comments options are useful if you have already preformatted the output range.
All analysis tools also provide a choice whether they will enter formulæ or just values in the cells. By default Gnumeric will usually enter formulæ. These formulæ will automatically reevaluate when the data change. For some tools, the formulæ also permit modification of certain parameters.
If the chosen output range is too small, some of the results will be lost.
The old data in the output range is deleted and cannot be recovered.
To enter a range into an entry field, you can either type the range specification into the text field, or click in the text field and then select the range on the sheet (see Figure 8-3).
Some entry fields accept lists of ranges. To enter these lists, select one range, type a comma, and then select the next range. At any time, you may switch to another sheet of the workbook.
8.2. Descriptive Statistics
- 8.2.1. Correlation Tool
- 8.2.2. Covariance Tool
- 8.2.3. Descriptive Statistics Tool
- 8.2.4. Frequency Tables
- 8.2.5. Rank and Percentile Tool
8.2.1. Correlation Tool
The correlation tool calculates the pairwise Pearson correlation coefficients of the given variables. Use this tool to calculate any number of correlation coefficients at the same time. The variables for which the correlations are calculated are specified by the “Input Range:” entry. The input range can consist of either a single range or a comma separated list of ranges. The given range or ranges can be grouped by columns, by rows, or by areas.
If the first row or column of the given ranges, or the first field of each area contains labels, the “” option should be selected.
For example, you want to calculate the correlation between three variables, one each in columns A, B, and C. Both variables have 10 values in rows 2 to 11 with labels in row 1 (see Figure 8-5).
- Enter A1:B11 in the “Input Range:” entry by typing this directly into the entry or clicking in the entry field and then selecting that range on the sheet. In the latter case the entry will also contain the sheet name.
- Select the “” radio button next to “Grouped By:”, since each variable is in its own column.
- Select the “” option since the first row contains labels. (see Figure 8-6).
- Specify the output options as described above.
- Press the OK button.
The calculated correlations are given in a table with each column and row labeled with the names of the variables. If the names are not given in the input range, Gnumeric generates them. In our example, the correlation between the variables in column A and B, can be found in the second column and third row of the results table (see Figure 8-7).
8.2.2. Covariance Tool
The covariance tool calculates the pairwise covariance coefficients of the given variables. Use this tool to calculate any number of covariance coefficients at the same time. The variables for which the covariances are calculated are specified by the “Input Range:” entry. The input range can consist of either a single range or a comma separated list of ranges. The given range or ranges can be grouped by columns, by rows, or by areas.
If the first row or column of the given ranges, or the first field of each area contains labels, the “” option should be selected.
For example, you want to calculate the covariance between three variables, one each in columns A, B, and C. Both variables have 10 values in rows 2 to 11 with labels in row 1 (see Figure 8-9).
- Enter A1:B11 in the “Input Range:” entry by typing this directly into the entry or clicking in the entry field and then selecting that range on the sheet. In the latter case the entry will also contain the sheet name.
- Select the “” radio button next to “Grouped By:”, since each variable is in its own column.
- Select the “” option since the first row contains labels.
- Specify the output options as described above.
- Press the OK button.
The calculated covariances are given in a table with each column and row labeled with the names of the variables. If the names are not given in the input range, Gnumeric generates them. In our example, the covariance between the variables in column A and B, can be found in the second column and third row of the results table (see Figure 8-10).
8.2.3. Descriptive Statistics Tool
The descriptive statistics tool calculates various statistics for the given variables and a confidence interval for the population mean. The variables are specified via the “Input Range:” entry. The given range or list of ranges can be grouped into variables by columns, rows, or areas.
This tool can produce four different kinds of statistical data.
-
If the “” option is selected, this tool calculates the mean, standard error, median, mode, standard deviation, sample variance, kurtosis, skewness, range, minimum, maximum, sum, and count for each variable.
-
If the “” option is selected, the tool calculates confidence intervals for the population mean of each variable. Specify the confidence level in the entry box. The default confidence level is 95%.
The interval given will usually be wider than the interval obtained using the CONFIDENCE function. The CONFIDENCE function assumes that the population standard deviation is known. This tool estimates the population standard deviation using the sample standard deviation.
If the “” option is selected, the tool finds the kth largest value of each of the variables. Specify k in the entry box next to the option. The default is 1.
If the “” option is selected, the tool finds the kth smallest value of each of the variables. Specify k in the entry box next to the option. The default is 1.
If the first entry for each variable contains the label, select the “” option.
Figure 8-12 shows some example data, Figure 8-13 the selected options, and Figure 8-14 the corresponding output.
8.2.4. Frequency Tables
Gnumeric provides two types of frequencies tables:
- The frequency table tools is primarily useful for non-numeric data (data of nominal and ordinal level of measurement). It allows to determine frequencies for given values.
- The histogram tool is useful for numeric data that is supposed to be classified into a certain number of intervals. These intervals can be either specified or calculated.
- 8.2.4.1. Frequency Tables Tool
- 8.2.4.2. Histogram Tool
8.2.4.1. Frequency Tables Tool
- 8.2.4.1.1. Introduction
- 8.2.4.1.2. The “Input” Tab
- 8.2.4.1.3. The “Categories” Tab
- 8.2.4.1.4. The “Graphs & Options” Tab
- 8.2.4.1.5. Frequency Tool Results
8.2.4.1.1. Introduction
The frequency tool can be used to create frequency tables for non-numerical data. It presents this table numerically as well as graphically.
If your data are numeric and you want to accumulate whole intervals of values into frequency counts then this tool is not appropriate. In that case you may want to use the histogram table tool described in section Section 8.2.4.2 ― Histogram Tool.
As shown in Figure 8-15, the frequency table dialog has four tabs. We will introduce them in sequence.
8.2.4.1.2. The “Input” Tab
The “Input” tab shown in Figure 8-15 contains the field specifying the data to be used for the histogram.
The “Input Range” entry contains a single range or a list of ranges, that can be grouped into variables by rows, columns, or areas.
If the first row or column of the given input ranges, or the first field of each area contains labels, the “” option should be selected. If the input is grouped by areas and the top left cell contains a label, the other cells in the first row are being ignored.
8.2.4.1.3. The “Categories” Tab
The “Categories” tab permits the specification of a range that contains the possible values that are supposed to be counted in the input range.
The “Automatic categories” option is disabled since it is not yet implemented.
8.2.4.1.4. The “Graphs & Options” Tab
The “Graphs & Options” tab allows various options to be set. In the top half of the tab you can choose whether you would like a graph to be created. If you choose to have a graph created you can specify whether you would like to see a bar chart or a column chart.
In the bottom part of the tab you can select the “percentages” option. This option replaces the frequency counts with percentages.
If the categories range contains repeated values, then the percentages may add up to more than 100%. If the categories range does not contain all values that occur in the input range, the percentages may sum to less than 100%.
The “Use exact comparisons” checkbox determines how category values and input range values are compared. If it is checked then the function EXACT is used for the comparison. If it isn't checked then simple equality is used. In this latter case, empty cells and cells containing the numerical value 0 are considered equal. As a consequence you usually want that checkbox to be selected.
8.2.4.2. Histogram Tool
- 8.2.4.2.1. Introduction
- 8.2.4.2.2. The “Input” Tab
- 8.2.4.2.3. The “Cutoffs” Tab
- 8.2.4.2.4. The “Bins” Tab
- 8.2.4.2.5. The “Graphs & Options” Tab
- 8.2.4.2.6. The “Output” Tab
- 8.2.4.2.7. A Histogram Example
8.2.4.2.1. Introduction
The histogram tool can be used to create histograms or frequency tables for numerical data. Using this tool you can define intervals, or “bins”. The tool determines how many data points belong to each bin and presents this number numerically as well as graphically.
If your data are non-numeric this tool is not appropriate. In that case you may want to use the frequency table tool described in section Section 8.2.4.1 ― Frequency Tables Tool.
As shown in Figure 8-19, the histogram dialog has five tabs. We will introduce them in sequence.
8.2.4.2.2. The “Input” Tab
The “Input” tab shown in Figure 8-19 contains the field specifying the data to be used for the histogram.
The “Input Range” entry contains a single range or a list of ranges, that can be grouped into variables by rows, columns, or areas.
If the first row or column of the given input ranges, or the first field of each area contains labels, the “” option should be selected. If the input is grouped by areas and the top left cell contains a label, the other cells in the first row are being ignored.
8.2.4.2.3. The “Cutoffs” Tab
The cutoffs for the histogram can either be predetermined by data contained in your workbook or calculated by the histogram tool. These cutoffs determine bins as defined by the selection on the “Bins” tab.
Select the “Predetermined Cutoffs” option to specify data on your worksheet in the “Cutoff Range:” entry. The values in this range will be used as cutoffs c1, c2, and so on to cn.
Select the “Calculated Cutoffs” option to have the cutoffs determined by the tool. Enter the desired number of cutoffs in the “Number of Cutoffs” entry. It is strongly recommended (but optional) that you specify the minimum and maximum cutoffs in the “Minimum cutoff” and “Maximum cutoff” entries. If the minimum or maximum cutoff is not specified, the tool will use the minimum and/or maximum of the current data.
8.2.4.2.4. The “Bins” Tab
The bins tab is used to determine how the cutoffs c1, c2, and so on to cn are translated into bins. Specifically, it has to be determined whether first and/or last bins reaching from −∞ to c1 and from cn to ∞ are added and whether data points that much cutoffs exactly are included in the bin to the right or the left.
For example the option “[∙,∙),[∙,∙),⋯, [∙,∙),[∙,∞) ” indicates that the first bin starts at the first cutoff while the last bin ends at ∞. Moreover, each cutoff value belongs to the bin on its right.
8.2.4.2.5. The “Graphs & Options” Tab
The options in the graphs and options tab specify any graph to be created and modify the appearance of the histogram:
-
The “” option causes the chart to be omitted.
-
The “” option causes a bar chart to be added to the histogram. For each bin, the bar chart shows a horizontal bar indicating the frequency.
The “” option causes a column chart to be added to the histogram. For each bin, the column chart shows a vertical bar indicating the frequency.
The “” option causes a histogram chart to be added to the histogram. For each bin, the histogram chart shows a vertical bar indicating the density (that is the frequency divided by the width of the bin).
-
The “” option causes the frequencies to be expressed as percentages.
-
The “” option causes a cumulative frequency table (either with counts or with pecentages) to be created.
-
The “” option determines whether only numbers are counted. If also non-numbers are counted they are first converted into numbers, usually into 0.
8.2.4.2.6. The “Output” Tab
The Output tab contains the standard output options and fields described in Section 8.1 ― Overview.
8.2.4.2.7. A Histogram Example
For example, you want to calculate a histogram for the number of successes in several sequences of trials. The numbers of successes are recorded in column A and the cutoffs of interest in column C (see Figure 8-23).
- Enter A1:A31 in the “Input Range:” entry of the “Input” tab by typing this directly into the entry or clicking in the entry field and then selecting that range on the sheet. In the latter case the entry may also contain the sheet name.
- Since you only have one variable select the “” or “” radio button next to “Grouped By:”.
- Select the “” option since the first cell of the Input Range contains a label.
- Enter C2:C5 in the “Cutoff Range:” entry of the “Cutoffs” tab. The “Predetermined Cutoffs” option will now also be selected (see Figure 8-24).
- In the “Bins” tab select the second option since we want to add two bins reaching to ∓∞ and we want to count each cutoff value in the bin to its right (see Figure 8-25).
- Select the “” option of the “Graphs &Options” tab to have the frequencies expressed as percentages.
- Select the “” option of the “Graphs &Options” tab to have a column chart added to the histogram (see Figure 8-26).
- In the “Output” tab, specify the output options as described in Section 8.1 ― Overview.
- Press the OK button.
The results are shown in Figure 8-27. Note that the graph will by default appear on top of the histogram table. It usually needs to be moved in to proper position. That has already been done here.
8.2.5. Rank and Percentile Tool
Use this tool to rank given data and to calculate the percentiles of each data point.
Specify the datasets to use in the “Input Range:” entry. The given range can be grouped into datasets by columns, by rows, or by areas.
For each dataset, the tool creates three columns in the output table:
- The first column gives the indices of the ordered data from largest to smallest data value.
- The second column gives data values corresponding to the indices in the first column.
- The third column indicates the percentile of the data value in the second column.
If you have labels in the first cell of each data set, select the “Labels” option.
Figure 8-29 shows some example data and Figure 8-30 the corresponding output.
In the case of ties, the rank calculated by this tool differs from the value of the RANK function for the same data. This tool calculates the rank as it is normally used in Statistics: If two values are tied, the assigned rank is the average rank for those entries. For example in Figure 8-29 the two values 10 are the second and third largest values. Since they are equal each receives the rank of 2.5, the average of 2 and 3. The rank function on the other hand assigns the rank as it is normally used to determine placements. The two values 10 would therefore each receive a rank of 2.
8.3. Sampling Tool

Use the sampling tool to take a sample of a data set. This tool can take both a random sample of a given size or a periodic sample:
- random sample
A random sample is a subset of the population such that every subset of that size has the same chance of being picked.
- periodic sample
In a periodic sample every kth element in the population is selected.
To use this tool, first specify the data set or data sets by setting the “Input Range:” entry. The range or ranges given can be grouped into datasets by rows, by columns, or by areas.
If the first entry in each data set contains a variable, select the “Labels” option.
Select the sampling method which can be either periodic or random.
- random sample
Specify the size of the random sample in the “Size of Sample:” entry.
- periodic sample
Specify the period in the “Period:” entry.
Specify the number of samples you would like to obtain in the “ Number of Samples:” entry.
Since the period uniquely determines a periodic sample, if you specify that you would like 2 samples you will be given the identical sample twice.
If the dataset for a periodic sample is a two dimensional range, Gnumeric will enumerate the data points by row first.
Figure 8-32 shows some example data and Figure 8-33 the corresponding output.
8.4. Dependent Observations
- 8.4.1. Forecast Tools
- 8.4.2. Fourier Analysis Tool
- 8.4.3. Kaplan Meier Estimates Tool
- 8.4.4. Principal Component Analysis
- 8.4.5. Regression Tool
8.4.1. Forecast Tools
- 8.4.1.1. Exponential Smoothing Tool
- 8.4.1.2. Moving Average Tool
8.4.1.1. Exponential Smoothing Tool
The Exponential Smoothing tool performs the exponential smoothing for the given set or sets of values. It provides the choice of 5 different exponential smoothing methods:
- Simple exponential smoothing according to (Hunter, 1968).
- Simple exponential smoothing according to (Roberts, 1959).
- Holt's trend corrected exponential smoothing (occasionally also referred to as double exponential smoothing)
- Additive Holt-Winters exponential smoothing
- Multiplicative Holt-Winters exponential smoothing (occasionally also referred to as triple exponential smoothing)
Since the kind of options available depend on the type of exponential smoothing desired, you can choose the type on the “Input ” page.
- 8.4.1.1.1. Common Options of the Exponential Smoothing Tool
- 8.4.1.1.2. Exponential Smoothing According to Hunter
- 8.4.1.1.3. Exponential Smoothing According to Roberts
- 8.4.1.1.4. Holt's Trend Corrected Exponential Smoothing
- 8.4.1.1.5. Additive Holt-Winters Method
- 8.4.1.1.6. Multiplicative Holt-Winters Method
8.4.1.1.1. Common Options of the Exponential Smoothing Tool
Specify the cells containing the datasets in the “Input Range” entry. The entered range or ranges are grouped into datasets either by rows or by columns.
If you have labels in the first cell of each data set, select the “Labels” option.
If you select the “Include chart” option, Gnumeric will also create a chart showing both the data and corresponding smoothed values.
8.4.1.1.2. Exponential Smoothing According to Hunter
Each value in the smoothed set is predicted based on the forecast for the prior period. The formula is given in Figure 8-35. α is the value given as “Damping factor”. yt is the tth value in the original data set and lt the corresponding smoothed value.
For example, a value for α between 0.2 and 0.3 represents 20 to 30 percent error adjustment in the prior forecast.
If you choose to have the tool enter formulæ rather than values into the output region, then you can modify the damping factor α even after you executed the tool.
To have the standard errors output as well, check the “Standard error” check box. The formula used is given in Figure 8-36. The denominator can be adjusted by selecting the appropriate radio button. Since there are t−1 terms in the sum of the denominator, selecting “n−1” means that the denominator will be t−2.
If you check the “Include chart” check box, a line graph showing the observations yt and the predicted values lt will also be created.
Figure 8-37 shows some example data, Figure 8-38 the selected options and Figure 8-39 the corresponding output.
8.4.1.1.3. Exponential Smoothing According to Roberts
The simple exponential smoothing method according to Roberts is used for forecasting a time series without a trend or seasonal pattern, but for which the level is nevertheless slowly changing over time. The predicted values are calculated according to the formula given in Figure 8-40. α is the value given as “Damping factor”. yt is the tth value in the original data set and lt the predicted value. l0 is the predicted value at time 0 and must be estimated. This tool uses the average value of the first 5 observations as estimate.
If you choose to have the tool enter formulæ rather than values into the output region, then you can modify the damping factor α and the estimated value at time 0 after executing the tool.
To have the standard errors output as well, check the “Standard error” check box. The formula used is given in Figure 8-41. The denominator can be adjusted by selecting the appropriate radio button.
If you check the “Include chart” check box, a line graph showing the observations yt and the predicted values lt will also be created.
Figure 8-42 shows example output for the exponential smoothing tool using the formula according to Roberts. Cell A4 contains the estimated level at time 0. If you requested to have formulæ rather than values entered into the sheet, then changing the estimate in A4 and/or the value for α in A2 will result in an immediate change to the predicted values.
8.4.1.1.4. Holt's Trend Corrected Exponential Smoothing
Holt's trend corrected exponential smoothing is appropriate when both the level and the growth rate of a time series are changing. (If the time series has a fixed growth rate and therefore exhibits a linear trend, a linear regression model is more appropriate.)
yt is the true value at time t, lt is the estimated level at time t and bt is the estimated growth rate at time t. We use the two smoothing equations given in Figure 8-43 to update our estimates. α is the value given as “Damping factor” and γ is the value given as “Growth damping factor”.
This tool obtains initial (time 0) estimates for the level and growth rate by performing a linear regression using the first 5 data values.
If you choose to have the tool enter formulæ rather than values into the output region, then you can modify the damping factors α and γ as well as the estimated level and growth rate at time 0 after executing the tool.
To have the standard errors output as well, check the “Standard error” check box. The formula used is given in Figure 8-44. The denominator can be adjusted by selecting the appropriate radio button.
If you check the “Include chart” check box, a line graph showing the observations yt and the estimated level values lt will also be created.
Figure 8-45 shows example output for Holt's trend corrected exponential smoothing. Cell A4 contains the estimated level at time 0 and B4 the estimated growth rate at time 0. If you requested to have formulæ rather than values entered into the sheet, then changing the estimates in A4, B4, the values for α in A2 and/or for γ in B2 will result in an immediate change to the predicted values.
8.4.1.1.5. Additive Holt-Winters Method
The additive Holt-Winters method of exponential smoothing is appropriate when a time series with a linear trend has an additive seasonal pattern for which the level, the growth rate and the seasonal pattern may be changing. An additive seasonal pattern is a pattern in which the seasonal variation can be explained by the addition of a seasonal constant (although we allow for this constant to change slowly.)
yt is the true value at time t, lt is the estimated level at time t, bt is the estimated growth rate at time t and st is the estimated seasonal adjustment for time t. We use the three smoothing equations given in Figure 8-46 to update our estimates. α is the value given as “Damping factor”, γ is the value given as “Growth damping factor” and δ is the value given as “Seasonal damping factor”. L is the value given as “Seasonal period”. If your data consist of monthly values, then L should be 12, if it consist of quarterly values then L should be 4.
This tool obtains initial (time 0) estimates for the level and growth rate by performing a linear regression using all data values. It obtains estimates for the seasonal adjustments by averaging the appropriate seasonal differences from values predicted by linear regression alone.
If you choose to have the tool enter formulæ rather than values into the output region, then you can modify the damping factors α, γ and δ as well as all estimates after executing the tool.
To have the standard errors output as well, check the “Standard error” check box. The formula used is given in Figure 8-47. The denominator can be adjusted by selecting the appropriate radio button.
If you check the “Include chart” check box, a line graph showing the observations yt and the estimated level values lt will also be created.
Figure 8-48 shows the options' tab of the exponential smoothing tool for the additive Holt-Winters method. The data is expected to have a seasonal period of 4 (this would for example happen if we have a data value for each quarter of a year). Figure 8-49 shows the corresponding example output for the additive Holt-Winters method. Cell C7 contains the estimated level at time 0, D7 the estimated growth rate at time 0, and E4 to E7 the initial seasonal adjustments for each of the 4 seasons preceding our data time period. If you requested to have formulæ rather than values entered into the sheet, then changing any of these estimates, the values for α in A2, for γ in B2 and/or for δ in C2 will result in an immediate change to the estimated values.
8.4.1.1.6. Multiplicative Holt-Winters Method
The multiplicative Holt-Winters method of exponential smoothing is appropriate when a time series with a linear trend has a multiplicative seasonal pattern for which the level, the growth rate and the seasonal pattern may be changing. A multiplicative seasonal pattern is a pattern in which the seasonal variation can be explained by the multiplication of a seasonal constant (although we allow for this constant to change slowly.)
yt is the true value at time t, lt is the estimated level at time t, bt is the estimated growth rate at time t and st is the estimated seasonal adjustment for time t. We use the three smoothing equations given in Figure 8-50 to update our estimates. α is the value given as “Damping factor”, γ is the value given as “Growth damping factor” and δ is the value given as “Seasonal damping factor”. L is the value given as “Seasonal period”. If your data consist of monthly values, then L should be 12, if it consist of quarterly values then L should be 4.
This tool obtains initial (time 0) estimates for the level and growth rate by performing a linear regression using the data values of the first 4 seasonal periods. It obtains estimates for the seasonal adjustments by averaging the appropriate seasonal differences from values predicted by linear regression alone during the first 4 seasonal periods.
If you choose to have the tool enter formulæ rather than values into the output region, then you can modify the damping factors α, γ and δ as well as all estimates after executing the tool.
To have the standard errors output as well, check the “Standard error” check box. The formula used is given in Figure 8-51. The denominator can be adjusted by selecting the appropriate radio button.
If you check the “Include chart” check box, a line graph showing the observations yt and the estimated level values lt will also be created.
Figure 8-52 shows the example output for the multiplicative Holt-Winters method, assuming 4 seasons. Cell C7 contains the estimated level at time 0, D7 the estimated growth rate at time 0, and E4 to E7 the initial seasonal adjustments for each of the 4 seasons preceding our data time period. If you requested to have formulæ rather than values entered into the sheet, then changing any of these estimates, the values for α in A2, for γ in B2 and/or for δ in C2 will result in an immediate change to the estimated values.
8.4.1.2. Moving Average Tool
Use the moving average tool to calculate moving averages of one or more data sets. A moving average provides useful trend information of the data that is lost in a simple average. In addition, moving averages can be used to eliminate random variance. For example, use this tool to create a smoother curve of a stock prize.
Specify the cells containing the datasets in the “Input Range” entry. The entered range or ranges are grouped into datasets either by rows or by columns.
If you have labels in the first cell of each data set, select the “Labels” option.
Choose the type of moving average you would like to calculate. The tool can determine 4 types of moving averages:
- Simple moving average
- Cumulative moving average
- Weighted moving average
- Spencer's 15 point moving average
Specify the “Interval” for the moving average. The interval i is the number of consecutive values to be included in each moving average. This options is only available for the simple and weighted moving averages.
Check the “Standard errors” checkbox if you would also like the standard error to be calculated. Since there is no general agreement on the denominator for the standard error you can choose the appropriate radio button.
In the case of the simple moving average, you can also choose between a prior moving average and a central moving average, or you may even specify any other desired offset.
- “Prior moving average”: Each average takes into account the current observation and the most recent prior observations for a total of i observations.
- “Central moving average” with i being odd: Each average takes into account the current observation and the same number of most recent prior observations and closest future observations for a total of i observations.
- “Central moving average” with i being even: This is calculated according to the formula given in Figure 8-55. at is the moving average at time t and yt is the observation at time t.
- “Other offset”: If the offset is 0, this is just the prior moving average. Otherwise the offset indicates the number of closest future observations to include in the average. Correspondingly, the number of most recent past observations is decreased.
The results are given in one column for each dataset (with a second column added if you have chosen standard errors to be calculated). Each row represents the moving average of the corresponding row or column in the input range. Depending on the type of average and the offset, the moving average cannot be calculated for the first rows in the input range.
- 8.4.1.2.1. Simple Moving Average
- 8.4.1.2.2. Cumulative Moving Average
- 8.4.1.2.3. Weighted Moving Average
- 8.4.1.2.4. Spencer's 15 Point Moving Average
- 8.4.1.2.5. A Moving Average Example
8.4.1.2.1. Simple Moving Average
A simple moving average is the unweighted average of a collection of observations. Exactly which observations are included depends on whether a prior or central moving average is calculated.
8.4.1.2.2. Cumulative Moving Average
A cumulative moving average is a prior moving average in which the current and all prior observations are included.
8.4.1.2.3. Weighted Moving Average
A weighted moving average with an interval i is a prior moving average calculated according to formula Figure 8-55. at is the moving average at time t and yt is the observation at time t.
8.4.1.2.4. Spencer's 15 Point Moving Average
Spencer's 15 point moving average is a central moving average calculated according to formula Figure 8-57. at is the moving average at time t and yt is the observation at time t.
8.4.1.2.5. A Moving Average Example
Figure 8-58 shows some example data, Figure 8-59 shows the option settings, and Figure 8-60 the corresponding output.
8.4.2. Fourier Analysis Tool
The Fourier Analysis tool normally performs a Fast Fourier Transform to obtain the discrete fourier transform Fs of the given sequence ft of real numbers according to the formula given in Figure 8-62.
Select the “Inverse” option to calculate the inverse discrete fourier transform ft of the given sequence Fs of real numbers
If the number of terms in the given sequence is not a power of 2 (i.e. 2, 4, 8, 16, 32, 64, 128, etc.), this tool will append zeros to reach such a power of 2!
Specify the cells containing the datasets in the “Input Range” entry. The entered range or ranges are grouped into sequences either by rows or by columns.
If you have labels in the first cell of each data set, select the “Labels” option.
Before using the numbers obtained by this tool, ensure that these are in fact the correct formulae for your discipline. In the physical sciences this fourier transform tends to be called the inverse fourier transform and vice versa. Moreover, frequently the scaling factor varies.
For example Mathematica uses the terms fourier transform and inverse fourier transform with the reversed meaning than Gnumeric and it uses a scaling factor of 1/SQRT(N) rather than 1/N.
8.4.3. Kaplan Meier Estimates Tool
- 8.4.3.1. The “Input” Tab
- 8.4.3.2. The “Groups” Tab
- 8.4.3.3. The “Options” Tab
- 8.4.3.4. The “Output” Tab
- 8.4.3.5. A Kaplan-Meier Example
8.4.3.1. The “Input” Tab
The “Input” tab shown in Figure 8-63 contains the fields specifying the data to be used for the Kaplan Meier Estimates. The time column contains the times or dates at which the subjects died or were censored. If any of the subjects were censored, the Permit censorship checkbox is checked and the Censor column contained the censorship marks. Censorship marks are typically 0s or 1s. The range of censor marks or labels can be set using the remaining two spinboxes.
8.4.3.2. The “Groups” Tab
If the subjects belong to several groups and the groups are supposed to be analyzed separately, the groups tab can be used.
The groups tab can be enabled via the Define multiple groups checkbox. The groups column entry contains the address of the column specifying the group membership. Groups can then be defined or deleted via the Add and Remove buttons.
8.4.3.3. The “Options” Tab
The options tab of the Kaplan-Meier tools dialog is used to set various options of the Kaplan-Meier tool.
8.4.3.4. The “Output” Tab
The Output tab contains the standard output options and fields described in Section 8.1 ― Overview.
8.4.3.5. A Kaplan-Meier Example
Suppose you want to calculate Kaplan-Meier Estimates for the as given in Figure 8-66. Each row contains the data for one subject. Column A contains the survival time, i.e. the time until death or censure. Column B contains the group number, we are considering two groups of subjects. Column C indicates whether the subject died (0) or was censured (1).
We complete the fields of the Input tab as shown in Figure 8-66. The time column is A2:A21 and the censure column is C2:C21.
Since we have two groups of subjects, on the Groups tab we check the Define multiple groups check box and set up two groups with identifiers 1 and 2 in column B2:B21:
On the Options tab all checkboxes are pre-checked and we leave them that way to obtain a maximum amount of information.
On the output tab we choose where we would like the output to be placed. For the purposes of this example we retain the New Sheet target. After clicking OK we get the output shown in Figure 8-68. Note that the graph initially always appears on top of the numerical result and was moved for the screen shot.
B1:F17 shows the results of the first group, G1 to K17 the results of the second group. The graph shows the Kaplan-Meier survival curves for both groups.
M4:N7 shows the result of the Mantel-Haenszel Log-Rank Test. In this case the p-value is larger than 0.3 and we would fail to reject the Null hypothesis. There is no evidence that the survival times differ.
8.4.4. Principal Component Analysis
Principal Component Analysis Tool performs a principal component analysis (PCA). PCA is a useful statistical technique with application in fields such as face recognition and image compression. It is a common technique for finding patterns in data of high dimension.
Specify the cells containing the datasets in the “Input Range” entry. The entered range or ranges are grouped into the factors either by rows or by columns.
If you have labels in the first cell of each factor, select the “Labels” option.
Suppose you want to perform a principal component analysis on the data given in Figure 8-70 having the two dimensions (factors) x and y.
- Enter Sheet1!$A$1:$B$11 (or just A1:B11) in the “Input Range:” entry by typing this directly into the entry or clicking in the entry field and then selecting the range on the sheet.
- Select the “” option since the first row contains labels. (see Figure 8-69).
- Specify the output options as described above.
- Press the OK button.
The output of this principal component analysis is shown in Figure 8-75. The output shows the covariance matrix, the eigenvalues and corresponding eigenvectors. The principal component is the constructed factor with the highest percent of trace, ξ1.
8.4.5. Regression Tool
The regression tool performs a multiple regression analysis.
Enter a range or list of ranges containing the independent variables into the “X Variables:” entry.
Enter a single range containing the dependent variable into the “Y Variable:” entry.
If the ranges for the independent and dependent variables also contains labels in the first field of each row, column or area, select the “ Labels” option.
Specify the confidence level in the “Confidence Level:” entry. The default is 95%.
To force the regression line or plane to pass through the origin, select the “Force Intercept To Be Zero” option.
Specify the output options as described above. If the output is directed into a specific output range, that range should contain at least seven columns and 17 rows more than there are independent variables.
Suppose you want to perform a regression analysis on the data given in Figure 8-73 using v and y as independent variables and u as dependent variable.
- Enter B1:C11 in the “X Variables:” entry by typing this directly into the entry or clicking in the entry field and then selecting the range on the sheet.
- Enter A1:A11 in the “Y Variable:” entry.
- Select the “” option since the first row contains labels. (see Figure 8-74).
- Specify the output options as described above.
- Press the OK button.
The output of this regression analysis is shown in Figure 8-75.
8.5. One Sample Tests
- 8.5.1. Normality Tests
- 8.5.2. One Median
8.5.1. Normality Tests
The normality test tool provides for four tests of normality.
- Anderson Darling Test
- Cramér-von Mises Test
- Lilliefors (Kolmogorov-Smirnov) Test
- Shapiro-Francia Test
The data range is specified via the “Input Range:” entry (see Figure 8-76). The given range or list of ranges can be grouped into separate data sets by columns, rows, or areas. The tool performs a separate test for each data set.
On the test tab one specifies which of the four tests to perform, the significance level for the test and whether to include a normal probability plot of the data (see Figure 8-77).
Suppose you want to perform a Lilliefors (Kolmogorov-Smirnov) Test for Normality on the data given in Figure 8-78.
- Enter A1:A50 (or Sheet1!$A$1:$A$50) in the “Input Range:” entry by typing this directly into the entry or clicking in the entry field and then selecting the range on the sheet.
- Select the “” option since the first row contains a label (see Figure 8-79).
- On the test tab of the dialog (see Figure 8-80) select the Lilliefors (Kolmogorov-Smirnov) Test.
- Specify an appropriate significance level Alpha, say 0.05.
- Select the “” option to include a normal probability plot in the output.
- Specify the output options as described above.
- Press the OK button.
The output of this normality test is shown in Figure 8-81. Note that the graph appears initially on top of the output data and needs to be moved to make the data visible.
8.5.2. One Median
The One Median test tool provides two non-parametric tests that test the null hypothesis that the sample comes from a population with a given median:
- Sign Test
- Wilcoxon Signed Rank Test
Selecting the appropriate submenu item opens the dialog with the respective test preselected.
- 8.5.2.1. Sign Test
- 8.5.2.2. Wilcoxon Signed Rank Test
8.5.2.1. Sign Test
This section describes the one sample sign test to test the null hypothesis that the sample comes from a population with the given median. The tool to perform a sign test to test the null hypothesis that two paired samples come from populations with the same median is in section Section 8.6.2.1 ― Sign Test.
The Sign Test tool performs a one-sample sign test whether the sample comes from a population with a given median.
The sample data range is specified via the “Input Range:” entry (see Figure 8-82). The given range or list of ranges can be grouped into separate data sets by columns, rows, or areas. The tool performs a separate test for each data set.
On the “Test”tab of the dialog (see Figure 8-83) the predicted median as well as the significance level are specified.
Suppose you want to perform a Sign Test on the data given in Figure 8-82 to determine whether the sample comes from a population of mean 3.
- Enter A1:A19 (or Sheet1!$A$1:$A$19) in the “Input Range:” entry by typing this directly into the entry or clicking in the entry field and then selecting the range on the sheet.
- Select the “” option since the first row contains a label. (see Figure 8-82).
- On the “” tab of the dialog (see Figure 8-83) select the Sign Test.
- Specify an appropriate significance level Alpha, say 0.05.
- Select thepecify the median of the null hypothesis (3) in the “” entry.
- Specify the output options as described above.
- Press the OK button.
The output of this sign test is shown in Figure 8-84.
8.5.2.2. Wilcoxon Signed Rank Test
This section describes the one sample Wilcoxon signed rank test to test the null hypothesis that the sample comes from a population with the given median. The tool to perform a Wilcoxon signed rank test to test the null hypothesis that two paired samples come from populations with the same median is in section Section 8.6.2.2 ― Wilcoxon Signed Rank Test.
The Wilcoxon Signed Rank TTest tool performs a one-sample sign test whether the sample comes from a population with a given median.
The sample data range is specified via the “Input Range:” entry (see Figure 8-82). The given range or list of ranges can be grouped into separate data sets by columns, rows, or areas. The tool performs a separate test for each data set.
On the “Test”tab of the dialog (see Figure 8-83) the predicted median as well as the significance level are specified.
The p-values given by this tool are determined using a normal approximation. This approximation is only valid if the sample size is at least 12.
Suppose you want to perform a Wilcoxon Signed Rank Test on the data given in Figure 8-82 to determine whether the sample comes from a population of mean 3.
- Enter A1:A19 (or Sheet1!$A$1:$A$19) in the “Input Range:” entry by typing this directly into the entry or clicking in the entry field and then selecting the range on the sheet.
- Select the “” option since the first row contains a label. (see Figure 8-82).
- On the “” tab of the dialog (see Figure 8-83) select the Wilcoxon Signed Rank Test.
- Specify an appropriate significance level Alpha, say 0.05.
- Select thepecify the median of the null hypothesis (3) in the “” entry.
- Specify the output options as described above.
- Press the OK button.
The output of this sign test is shown in Figure 8-85.
8.6. Two Sample Tests
8.6.1. Comparing Means of Two Populations
Gnumeric provides four similar tools to test whether the difference of two population means is equal to a hypothesized value. These four tools use the same dialog (see Figure 8-86).
Depending on the options settings, the appropriate test will be performed. The entries in the “Input”, “Test”, and “Output” frames are independent from the specific test.
Enter the first variable in the “Variable 1 Range” entry and the second variable in the “Variable 2 Range” entry.
Enter the hypothesized difference between the population means in the “Hypothesized Mean Difference” entry, which has a default of 0. Enter the significance level in the “Alpha” entry, which has a default of 5 %.
Specify the output options as described above. If the output is printed into a range, it should have at least three columns and ten rows.
There are up to three possible options that can be selected:
- “Paired” versus “Unpaired”
If the variables are dependent (or paired) select the “Paired” option.
- “Known” versus “Unknown”
For unpaired or independent variables, the population variances may be known or unknown. In the latter case they will be estimated using the sample variances. Select the “Known” option if you in fact know the population variances prior to collecting the sample.
- “Equal” versus “Unequal”
For paired variables with unknown population variances, we may either assume that the population variances are equal or not. If the population variances are assumed to be equal, Gnumeric will estimate the common variance by pooling the sample variances. Select the “Equal” option to assume that the population variances are equal.
8.6.1.1. t-Test: Paired Two Sample for Means Tool
For paired variables, when you click on “”, Gnumeric will test whether the mean of the difference between the paired variables is equal to the given hypothesized mean difference.
See Figure 8-88 for an example of a completed dialog and Figure 8-89 for the corresponding output.
8.6.1.2. t-Test: Two-Sample Assuming Equal Variances Tool
For unpaired variables with unknown but assumed equal population variances, when you click on “”, Gnumeric will test whether the mean of the difference between the paired variables is equal to the given hypothesized mean difference.
See Figure 8-91 for an example of a completed dialog and Figure 8-92 for the corresponding output.
8.6.1.3. t-Test: Two-Sample Assuming Unequal Variances Tool
For unpaired variables with unknown and assumed unequal population variances, when you click on “”, Gnumeric will test whether the mean of the difference between the paired variables is equal to the given hypothesized mean difference.
See Figure 8-94 for an example of a completed dialog and Figure 8-95 for the corresponding output.
8.6.1.4. z-Test: Two Samples for Means Tool
For unpaired variables with known population variances, enter those variances in the “Variable 1 Pop. Variance” and “Variable 2 Pop. Variance” entries. When you click on “”, Gnumeric will test whether the mean of the difference between the paired variables is equal to the given hypothesized mean difference.
See Figure 8-97 for an example of a completed dialog and Figure 8-98 for the corresponding output.
8.6.2. Comparing Medians of Two Populations
Gnumeric provides three non-parametric tests to test the null hypothesis that the two samples come from populations with the same median. Two tests, performed through the same tool, apply in the case of paired samples:
- Sign Test
- Wilcoxon Signed Rank Test
One test applies in the case of unpaired samples:
- Wilcoxon-Mann-Whitney Test
- 8.6.2.1. Sign Test
- 8.6.2.2. Wilcoxon Signed Rank Test
- 8.6.2.3. Wilcoxon-Mann-Whitney Test
8.6.2.1. Sign Test
This section describes the two sample (paired) sign test to test the null hypothesis that the two samples come from populations with the same median. The tool to perform a sign test to test the null hypothesis that the single sample comes from a population with a given median is in section Section 8.5.2.1 ― Sign Test.
This section needs to be written.
8.6.2.2. Wilcoxon Signed Rank Test
This section describes the two sample (paired) Wilcoxon signed rank test to test the null hypothesis that the two samples come from populations with the same median. The tool to perform a Wilcoxon signed rank test to test the null hypothesis that the single sample comes from a population with a given median is in section Section 8.5.2.2 ― Wilcoxon Signed Rank Test.
This section needs to be written.
8.6.3. F-Test: Two-Sample for Variances Tool
Use the F-Test tool to test whether two population variances are different against the null hypothesis that they are not.
Specify the variables in the “Variable 1 Range:” and “Variable 2 Range:” entries. The “Alpha:” entry contains the significance level which is by default 5%.
If the first field of each range contains labels, select the “” option. The names of the variables will be included in the output table.
The results are given in a table. This table contains the mean, variance, count of observations and the degree of freedom for both variables. The output table also includes the F-value, the one-tailed probability for the F-value, and the F Critical value for one-tailed test and the corresponding values for a two tailed test. The one-tailed probability for the F-value (“P(F≤f) one-tail” row) is the probability of making a Type I error in the one-tailed test. Similarly, the two-tailed probability for the F-value (“P two-tail” row) is the probability of making a Type I error in the two-tailed test. Since in the two-tailed F-Test both critical values are positive, the “F Critical two-tail” row contains two numbers.
If the output is directed into a specific output range, that range should contain at least three columns and eight rows.
Figure 8-100 shows some example data and Figure 8-101 the corresponding output.
8.7. Multiple Sample Tests
- 8.7.1. Analysis of Variance
- 8.7.2. Tests for a Contingency Table
8.7.1. Analysis of Variance
- 8.7.1.1. ANOVA: Single Factor Tool
- 8.7.1.2. ANOVA: Two-Factor Tool
8.7.1.1. ANOVA: Single Factor Tool
Use this tool to perform a single factor analysis of the variances of given variables. The variables are specified by the “Input Range:” entry. The given range can be grouped into the variables either by columns, by rows or by areas. The “Alpha:” entry specifies the significance level which is by default 5%.
If the first row or first column of the given range, or the first field of each area contains labels, select the “” option. The names of the variables will be included in the output table.
The results of this analysis of variance are presented in a standard ANOVA table. The “F critical” value is the largest value of F that is statistically significant using the given significance level (“Alpha”).
This tool also calculates the count, sum, average, and the variance of each variable.
See Figure 8-102 for an example of a completed dialog and Figure 8-103 for the corresponding output.
8.7.1.2. ANOVA: Two-Factor Tool
Gnumeric can perform two factor fixed effects ANOVAs with and without replication. The same dialog is used and the appropriate tool is selected depending on whether the number of rows per sample is 1 or larger than 1.
- 8.7.1.2.1. ANOVA: Two-Factor Without Replication Tool
- 8.7.1.2.2. ANOVA: Two-Factor With Replication Tool
8.7.1.2.1. ANOVA: Two-Factor Without Replication Tool
If the number of rows per sample is given as 1, Gnumeric performs a two factor fixed effects ANOVA without replication. Each column of the input range is interpreted as a level of the first factor while each row is interpreted as a level of the second factor.
The first row and column of the range may contain labels for these levels. In this case the “” option should be selected.
The “Alpha:” entry specifies the significance level which is by default 5%.
See Figure 8-104 for an example of a completed dialog and Figure 8-105 for the corresponding output.
8.7.1.2.2. ANOVA: Two-Factor With Replication Tool
If the number of rows per sample is larger than 1, Gnumeric performs a two factor fixed effects ANOVA with replication. Each column of the input range is interpreted as a level of the first factor while groups of rows (the number of rows in each group given by the “number of rows per sample” value) are interpreted as levels of the second factor.
The first row and column of the range may contain labels for these levels. In this case the “” option should be selected.
The “Alpha:” entry specifies the significance level which is by default 5%.
See Figure 8-106 for an example of a completed dialog and Figure 8-107 for the corresponding output.
Gnumeric will estimate missing values for each level combination as the mean of the existing values in that combination. The degrees of freedom are adjusted appropriately.
9. Graphics: Images, Widgets, and Drawings
This chapter explains how to add graphical elements to a Gnumeric worksheet, including images from external files, graphical user interface widgets which interact with worksheet data, and simple drawing elements.
- 9.1. Overview
- 9.2. Images
- 9.3. GUI Widgets
- 9.4. Drawing Elements
9.1. Overview
Gnumeric provides several types of graphical elements which can be added to a worksheet. The creation, manipulation and deletion of these elements all occur in similar ways. When these elements are part of a worksheet, they all "float" above the cell grid, possibly hiding data in the cells underneath.
Gnumeric currently displays four different types of graphical elements: data graphs, images, widgets, and drawings. Data graphs allow users to present worksheet data visually in charts containing several kinds of plots including pie plots, bar and column plots, and scatterplots. Images in many standard computer formats can be added to a worksheet. Graphical user interface widgets can also be added to a worksheet and connected to the values contained in worksheet cells. Drawings allow users to add simple graphical elements on top of a worksheet including lines, arrows and simple polygons.
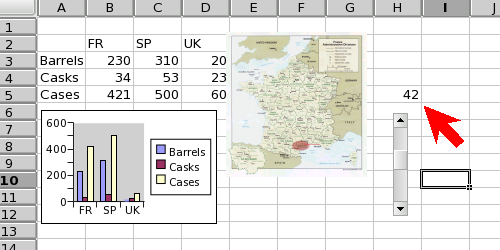
The four types of graphical elements which can be added to a worksheet: a data graph with a column plot, an image showing a map of France, a scrollbar which can be used to alter the value in cell "I6", and a red arrow drawing element.
The various graphical elements which can be added to a Gnumeric worksheet all behave in similar ways. The graphical elements all "float" above the cells in the cell grid and may obscure the contents of the cells behind, without affecting the contents of these hidden cells. All graphical elements are added in essentially the same way by selecting the element to add and then using the mouse, either with a simple click to place the element with a default size or with a click and drag to select the area of the worksheet to be covered by the element. These objects are moved or re-sized by clicking on the object with the primary mouse button and using the object body, border and "handles" (the small circles which appear at the corners and in the middle of each side) to manipulate the object. All of these objects will present a context menu through which to change the properties of the object, to save the object as an image, to change the stacking order (which graphical elements are in front of others), or to delete the object. Each of these operations will be summarized below and then explained in greater detail in the sections which follow.
- 9.1.1. Adding Graphical Elements
- 9.1.2. Selecting Graphical Elements
- 9.1.3. Moving and Resizing Graphical Elements
- 9.1.4. Invoking the Context Menu for Graphical Elements
- 9.1.5. Modifying Graphical Elements
- 9.1.6. Saving Graphical Elements as Images
- 9.1.7. Restacking Graphical Elements
- 9.1.8. Deleting Graphical Elements
9.1.1. Adding Graphical Elements
All graphical elements are added in similar ways which differ only in the original selection and configuration of the element. Data graphs are added using the Graph Guru, which is invoked either through the menu or with the toolbar button, to define the properties of the graph. Images are added using the menu menu entry, selecting the name of the file with the appropriate image and clicking on the button. Widgets and drawing elements are added by selecting the appropriate button on the object toolbar.
After any of these steps, the mouse cursor will change into a
thin cross-hair cursor,  ,
when the mouse pointer is placed over the cell grid area.
,
when the mouse pointer is placed over the cell grid area.
The graphical element can be placed in the workbook by moving the cursor onto the worksheet and clicking once with the primary mouse button. The graphical element will appear at its default size with the top right hand corner defined by the position of the mouse cursor.
Alternatively, the graphical element can both be placed on the worksheet and have its size determined which is done by click-dragging with the mouse. When the cursor has changed to the thin cross-hair, the graphical element can be inserted by moving the pointer over the worksheet to determine one of the corners of the resulting element, clicking and holding the primary mouse button, dragging the pointer to the opposite corner, and releasing the mouse button. The graphical element will then appear between the place where the primary mouse button was pressed and the place the button was released.
9.1.2. Selecting Graphical Elements
Selecting the graphical element requires placing the mouse pointer over the element and then clicking the primary mouse button. Gnumeric indicates the element is selected by drawing eight 'grab handles' around the element; these are small circles at the four corners and in the middle of the four edges of a rectangle surrounding the graphical element.

The graphical column plot has been selected as evidenced by the eight small circular 'grab handles' at the corners and in the middle of each edge.
The mouse pointer will also change shape when placed over a
selected element or over the element's 'grab handles'. When the
pointer is placed over a selected element, the mouse pointer
will change to the 'move' shape,  ;
when the pointer is placed over the element's 'grab handles' it
will change to one of the resizing mouse pointer shapes, which
are presented in Section 4.8 ― The Mouse Pointers used by Gnumeric.
;
when the pointer is placed over the element's 'grab handles' it
will change to one of the resizing mouse pointer shapes, which
are presented in Section 4.8 ― The Mouse Pointers used by Gnumeric.
Some elements, such as the widget scrollbars, may be difficult to select because they interact themselves with the primary mouse button. An alternative selection process, which involves first invoking the context menu and then dismissing it, can be used for these elements and will work with any graphical element. When the mouse pointer is anywhere over the graphical element, clicking with one of the secondary mouse buttons will cause the element to be selected and a context menu to appear. If the primary mouse button is then pressed while the pointer is anywhere over the desktop other than over the menu, the context menu will be dismissed but the element will stay selected.
9.1.3. Moving and Resizing Graphical Elements
Graphical elements can be moved from their original location on the worksheet or can be changed in size or shape. All of these operations first require selecting the graphical element with the primary mouse button and then using this mouse button and the mouse pointer to manipulate the element.
- 9.1.3.1. Moving elements with the mouse
- 9.1.3.2. Moving elements with the arrow keys
- 9.1.3.3. Resizing and reshaping elements
9.1.3.1. Moving elements with the mouse
Moving the graphical element can be performed by first selecting
the graphical element, then placing the mouse pointer over the
element which will change it to the 'move' mouse shape,
 ,
clicking and holding the primary mouse button and moving the
mouse pointer to a new location. As the mouse is moved with the
primary mouse button held down, the graphical element will move
along with the mouse cursor. When the mouse button is released,
the object will stay in its new location.
,
clicking and holding the primary mouse button and moving the
mouse pointer to a new location. As the mouse is moved with the
primary mouse button held down, the graphical element will move
along with the mouse cursor. When the mouse button is released,
the object will stay in its new location.
9.1.3.2. Moving elements with the arrow keys
Once they are selected, graphical elements can be moved with the arrow keys on the keyboard. The movement can be made in smaller increments if the Ctrl key is held simultaneously.
9.1.3.3. Resizing and reshaping elements
Changing the size or shape of the graphical element can be performed by selecting the graphical element, placing the mouse pointer over one of the 'grab handles' at the corners or edges of the rectangular box around the element, which will cause the mouse pointer to change shape to one of the resize pointers, clicking and holding with the primary mouse button, dragging the corner or edge to a new position, and releasing the mouse button. If one of the corner 'grab handles' is used, the graphical element can be altered into any new rectangular shape and size. If one of the edge handles is used, the element can only be reshaped perpendicular to the chosen edge.
9.1.4. Invoking the Context Menu for Graphical Elements
Many operations on graphical elements, including changing their internal properties, saving elements as images, modifying the stacking order of the elements, and deleting the elements, are performed through the context menu. The context menu appears when the mouse pointer is placed over the graphical element and one of the secondary mouse buttons is clicked. When the mouse pointer moves over a graphical element, it will change from the usual wide cross cursor to a right pointing arrow cursor. Clicking with the primary mouse button will select the graphical element but clicking with one of the other mouse buttons will open the context menu. The specific button that will trigger this menu depends on the specific hardware and configuration of the computer. By default it is usually the rightmost mouse button.
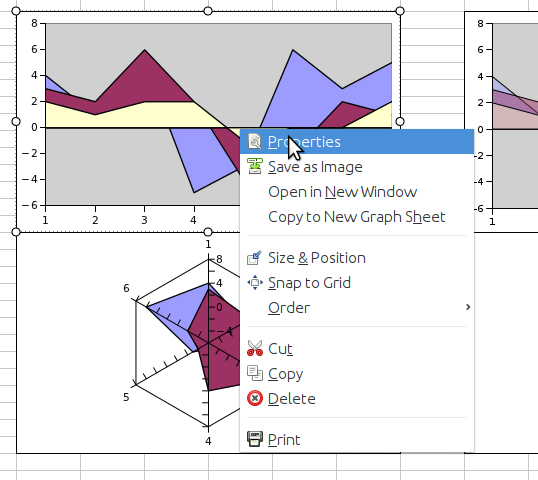
The context menu for graph elements is the most complete. It includes an entry to modify the internal properties of the graph, an entry to save the graph as an image, four entries to reorder the stacking of the graph in front or behind other graphs and one entry to delete the graph.
The context menu for graphical elements contains a sub-menu labelled which allows the user to change the presentation order for overlapping graphical objects.

The order submenu of the context menu for graph elements allows the user to change the stacking order for the various graphs on the worksheet. This will affect which objects are visible in front of other objects when several objects overlap.
9.1.5. Modifying Graphical Elements
Many of the graphical elements have internal properties which can be changed. This includes the contents of a particular graph, the association of a widget and the contents of a spreadsheet cell, or the characteristics of a drawing element. These properties can be altered using the menu item in the context menu which appears when the mouse pointer is placed over the graphical element and one of the secondary mouse buttons is clicked. After the context menu appears, clicking on this menu item will open up a dialog allowing the user to alter the properties of the element. Since these properties are specific to each element, these dialogs will be discussed in each of the sections below.
9.1.6. Saving Graphical Elements as Images
Some of the graphical elements, the data graphs and the image elements, provide an item in the context menu which allows the element to be saved to a file containing only an image of that element. Graphical plots can be saved in Scalable Vector Graphics (SVG), Portable Network Graphics (PNG) or JPEG formats. Images can be saved to their original format, or to PNG and JPEG formats.
Elements which can be saved as images can be output to a file using an entry in the element's context menu. First the context menu must be invoked by placing the mouse pointer over the graphical element and clicking with one of the secondary mouse buttons. Next the or the menu items must be selected by placing the mouse pointer over that item and clicking with the primary mouse pointer. This will open up the Save As dialog which will allow the user to name the file which will be created, select where the file will be created, select the file type to use for the image and then generate the file.
9.1.7. Restacking Graphical Elements
Graphical elements can overlap when they are placed over the cell grid area. Conceptually, each graphical element occupies one layer in a stack of all the elements. By default, elements which have been created more recently will overlap in front of elements which were created earlier.
The order of each element in the stack can be changed using the four menu items in the context menu. The will bring the selected element in front of all the other objects. The menu item will bring the selected element forward one layer. Conversely, the menu item will move the selected element one layer towards the back, and the menu item will palace the selected element at the very back of the stack of elements. Jointly, these menu items allow the user to specify exactly which order in which the graphical elements should appear.
The stacking of graphical elements in Gnumeric is currently not working correctly. Widget elements are always placed above the other elements and do not honor the same ordering scheme as the rest of the elements. A large amount of work will be required to fix this and a decision has been made to ignore this problem until the developers have the time to fix this problem correctly.
9.1.8. Deleting Graphical Elements
All of the graphical elements in Gnumeric can be deleted using the context menu. Deleting a graphical element will never alter the data contents of the cells in the workbooks.
Deleting a graphical element requires using the context menu. First the mouse pointer must be placed over the graphical element. Next, the context menu must be invoked by clicking with one of the secondary mouse buttons. Finally, the menu item must be selected by placing the mouse pointer over this menu item and clicking with the primary mouse button. When this menu item is selected, the graphical element will disappear from the worksheet and will not be saved as part of the spreadsheet file the next time the file is saved.
9.2. Images
Images can be added, as floating graphical elements, to Gnumeric worksheets. These images will be saved as part of the file and therefore can be sent to others embedded within the spreadsheet file.
Images in several file formats can be added, but the specific list depends on the particular installation of the underlying software library, gdk-pixbuf. By default, the ANI, BMP, GIF, ICO, JPEG, PCX, PNG, PNM/PBM/PGM/PPM family, Sun raster (RAS), Targa (TGA), TIFF, WBMP, XBM, XPM image formats are supported, but extensions to the library can also support other formats such as the WMF Windows Metafile and SVG Scalable Vector Graphics formats.
A complete listing of the file formats supported by the local version of gdk-pixbuf can be generated with the
gdk-pixbuf-query-loaders
- 9.2.1. Inserting Images
- 9.2.2. Saving Images to New Files
- 9.2.3. Deleting Images
9.2.1. Inserting Images
Inserting an image is performed like inserting any other graphical element using the menu entry to start the process, then selecting the file, and finally using the mouse to place the image above the worksheet.
-
Select the menu item in the menu
Inserting an image starts by selecting, in the menu, the menu item using the mouse cursor and the primary mouse button. This will open a dialog in which the user can select the file which contains the desired image.
-
Select the file containing the image
In the dialog which appears the user must select the file which contains the desired image. The dialog will be specific to the particular operating system platform but should provide a way to navigate the filesystem to pick the folder that contains the file and have a way to select the file or type its name. When these choices have been made, the dialog can be dismissed by double clicking on the file or by clicking on the button. This will dismiss the dialog and expose the worksheet, with the mouse pointer now converted to a thin cross-hair.
-
Place the image on the worksheet with the mouse pointer
The image, which will float like other graphical elements above the worksheet, must be placed on the worksheet. The image can be placed with its default size by moving the thin cross-hair pointer above the worksheet and clicking with the primary mouse button. Alternatively, the image can be placed and sized by selecting two of the resulting corners. This is done by moving the thin cross-hair pointer over the worksheet, determining one corner by clicking and holding the primary mouse button, dragging the pointer to the opposite corner, and releasing the mouse button. The image will then appear between the place where the primary mouse button was pressed and the place the button was released.
9.2.2. Saving Images to New Files
Images in a Gnumeric worksheet can be saved to a new, separate file. The image can be saved either in its original format or in PNG or JPEG formats. The ability to save images to a new file is especially useful when a spreadsheet file has been transferred to a computer that does not have a copy of the original image.
Images above a worksheet can be saved by accessing the context menu, selecting the many entry and navigating the file saving dialog which appears.
-
Open the context menu
The context menu is opened by placing the mouse cursor over the image and clicking one of the secondary mouse buttons.
-
Select the menu item
Once the context menu appears, the mouse cursor can be moved over the menu. As the cursor passes over each menu item, that item will be highlighted. When the menu item is highlighted, clicking with the primary mouse button will select that entry, causing the context menu to disappear and the Save As dialog to appear.
-
Select the file name and location
The Save As dialog which opens will depend on the platform that the user is using but should be standard for that platform. The dialog should allow a user to define a name for the file, to select the folder (directory) in which a file will be saved, and to select the format for the saved file. When all these selections have been made, the can be pressed which will dismiss the dialog and save the file.
9.2.3. Deleting Images
An image element, floating above a worksheet, can be deleted from the worksheet and from the Gnumeric file using the context menu. The procedure for deleting all graphical elements is the same; this procedure is explained in Section 9.1.8 ― Deleting Graphical Elements.
9.3. GUI Widgets
A Gnumeric worksheet can graphical user interface (GUI) elements, commonly called 'widgets', which can be tied to the data contents of worksheet cells. For example, users can add a slider widget which, when the position of the slider moves, alters the numeric value in a worksheet cell.
The current implementation of these widgets is incomplete. Some of the obvious configuration settings for these widgets do not exist and much of the functionality that these widgets should exhibit has not been implemented. Future versions of Gnumeric will complete these widgets and make them functional.
Widgets currently stay above all the other graphical elements because they use a different system to calculate their positions than the other graphical elements do. This will also be fixed in future updates.
Each of these elements can be added by selecting the appropriate icon on the object toolbar and using the thin cross-hair mouse pointer to place the element on the worksheet by clicking or by click-dragging with the primary mouse button. This process is explained in greater detail in Section 9.1.1 ― Adding Graphical Elements.
Each of these elements can be configured using the context menu and its menu item, as explained in Section 9.1.5 ― Modifying Graphical Elements.
Each of these elements can be moved and resized on the worksheet, as explained in Section 9.1.3 ― Moving and Resizing Graphical Elements.
The stacking order, from the front to the back, which determines which widgets obscure each other, can be changed using the entries in the context menu, as explained in Section 9.1.7 ― Restacking Graphical Elements. However, as explained in the note above, the widgets do not currently stack under the other graphical elements.
Each of these elements can be deleted using the context menu and its menu item, as explained in Section 9.1.8 ― Deleting Graphical Elements.
- 9.3.1. Labels.
- 9.3.2. Frames.
- 9.3.3. Checkboxes.
- 9.3.4. Scrollbars.
- 9.3.5. Spinbuttons.
- 9.3.6. Sliders.
- 9.3.7. Lists.
- 9.3.8. Combination Boxes.
9.3.1. Labels.
Labels are intended to be small text elements which can be added to the worksheet. Since it is currently not possible to edit the text field, these widgets are not currently usable. The properties of the border and background of the widget can be changed but, because the word "Label" is always present, the rectangle drawing element, presented in Section 9.4.3 ― Drawing Rectangles. will be more useful.
9.3.1.1. Configuring the properties of the label
The properties of the label can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the label and one of the secondary mouse buttons is pressed.
The label outline color and width, as well as the background, "fill", color can be changed.
The color of the label outline can be altered by moving the mouse pointer over the button with the icon of a small, black, downward pointing arrow and then clicking with the primary mouse button. This will open up a panel with a number of standard colors presented as small squares. Any of these colors can be selected by moving the mouse pointer over the desired color and pressing once with the primary mouse button. Alternatively, a custom color can be chosen by clicking on the button at the bottom of the panel. This will open up the color chooser dialog. In this dialog colors can be defined using the numeric boxes or can be selected using the color triangle. The color can be selected by Clicking on the outer circle while the darkness or lightness can be selected by clicking inside the triangle. Once the desired color has been configured, this color can be used for the label outline by clicking on the button.
The border width can be changed either by typing a new number into the text box or by using the up and down arrows to increment or decrement the width number.
The color of the background fill can be changed in the same way as the color of the outline border, which was explained above.
9.3.2. Frames.
Frames are intended to be transparent boxes with a title that can be placed around part of the worksheet to highlight that area. Because the format of the border of these widgets cannot be altered, they are less visible than they could be. A similar frame, without the title, can be made with the rectangle drawing element, which is presented in Section 9.4.3 ― Drawing Rectangles..
9.3.2.1. Configuring the properties of the checkbox
The properties of the frame can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the frame and one of the secondary mouse buttons is pressed.
Currently, only the word that appears in the frame can be altered.
The word displayed in the frame can be altered by typing new text in the textbox next to the word "Label".
9.3.3. Checkboxes.
Checkboxes are widgets which allow a user to visually see the state of an entity, whether it is checked or not, and tie this state to the truth value of a Boolean cell, "TRUE" if the checkbox is checked and "FALSE" the checkbox is not. The check box can be used to alter the value of a cell, which will alter any other cells whose values are computed based on the dependent cell. This provides a simple way to alter a whole series of computations.
9.3.3.1. Configuring the properties of the checkbox
The properties of the checkbox can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the checkbox and one of the secondary mouse buttons is pressed.
Checkboxes have two properties which can be configured: the worksheet cell whose value will be altered by clicking in the checkbox and the text displayed on the checkbox.
The "Link to:" field allows the user to select a cell that will be changed in response to changes in the state of the widget. A user can type the name of a cell in the text box or may click in the text box to activate it and then click on the worksheet to select the desired cell and Gnumeric will automatically add a reference to the cell.
The "Label" field accepts a text value which will appear next to the checkbox. This text can indicate what the checkbox field alters, for instance in Figure 9-10 the checkbox could be used to alter a series of calculations, between including interest or excluding it, from the computation.
9.3.4. Scrollbars.
Scrollbars are widgets that allow the changing of a numeric value by click-dragging with the mouse.
The scrollbar widget can be used in three ways: by dragging the 'thumb', by clicking on the arrows, or by clicking in the 'channel'. The 'thumb' is the small rectangular element between the two arrow buttons. The 'thumb' can be dragged by placing the mouse pointer over the thumb, clicking and holding with the primary mouse button and then dragging the mouse pointer up or down. Clicking on the arrow buttons will scroll the thumb in the direction of the arrow. The 'channel' is the area between the arrows that is not the 'thumb'. A mouse click with the primary mouse button when the mouse pointer is over the 'channel' will cause the scrollbar to move a 'page'. The motion of the 'thumb' will cause a numeric value to change based on the configuration of the widget, as is explained below.
9.3.4.1. Configuring the properties of the scrollbar
The properties of the scrollbar can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the scrollbar and one of the secondary mouse buttons is pressed.
Scrollbars have five properties which can be configured: the worksheet cell whose value will be altered by movement of the scrollbar 'thumb', the minimum value when the thumb is at the top of its channel, the maximum value reached when the thumb is at the bottom of its channel, the smallest increment of change which is the change caused by clicking on the arrows, and the page increment which is the change which occurs when the channel is clicked.
The "Link to:" field allows the user to select a cell that will be changed in response to changes in the state of the widget. A user can type the name of a cell in the text box or may click in the text box to activate it and then click on the worksheet to select the desired cell and Gnumeric will automatically add a reference to the cell.
The other properties can be changed either by typing a new number into the text box or by using the up and down arrows to increment or decrement the width number.
9.3.5. Spinbuttons.
Spinbuttons, like sliders, are widgets that allow a user to change the numeric value in the cell by interacting with a widget. The value of spinbuttons can be changed either by typing a new number into the text box or by clicking on the arrow buttons. If the buttons are clicked and held, the numeric value will spin, incrementing or decrementing depending on the arrow being held.
9.3.5.1. Configuring the properties of the spinbutton
The properties of the spinbutton can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the spinbutton and one of the secondary mouse buttons is pressed.
Spinbuttons have five properties which can be configured: the worksheet cell whose value will be altered by the spinbutton, the minimum value when the thumb is at the top of its channel, the maximum value reached when the thumb is at the bottom of its channel, the smallest increment of change which is the change caused by clicking on the arrows, and the page increment which is the change which occurs when the channel is clicked.
The "Link to:" field allows the user to select a cell that will be changed in response to changes in the state of the widget. A user can type the name of a cell in the text box or may click in the text box to activate it and then click on the worksheet to select the desired cell and Gnumeric will automatically add a reference to the cell.
The other properties can be changed either by typing a new number into the text box or by using the up and down arrows to increment or decrement the width number.
9.3.6. Sliders.
Sliders, like scrollbars and spinbuttons, allow a cell value to be changed based on user interaction with a widget on the screen.
The slider widget can be used in two ways: by dragging the 'thumb' or by clicking in the 'channel'. The 'thumb' is the small rectangular element between the two arrow buttons. The 'thumb' can be dragged by placing the mouse pointer over the thumb, clicking and holding with the primary mouse button and then dragging the mouse pointer up or down. The 'channel' is the area between the arrows that is not the 'thumb'. A mouse click with the primary mouse button when the mouse pointer is over the 'channel' will cause the scrollbar to move a 'page'. The motion of the 'thumb' will cause a numeric value to change based on the configuration of the widget, as is explained below.
9.3.6.1. Configuring the properties of the slider
The properties of the slider can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the slider and one of the secondary mouse buttons is pressed.
Sliders have five properties which can be configured: the worksheet cell whose value will be altered by movement of the scrollbar 'thumb', the minimum value when the thumb is at the top of its channel, the maximum value reached when the thumb is at the bottom of its channel, the smallest increment of change, and the page increment which is the change which occurs when the channel is clicked.
The "Link to:" field allows the user to select a cell that will be changed in response to changes in the state of the widget. A user can type the name of a cell in the text box or may click in the text box to activate it and then click on the worksheet to select the desired cell and Gnumeric will automatically add a reference to the cell.
The other properties can be changed either by typing a new number into the text box or by using the up and down arrows to increment or decrement the width number.
9.4. Drawing Elements
A Gnumeric worksheet can contain graphical elements which are simple drawing shapes.
This implementation of the drawing objects is temporary and will eventually be replaced by a more complete implementation including more types of drawing objects and based on scalable vector graphics (SVG) format graphical elements.
Each of these elements can be added by selecting the appropriate icon on the object toolbar and using the thin cross-hair mouse pointer to place the element on the worksheet by clicking or by click-dragging with the primary mouse button. This process is explained in greater detail in Section 9.1.1 ― Adding Graphical Elements.
Each of these elements can be configured using the context menu and its menu item, as explained in Section 9.1.5 ― Modifying Graphical Elements.
Each of these elements can be moved and resized on the worksheet, as explained in Section 9.1.3 ― Moving and Resizing Graphical Elements.
The stacking order, from the front to the back, which determines which widgets obscure each other, can be changed using the entries in the context menu, as explained in Section 9.1.7 ― Restacking Graphical Elements. However, as explained in the note above, the widgets do not currently stack under the other graphical elements.
Each of these elements can be deleted using the context menu and its menu item, as explained in Section 9.1.8 ― Deleting Graphical Elements.
- 9.4.1. Drawing Lines.
- 9.4.2. Drawing Arrows.
- 9.4.3. Drawing Rectangles.
- 9.4.4. Drawing Ovals.
9.4.1. Drawing Lines.
Lines are simple drawing elements which can be added to a worksheet. Figure 9-20 shows a wide orange line element placed above the worksheet grid.
9.4.1.1. Configuring the properties of the line
The properties of the line can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the line and one of the secondary mouse buttons is pressed.
Lines have two properties, the color used for the line and the width of the line.
The color of the line can be altered by moving the mouse pointer over the button with the icon of a small, black, downward pointing arrow and then clicking with the primary mouse button. This will open up a panel with a number of standard colors presented as small squares. Any of these colors can be selected by moving the mouse pointer over the desired color and pressing once with the primary mouse button. Alternatively, a custom color can be chosen by clicking on the button at the bottom of the panel. This will open up the color chooser dialog. In this dialog colors can be defined using the numeric boxes or can be selected using the color triangle. The color can be selected by Clicking on the outer circle while the darkness or lightness can be selected by clicking inside the triangle. Once the desired color has been configured, this color can be used for the label outline by clicking on the button.
The line width can be changed either by typing a new number into the text box or by using the up and down arrows to increment or decrement the width number.
9.4.2. Drawing Arrows.
Arrows are elements that can be used to point to values in a worksheet. Figure 9-22 shows a purple arrow floating over a worksheet
9.4.2.1. Configuring the properties of the arrow
The properties of the arrow can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the arrow and one of the secondary mouse buttons is pressed.
Arrows have five properties, the arrow color, the width of the line stem of the arrow, and tree dimensions for the arrow point which will be explained below.
The dimensions of related to the arrow are presented in Figure 9-24.
The 'Arrow Tip' is the distance from the point of the arrow to the base of the arrowhead where the shaft begins. The 'Arrow Length' is the distance from the arrow point to either of the outer side points of the arrow head, projected along the shaft of the arrow. The 'Arrow Width' is the distance between the two outer side points of the arrow head.
9.4.3. Drawing Rectangles.
Rectangles are areal drawing elements. Figure 9-25 shows a yellow rectangle with a blue border.
Rectangles have three properties which can be configured, the color and width of the border and the color of the interior of the rectangle.
9.4.3.1. Configuring the properties of the rectangle
The properties of the rectangle can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the rectangle and one of the secondary mouse buttons is pressed.
The color of the outline border can be configured by selecting a new color from the color picker as was explained in Section 9.4.1 ― Drawing Lines. for the line drawing element. The width of the border can be configured by typing a new dimension in the text box or by clicking on the increment arrows, up to increase the width and down to decrease the width. The color of the interior of the rectangle, the 'fill' color, can be configured in the same way as the color of the outline border.
9.4.4. Drawing Ovals.
Ovals are areal drawing elements. Figure 9-27 shows a red oval with a transparent background, which is a useful way to circle important ranges in a workbook.
Ovals, like rectangles, can be configured in the color and width of the outline border, and the color of the fill.
9.4.4.1. Configuring the properties of the oval
The properties of the oval can be altered with the menu item in the context menu which appears when the mouse cursor is placed over the oval and one of the secondary mouse buttons is pressed.
The configuration of these properties is the same as the configuration of the rectangle properties explained above.
10. Graphs
Gnumeric includes a powerful mechanism to create graphical charts which present visually the data contained in a worksheet.
The first section of this chapter starts with an overview of graph creation, discusses terminology, and presents graph components and their organization. The next section explains the "Chart Guru" which is the tool used to configure graphs. The subsequent section presents the different types of plots which can be included in a graph and the final section explains how data can be pre-selected to speed up the process of graph creation.
Charts are exceedingly effective communication devices. Unfortunately, this means that one cannot determine, simply based on the data to be plotted, what type of plot will be the most effective. Instead users must familiarize themselves with the various types of plots which are available and decide for themselves which plot type is the most effective to communicate an idea. Section 10.1 ― Overview of Graphs contains a detailed explanation of the plot types available in Gnumeric.
This chapter explains how to add graphs to plot worksheet data.
- 10.1. Overview of Graphs
- 10.2. The Graph Guru
- 10.3. Plot Types
- 10.4. Configuring Graph Element Properties
- 10.5. Pre-Selecting Data
10.1. Overview of Graphs
This overview will start with a brief summary of the process involved in creating a graph, then will discuss the terminology used in this document, will present the components of a graph, and present the hierarchy of the components used in to configure the graphs.
- 10.1.1. The Graph Creation Process
- 10.1.2. On Terminology
- 10.1.3. The Components of Graphs
- 10.1.4. The Graph Component Hierarchy
10.1.1. The Graph Creation Process
The process of graph creation involves several steps each of which requires the user to understand clearly what they intend to do. This outline is presented to help users understand the subsequent discussion in this document.
-
Data entry.
Before a graph can be created, the data must be entered into a workbook.
-
(Optional) Data pre-selection.
As explained in Section 10.5 ― Pre-Selecting Data, it is possible to pre-select the data and have Gnumeric correctly assign the cell contents into series names, category labels and data values. This process can only be understood once the rest of the graph creation process has been mastered so the discussion of pre-selecting data is left until the end of this section.
-
Opening the graph guru
The Graph Guru can be opened in two ways. It can be opened by clicking on the button,
 , which is on the standard toolbar
immediately to the left of the zoom box. Alternatively the
Graph Guru can be opened by using,
in the menu, the
menu item.
, which is on the standard toolbar
immediately to the left of the zoom box. Alternatively the
Graph Guru can be opened by using,
in the menu, the
menu item.
-
Configuring the graph
The Graph Guru provides the user with a large number of options to configure the graph, its charts and the plots. The first panel provides a way to select the plot type, sub-type and, for some types, a style. The second panel allows the user to configure each element of the graph. When the configuration is complete, the guru is dismissed by clicking the button. This step will be explained in detail in Section 10.2.2 ― Navigating the graph guru, below.
-
Inserting the graph
Finally, the graph is inserted into the worksheet like any other graphical element, as was explained in Section 9.1.1 ― Adding Graphical Elements.
10.1.2. On Terminology
The terminology used for describing the components of data graphs is confusing because graphs use many components and the words are applied arbitrarily to each component. For example, the words "graph", "chart", and "plot" could be used interchangeably but in Gnumeric these words are used as explained below.
The term 'graph' will be used, in this documentation, to refer to the entire graphical element placed on the worksheet. A graph has an outline and a background, may have one or more titles, and will have at least one 'chart'.
The term 'chart' will be used to denote an intermediate level element which has an outline and a background, may have one or more titles, may have a legend and will have at least one 'plot'. To support the plot, the chart may have a 'grid' area behind the plotted data, and have one or more axes.
Each 'plot' will be defined to be of a particular type when it is created. Plots will have one or more 'series' of data values which will define the magnitude of the values of to be plotted and may define a number of other related values including errors in the x and y directions.
This terminology can be used to describe in detail the components of a graph in Gnumeric. Figure 10-1 presents the components of a graph.
10.1.3. The Components of Graphs
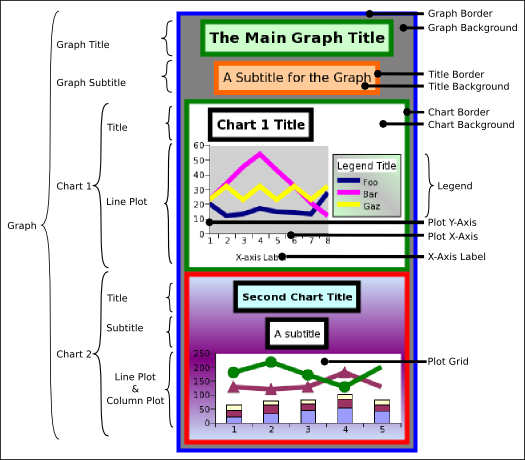
This screenshot presents several of the major components of Gnumeric graphs. These components will be presented next in their containment hierarchy. The hierarchy is used in the Graph Guru to organize the components so a user can change all the preferences.
10.1.4. The Graph Component Hierarchy
The components that make up a graph in Gnumeric are arranged in a hierarchy with all the configurable options of the graph assigned as properties to one of the components in the hierarchy.

The hierarchy of graph component elements and the associated properties. In this case, the element 'X-Axis2' is selected.
In Gnumeric, Graphs are the top level element containing all the other components. Graphs have two properties related to the style of the background rectangular panel, its fill and its outline. Graphs can hold one or more titles and one or more charts.
Titles have the same properties related to their background rectangular panel, the fill and outline, have properties related to the text, the font type, style, and size, and have the text data that will be the title itself.
Charts have the same properties related to the background rectangular panel and can contain a number of other components including their own titles, a legend, plot accessories and plots.
Legends have the same properties related to their background rectangular panel and also have the properties related to the font in which the name of each series will be added to the legend, the font type, style, and size.
Certain plot types require accessory components such as the elements related to the creation of a Cartesian coordinate system. Charts which include one or more plots of this kind will have a Grid and may have X (horizontal) and Y (vertical) axes.
Grids are the background of Cartesian plots and have the properties determining the fill of this area and the line pattern displayed behind the plotted series.
Axes have properties related to the outer bounds of the axis, the style of the line drawn for the axis, the font style of the markers along the axis, detail properties of the tics and other markers on the axis, and the number format of the axis markers.
Axis labels share the same properties related to the style of their background rectangular panel, including the fill and outline properties, have properties related to the style of the font used for the text, including the font type, style and size, and the data contents of the text used to label the axis.
The properties of each type of plot, and of the data series they contain, vary depending on the actual type of the plot. For instance, the values of a data series which are plotted as a pie plot will not have any associated error values, whereas values plotted as columns could be associated to Y-error values and values plotted as an XY scatterplot could be associated with error values in both the X and the Y direction. Obviously, these different plot types will require different options. The options associated with each specific plot type will be discussed below, in Section 10.4 ― Configuring Graph Element Properties.
10.2. The Graph Guru
All graphs in Gnumeric are created using the Graph Guru which is a complex dialog that allows for detailed customization of each graph.
- 10.2.1. The components of the Graph Guru
- 10.2.2. Navigating the graph guru
10.2.1. The components of the Graph Guru
The Graph Guru consists of two panels which appear sequentially. The first panel allows the user to select the type of the plot, and possibly a sub-type and a style. The second panel provides a way to configure the style formats of each component of the final graph. Figure 10-3 shows the different areas of the two panels of the Graph Guru.
The different parts of each panel of the Graph Guru have been shaded with boxes of different colors and labeled with a letter in Figure 10-3. The purpose of each of these sections will be explained below:
- - The Plot Type Selection Area
-
This area lists the different types of plots which can be contained within the graph. The desired plot type can be selected simply by placing the mouse cursor over the desired type and clicking with the primary mouse button. The blue highlight indicates the currently selected type.
- - The Preview Area.
-
This area shows a preview of the currently selected plot type/sub type combination using the default settings for this type of plot.
- - The Plot Subtype Area.
-
This area presents a number of icons which change depending on the plot type that has been selected. Certain icons represent plot sub-types, for example, distinguishing plots with columns that are side by side from plots with stacked columns. Other icons represent different plot styles, for example distinguishing line plots in which each data point is labeled with a graphical symbol from line plots where data points do not have any symbol. The highlight box around one icon indicates which icon is currently chosen.
Hovering the mouse pointer over one of these icons causes a description of the plot type to be shown next to the icon.
- - The First Panel Navigation Buttons
-
These buttons enable the user to navigate through the Graph Guru.
- The Button
-
The button should cause this section of the manual to open.
- The Button
-
The button will dismiss the Graph Guru and return the user to the Gnumeric worksheet.
- The Button
-
The button will dismiss the first panel of the Graph Guru and open up the second panel.
- The Button
-
The button will dismiss the Graph Guru and allow users to insert the graph, as it is currently defined, into the worksheet. The resulting graph may not include any plots or data but it can be modified subsequently using the context menu's menu entry.
- - The hierarchy tree of graph components
-
This area allows the user to navigate the hierarchy of graph components. The components are arranged in a tree with nodes indicated by arrowheads. Components can be selected by clicking on the component name with the mouse pointer and nodes can be expanded or collapsed by clicking on the arrowheads. The selection of different components in this area will cause different property options to be displayed in area since each component in the hierarchy has its own specific properties.
Immediately below the hierarchy are buttons that allow a user to modify the hierarchy of components by adding components with the button or by removing components with the button. The allows the user to change the stacking order of charts, moving them up or down, or of data series, moving them toward the front or back.
- - The preview area
-
This area shows a preview of the graph as it will look if the user clicks on the or at the bottom of the panel, in area .
- - The component properties selection area.
-
This area allows the user to change the graph by modifying the properties of the component that is selected (highlighted in blue) in area . For components which have multiple properties these may be grouped into related sets and placed on different tabs. By clicking on the tabs at the upper left, a user can access the properties in each set.
- - The second panel navigation buttons
-
If the guru is opened to create a new graph the buttons in this are act in the same way as the buttons in the first panel, in area except that the is now a and takes the user back to the first panel.
If the guru is opened to modify an existing graph the following buttons are shown (as in the screenshot Figure 10-3).
- The Button
-
The button should cause this section of the manual to open.
- The Button
-
The button will dismiss the Graph Guru and return the user to the Gnumeric worksheet, leaving the graph unchanged.
- The Button
-
The button will dismiss the Graph Guru and apply the changes to the current graph.
- - The panel rearrangement handles
-
These triple dots in various places of the two panels of the graph guru indicate that the mouse can be used to change the size of the different areas. These handles can be used by placing the mouse pointer above a handle, clicking and holding with the primary mouse button, then dragging the handle to a new position, and then releasing the mouse button.
10.2.2. Navigating the graph guru
Graphs in Gnumeric are created using the Graph Guru. The process involved in using this 'guru' essentially follows the alphabetical labels presented in Figure 10-3.
-
Data Pre-selection
Advanced users generally start by pre-selecting at least some of the data they will use in their plots. However, this step requires a complete understanding graphs and this step is not described here. Section 10.5 ― Pre-Selecting Data will explain data preselection once the rest of the graphing process has been explained.
-
Launching the Graph Guru
The Graph guru can be started in two ways. One way to start the Graph Guru is to click, with the primary mouse button, on the toolbar graph button,
 . Another way is to select, from the
menu, the
menu item. Both
approaches will launch the Graph Guru.
. Another way is to select, from the
menu, the
menu item. Both
approaches will launch the Graph Guru.
-
Selecting the plot type, sub-type, and style.
The Graph guru opens to the first of two panels. The areas of this panel are shown in the left hand side of Figure 10-3. This panel enables the user to select the type of the first plot in the chart, and its sub-type and style. To make a graph with multiple plots, a user should start by selecting the first plot; subsequent plots can be added later.
-
Picking the plot type
The first area, area , provides a list of the plot types. The user can pick one of the types by placing the mouse pointer on top of that appropriate entry in the list and clicking the primary mouse button. The blue highlight indicates which plot type has been chosen. The characteristics of the different plot types are explained extensively in Section 10.3 ― Plot Types.
-
Picking the plot sub-type and style
The second area of the first panel of the Graph Guru, labeled in Figure 10-3, presents one or more icons. The icons presented in this area will change depending on what plot type is highlighted in area . The icons provide a way to select a sub-type of plot, for example, the icons for the column plot type provide the choice between plotting columns of each data series side-by-side or plotting these columns stacked upon each other. These icons may also provide a way to quickly select different styles for the plot type, for example the icons for the line type provide a choice between plotting a simple line or placing markers at the points along the line. The sub-type cannot be changed in the next panel of the Graph Guru without deleting the plot and creating a new one. However, the style choices can be altered in the next panel. The meaning of each of these icons is explained in Section 10.3 ― Plot Types below grouped by plot type. If data has been pre-selected, clicking on the will present a preview of the plot type in area .
-
Moving to the next panel
Once a plot type has been chosen in area and an icon selected in area , the first panel has been completed. Clicking on the button will dismiss the first panel of the Graph Guru and bring up the second panel.
-
-
Configuring the plot
The second panel of the Graph Guru enables users to configure the plot. This includes determining the values which will actually be plotted, adding titles to various components, labels to the data series, names to data categories, and changing the appearance of the different components.
The simplest way both to learn the hierarchy of components in Gnumeric graphs and to understand the properties which can be changed for each component is to work sequentially through all of the components while both noting the components which can be added, listed in the drop down menu when the button is pressed, and observing the properties of the component which can be altered, shown in the lower part of the panel, the area labeled in Figure 10-3. Each component in the hierarchy can be selected in turn using the complete tree of all the components presented in the top leftmost area, labeled . Components can be selected by placing the mouse pointer over their name in this tree and then clicking with the primary mouse button. The currently selected component is indicated by the blue highlight on that line. Changing the selected component will also change the properties listed in area . Tree nodes, indicated by arrowheads in front of the name of a component, can be expanded or collapsed with alternative mouse clicks.
The second panel of the Graph Guru only allows two types of actions to be performed: the hierarchy of component elements can be modified or the properties of an element can be altered.
Once the plot is sufficiently configured, it can be placed on the worksheet to assess its appearance. The user can return to this panel of the Graph Guru using the context menu on the graph. The Graph Guru is dismissed by clicking on the button.-
The component elements of the graph can be changed using the buttons in area . Elements can be added, deleted or re-ordered.
- Adding component elements
-
An element can be added by selecting the parent element in the hierarchy presented in area and then clicking and holding the button. This action will reveal a drop down list including all the possible elements that can be added. By moving the mouse pointer onto the drop down list and releasing the mouse button while the pointer is over an element, that element will be added. To add a plot to a chart, it is necessary to navigate into the sub-menu to select the plot type and then into that sub-menu to select a plot sub-type or style in a process that mimics the process of selecting a plot discussed above.
- Deleting component elements
-
An element can be deleted by selecting the element in the hierarchy presented in area , and then clicking the button below the hierarchy.
- Re-ordering component elements
-
The order of some of the elements can be interchanged using the button below the element hierarchy. For example, if an element has two titles, the order of the titles could be swapped. Similarly the vertical order of charts can be interchanged. The effect on plots and series is different. For those elements, the order button changes the stacking order in the front to back dimension. For example, if a chart has a bar plot and a line plot, the order button will change which of the two plots is visible in front of the other.
-
The bottom area of the second panel, area in Figure 10-3, allows the user to configure the properties of each element in the hierarchy. When there are many properties, they will be grouped into similar sets and placed on different tabs. The detailed explanation of how to configure each property of each element will be explained in Section 10.4 ― Configuring Graph Element Properties below.
-
Place the graph
After exiting the Graph Guru, the user must place the graph on a worksheet. Immediately after exiting the Graph Guru, the mouse pointer will have changed to the thin cross-hair cursor. The user can place the graph by moving the pointer over the worksheet and clicking once with the primary mouse button. Alternatively, the user can place and size the graph by determining two of the corners of the graph. This is done by moving the pointer onto the worksheet to the first corner, clicking and holding the primary mouse button, dragging the mouse pointer to the opposite corner and releasing the mouse button.
-
Modifying an existing graph
A graph which has already been created can be modified by clicking on the graph with one of the secondary mouse buttons in order to invoke the context menu and then selecting the menu entry. This will cause the second panel of the Graph Guru to appear which will enable the user to make any desired modifications. The use of the context menu was discussed in Section 9.1.4 ― Invoking the Context Menu for Graphical Elements.
-
Deleting a graph
A graph which has been made can be deleted by invoking the context menu and selecting the menu item.
10.3. Plot Types
Gnumeric graphs can include any of the plot types presented below. The section for each type explains the overall concept of the plot, gives an example, explains the data required for the plot type, and explains the icons in the Graph Guru which allow setting the plot sub-type and style.
- 10.3.1. Area Plots
- 10.3.2. Bar Plots
- 10.3.3. Bubble Plots
- 10.3.4. Colored XY Plots
- 10.3.5. Column Plots
- 10.3.6. Contour Plots
- 10.3.7. DropBar Plots
- 10.3.8. Line Plots
- 10.3.9. Min-Max Plots
- 10.3.10. Pie Plots
- 10.3.11. Polar Plots
- 10.3.12. Radar Plots
- 10.3.13. Ring Plots
- 10.3.14. Statistics Plots
- 10.3.15. Surface Plots
- 10.3.16. XY Scatterplots
10.3.1. Area Plots
Area plots present the numeric values of categorical data with the data values of each series connected by a line and the area below the line shaded. This type is directly analogous to the line plot type. Sequential data values are considered to belong to different categories and are plotted along the horizontal axis at equally spaced intervals. The data values from different series are assigned to these categories based on the position of the value in the series, for example, the second data value taken from each series all share one category. The data values are plotted along the vertical (Y) axis according to their numeric value and the particular sub-type chosen for the area plot.
Area plot sub-types provide three options for relating the values from different data series. The first sub-type plots each series independently with the data value determining the vertical distance between each point and the horizontal axis. The second sub-type plots the series stacked on each other in a cumulative fashion with the data value of each series determining the vertical distance from the point to the sum of the values in all the previous series. For example, if the first series starts with values {3.9, 4.2, ...}, the second series with values {1.2, 3.5, ...}, and the third series with values {3.1, 1.9, ...}, then the point value for the second element of the third series will be plotted at 9.6 (since 9.6=4.2+3.5+1.9) along the vertical axis. The third sub-type plots each series based on the proportional contribution of the value to the total of all values in that category. Using the example above, the three values would be plotted at 0.4375, 0.8020, and 1 because the intervals between zero and each of these numbers is 0.4375=4.2/(4.2+3.5+1.9) for the first, 0.3645...=3.5/(4.2+3.5+1.9) for the second, and 0.1979...=1.9/(4.2+3.5+1.9) for the third, although, by default, these numbers are presented as percentages on the vertical (Y) axis.
Area plots do not have any pre-defined styles.

This screenshot shows a table of data and three area plots. The data consist of three series organized by row and starting with the words "Widgets", "Gadgets", and "Lumpets". Each of these series has values in five categories. The three graphs illustrate the three sub-types of area plots, with the series plotted independently in the left plot, stacked in the middle plot, and proportionately stacked in the right plot.
Each series in area plots can include three main elements and two error elements, although only the value element is necessary. The series can have a 'Name' element, which is a single text entry used to identify the series, must have a 'Values' element, which is a sequence of numeric values, and may have a 'Label' element, which is a sequence of text entries used to identify the categories. All of these elements can be defined as references to a region of the worksheet, as literally defined entries, or as formula expressions which result in the correct type. The 'Label' element is shared by all of the series. The legend added to an area plot identifies the different series, by default using the entries of the 'Name' element of each series. The two error elements include a list for errors in the positive direction and one for errors in the negative direction.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. These will be used in the legend which may be displayed with the area plot. | {"Widgets"} |
| Value | A series of numeric values. | {1293, 2502, 3297, 1100, 2487} |
| Label | A series of textual elements labeling each value. Generally, this series will have as many entries as there were in the "Value" series. These entries are shared by all the series in the area plot. | {"North", "South", "Central", "East", "West"} |
| Error (+) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| Error (-) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
Area plots provide three icons to choose one of the three area plot sub-types.
-

-
The icon for an area plot of the sub-type with independent, overlapping areas.
-

-
The icon for an area plot of the sub-type with stacked areas.
-

-
The icon for an area plot of the sub-type with stacked, proportionate areas.
10.3.2. Bar Plots
Bar plots present the numeric values of categorical data with the data values of each series represented as a horizontal bar. Sequential data values are considered to belong to different categories and are plotted along the vertical axis at equally spaced intervals. The data values from different series are assigned to these categories based on the position of the value in the series, for example, the second data value taken from each series all share one category. The data values are plotted along the horizontal (X) axis as bars of different lengths and positions depending on the numeric content of the data value and the particular sub-type chosen for the bar plot.
Bar plot sub-types provide three options for relating the values from different data series. The first sub-type plots each series independently in adjacent bars, each of which is tied to the vertical axis and has its length determined by the numeric content of the data value. The second sub-type plots each series as a horizontally stacked set of bars with the horizontal length of each element determined by the numeric content of the data value and the position of the bar determined by the position of the element in the data series. For example, if the first series starts with values {3.9, 4.2, ...}, the second series with values {1.2, 3.5, ...}, and the third series with values {3.1, 1.9, ...}, then the third bar will be plotted ranging from 7.7 to 9.6, since 7.7=4.2+3.5 and 9.6=4.2+3.5+1.9. The third sub-type plots each series as a horizontally stacked set of bars scaled to the total all the numeric values in that category. Using the example above, the three bars would range from 0 to 0.4375, from 0.4375 to 0.8020, and from 0.8020 to 1 respectively because the intervals are the proportional contribution of each data value to the total, i.e. 0.4375=4.2/(4.2+3.5+1.9) for the first, 0.3645...=3.5/(4.2+3.5+1.9) for the second, and 0.1979...=1.9/(4.2+3.5+1.9) for the third. By default, these numbers are presented as percentages on the horizontal (X) axis.
Bar plots do not have any pre-defined styles.
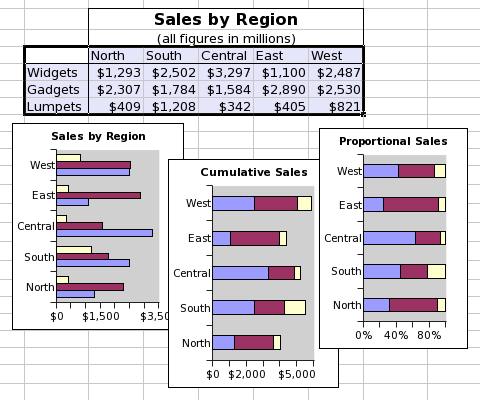
This screenshot shows a table of data and three bar plots. The data consist of three series organized by row and starting with the words "Widgets", "Gadgets", and "Lumpets". Each of these series has values in five categories. The three graphs illustrate the three sub-types of bar plots, with the series plotted independently in the left plot, stacked in the middle plot, and proportionately stacked in the right plot.
Each series in bar plots can include three main elements and two error elements, although only the value element is necessary. The series can have a 'Name' element, which is a single text entry used to identify the series, must have a 'Values' element, which is a sequence of numeric values, and may have a 'Label' element, which is a sequence of text entries used to identify the categories. All of these elements can be defined as references to a region of the worksheet, as literally defined entries, or as formula expressions which result in the correct type. The 'Label' element is shared by all of the series. The legend added to a bar plot identifies the different series, by default using the entries of the 'Name' element of each series. The two error elements include a list for errors in the positive direction and one for errors in the negative direction.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. These will be used in the legend which may be displayed with the bar plot. | {"Widgets"} |
| Value | A series of numeric values. | {1293, 2502, 3297, 1100, 2487} |
| Label | A series of textual elements labeling each value. Generally, this series will have as many entries as there were in the "Value" series. These entries are shared by all the series in the bar plot. | {"North", "South", "Central", "East", "West"} |
| Error (+) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| Error (-) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
Bar plots provide three icons to choose one of the three bar plot sub-types.
-

-
The icon for a bar plot of the sub-type with independent, adjacent bars.
-

-
The icon for a bar plot of the sub-type with horizontally stacked bars.
-

-
The icon for a bar plot of the sub-type with horizontally stacked, proportionately scaled bars.
10.3.3. Bubble Plots
The data values from three series of equal length are plotted on the Cartesian (X-Y) plane, the value from the first series determining the position of the plotted symbol center along the X axis, the value from the second series determining the position of the plotted symbol center along the Y axis, and the value of the third series determining the radius of the circle plotted. Each triplet of series can be plotted with different symbols but the data values of any series can be shared.
This screenshot shows a worksheet with a table of data with two series, each with three lists of numeric values. The screenshot also shows a bubble plot made from these two series.
Each series in a bubble plot can include four main components and four optional error components. The series may have a name, a single text value which will identify the series in the graph guru and in any legend attached to the chart. The series must have two lists of quantitative values, a list of X values and a list of Y values, which must have an equal number of elements. The series must also have a list, with the same number of elements, whose values will determine the size of the circles drawn at each point. The series may have lists of error components for the X values or the Y values and for positive or negative errors.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. | {"Series1"} |
| X | A list of numeric values, which will place the values along the horizontal axis. | {14.5, 2.8, 11.8, 5.7, 8.2} |
| Y | A second list of numeric values, which will place the values along the vertical axis. | {154, 29, 63, 90, 107} |
| Bubble | A series of numeric values, which will determine the size of each circle drawn at the points. | {45, 54, 34, 23, 37} |
| X Error (+) | A list of numeric values with as many elements as there were in the 'X' list. These values can be in the same units as the numeric values in the 'X' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| X Error (-) | A list of numeric values with as many elements as there were in the 'X' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
| Y Error (+) | A list of numeric values with as many elements as there were in the 'Y' list, and therefore in the 'X' list. These values can be in the same units as the numeric values in the 'Y' list, can be proportions or can be proportions multiplied by one hundred. | {0.09, 0.11, 0.10, 0.12, 0.09} |
| Y Error (-) | A list of numeric values with as many elements as there were in the 'Y' list, and therefore in the 'X' list. These values can be in the same units as the numeric values in the 'Y' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.09, 0.08, 0.11, 0.11} |
Bubble plots have a single icon for the plot style.
-

-
The icon for a bubble plot.
10.3.5. Column Plots
Column plots present the numeric values of categorical data with the data values of each series represented as a vertical column. Sequential data values are considered to belong to different categories and are plotted along the horizontal axis at equally spaced intervals. The data values from different series are assigned to these categories based on the position of the value in the series, for example, the second data value taken from each series all share one category. The data values are plotted along the vertical (Y) axis as columns of different heights and positions depending on the numeric content of the data value and the particular sub-type chosen for the column plot.
Column plot sub-types provide three options for relating the values from different data series. The first sub-type plots each series independently in adjacent bars, each of which is tied to the horizontal axis and has its height determined by the numeric content of the data value. The second sub-type plots each series as a vertically stacked set of columns with the vertical height of each element determined by the numeric content of the data value and the position of the column determined by the position of the element in the data series. For example, if the first series starts with values {3.9, 4.2, ...}, the second series with values {1.2, 3.5, ...}, and the third series with values {3.1, 1.9, ...}, then the third column will be plotted ranging from 7.7 to 9.6, since 7.7=4.2+3.5 and 9.6=4.2+3.5+1.9. The third sub-type plots each series as a vertically stacked set of columns scaled to the total all the numeric values in that category. Using the example above, the three columns would range from 0 to 0.4375, from 0.4375 to 0.8020, and from 0.8020 to 1 respectively because the intervals are the proportional contribution of each data value to the total, i.e. 0.4375=4.2/(4.2+3.5+1.9) for the first, 0.3645...=3.5/(4.2+3.5+1.9) for the second, and 0.1979...=1.9/(4.2+3.5+1.9) for the third. By default, these numbers are presented as percentages on the vertical (Y) axis.
Column plots do not have any pre-defined styles.
This screenshot shows a table of data and three column plots. The data consist of three series organized by row and starting with the words "Widgets", "Gadgets", and "Lumpets". Each of these series has values in five categories. The three graphs illustrate the three sub-types of column plots, with the series plotted independently in the left plot, stacked in the middle plot, and proportionately stacked in the right plot.
Each series in column plots can include three main elements and two error elements, although only the value element is necessary. The series can have a 'Name' element, which is a single text entry used to identify the series, must have a 'Values' element, which is a sequence of numeric values, and may have a 'Label' element, which is a sequence of text entries used to identify the categories. All of these elements can be defined as references to a region of the worksheet, as literally defined entries, or as formula expressions which result in the correct type. The 'Label' element is shared by all of the series. The legend added to a column plot identifies the different series, by default using the entries of the 'Name' element of each series. The two error elements include a list for errors in the positive direction and one for errors in the negative direction.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. These will be used in the legend which may be displayed with the column plot. | {"Widgets"} |
| Value | A series of numeric values. | {1293, 2502, 3297, ,1100, 2487} |
| Label | A series of textual elements labeling each value. Generally, this series will have as many entries as there were in the "Value" series. These entries are shared by all the series in the column plot. | {"North", "South", "Central", "East", "West"} |
| Error (+) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| Error (-) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
Column plots provide three icons to choose between three plot sub-types.
-

-
The icon for pie plot of style with joint slices.
-

-
The icon for pie plot of style with joint slices.
-

-
The icon for pie plot of style with joint slices.
10.3.8. Line Plots
Line plots present the numeric values of categorical data with the data values of each series connected by a line. Sequential data values are considered to belong to different categories and are plotted along the horizontal (X) axis at equally spaced intervals. The data values from different series are assigned to these categories based on the position of the value in the series, for example, the second data value taken from each series all share one category. The data values are plotted along the vertical (Y) axis according to their numeric value and the particular sub-type chosen for the line plot.
Line plot sub-types provide three options for relating the values from different data series. The first sub-type plots each series independently with the data value determining the vertical distance between each point and the horizontal axis. The second sub-type plots the series stacked on each other in a cumulative fashion with the data value of each series determining the vertical distance from the point to the sum of the values in all the previous series. For example, if the first series starts with values {3.9, 4.2, ...}, the second series with values {1.2, 3.5, ...}, and the third series with values {3.1, 1.9, ...}, then the point value for the second element of the third series will be plotted at 9.6 (9.6=4.2+3.5+1.9) along the vertical axis. The third sub-type plots each series based on the proportional contribution of the value to the total of all values in that category. Using the example above, the three values would be plotted at 0.4375, 0.8020, and 1 because the intervals between zero and each of these numbers is 0.4375=4.2/(4.2+3.5+1.9) for the first, 0.3645...=3.5/(4.2+3.5+1.9) for the second, and 0.1979...=1.9/(4.2+3.5+1.9) for the third, although, by default, these numbers are presented as percentages on the vertical (Y) axis.
Two styles are available by default for line plots. In the first no markers are placed on the value of the point whereas in the second a point marker is added wherever the points are plotted.
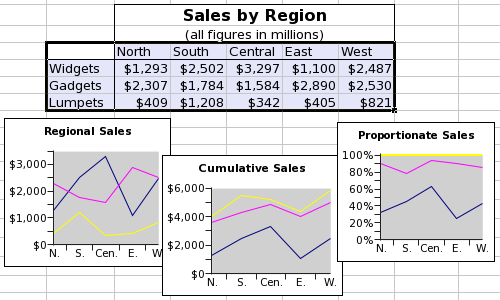
This screenshot shows a table of data and three line plots. The data consist of three series organized by row and starting with the words "Widgets", "Gadgets", and "Lumpets". Each of these series has values in five categories. The three graphs illustrate the three sub-types of line plots, with the series plotted independently in the left plot, stacked in the middle plot, and proportionately stacked in the right plot.
Each series in line plots can include three main elements and two error elements, although only the value element is necessary. The series can have a 'Name' element, which is a single text entry used to identify the series, must have a 'Values' element, which is a sequence of numeric values, and may have a 'Label' element, which is a sequence of text entries used to identify the categories. All of these elements can be defined as references to a region of the worksheet, as literally defined entries, or as formula expressions which result in the correct type. The 'Label' element is shared by all of the series. The legend added to a line plot identifies the different series, by default using the entries of the 'Name' element of each series. The two error elements include a list for errors in the positive direction and one for errors in the negative direction.
| Element | Type | Example |
|---|---|---|
| Name | A single textual entry labeling the data series. These will be used in the legend which may be displayed with the line plot. | {"Widgets"} |
| Value | A list of numeric values. | {1293, 2502, 3297, 1100, 2487} |
| Label | A list of textual entries labeling each value. Generally, this series will have as many entries as there were in the 'Value' series. These entries are shared by all the series in the line plot. | {"North", "South", "Central", "East", "West"} |
| Error (+) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| Error (-) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
Line plots provide six icons to choose between three plot sub-types each with two different styles.
-

-
The icon for a line plot of the sub-type with independent, overlapping lines and of the style without point markers.
-

-
The icon for a line plot of the sub-type with stacked lines and of the style without point markers.
-

-
The icon for a line plot of the sub-type with stacked proportion lines and of the style without point markers.
-

-
The icon for a line plot of the sub-type with overlapping lines and of the style with point markers.
-

-
The icon for a line plot of the sub-type with stacked lines and of the style with point markers.
-

-
The icon for a line plot of the sub-type with stacked proportion lines and of the style without point markers.
10.3.10. Pie Plots
Pie plots present the numeric values from a single series of categorical data as slices of a circular area, the angular arc of each slice determined by the proportional magnitude of each value compared to the overall sum of all the values. For example, if the series had values { 1.12, 4.48, 3.36, 1.68, 0.56}, the contribution of each slice to the total would be {0.10, 0.40, 0.330, 0.15, 0.0 5}, since 0.10= 1.12/(1.12+4.48+3.36+1.68+0.56), and the angular arcs of the wedges would be {36, 144, 108, 54, 18} degrees, since 36=0.10*360.
Pie plots do not have any sub-types.
Pie plot styles provide two choices for the rendering of the pie chart, either with all slices linked into one overall circle, or with gaps between the slices. The size of the gap is a property of the pie plot which can be changed.
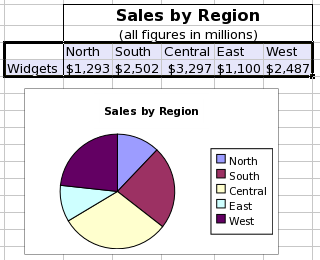
This screenshot shows a table of data and a pie plot. The data consist of a single data series organized in a row and starting with the word "Widgets". The series has values in five categories. The legend includes the names of the different data categories.
Each pie plot contains a single series which can include three elements although only the value element is necessary. The series can have a 'Name' element, which is a single text entry used to identify the series, must have a 'Values' element, which is a sequence of numeric values, and may have a 'Label' element, which is a sequence of text entries used to identify the categories. All of these elements can be defined as references to a region of the worksheet, as literally defined entries, or as formula expressions which result in the correct type. The legend added to a pie plot identifies the different categories using the entries in the 'Label' element.
| Element | Type | Example |
|---|---|---|
| Name | A single textual entry labeling the data series. | {"Widgets"} |
| Value | A list of numeric values. | {1293, 2502, 3297, 1100, 2487} |
| Label | A list of textual entries labeling the category of each value. Generally, this series will have as many entries as there were in the 'Value' list. These will be used in the legend which may be displayed with the pie plot. | {"North", "South", "Central", "East", "West"} |
Pie plots do not have any sub-types but provide two icons to distinguish the style of the plot allowing a choice between pie plots which comprise a single circular area or plots with distinct pie slices separated by small gaps.
-

-
The icon for a pie plot of the style with joint slices.
-

-
The icon for a pie plot of the style with separated slices.
10.3.12. Radar Plots
Radar plots present the numeric values of categorical data as a set of points plotted along a set of axes radiating from a central point, with as many axes as there are values in the series and with the points connected by a line, possibly with the interior of the shape filled in. Sequential data values are considered to belong to different categories and are plotted on separate axes which are not necessarily orthogonal and radiate from a central point. Sequential points are connected by a line with the final point connected back to the first to form a closed polygon. The data values from different series are assigned to categories based on the position of the value in the series, for example, the second data value taken from each series all share one category and will therefore all be plotted on the same axis. The data values are plotted along the axis of each class according to their numeric value.
Radar plots do not have any sub-types.
Radar plot styles provide three choices for the rendering of the chart. The first style presents the radar chart as only a polygon of lines. The second style also includes a marker where the data values are plotted on each axis. The third style plots the radar chart as a filled polygon.
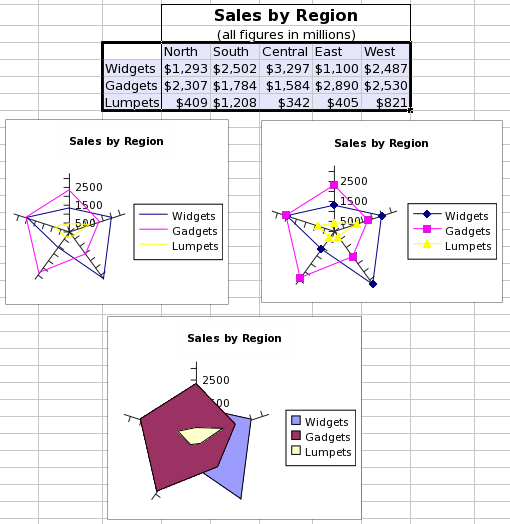
This screenshot shows a table of data and three radar plots. The data consist of three series organized by row and starting with the words "Widgets", "Gadgets", and "Lumpets". Each of these series has values in five categories. The three graphs illustrate the three sub-types of radar plots, with the top left plot including lines only, the top right plot including both lines and markers on the points, and the bottom middle plot using filled polygons.
Each series in radar plots can include three main elements and two error elements, although only the value element is necessary. The series can have a 'Name' element, which is a single text entry used to identify the series, must have a 'Values' element, which is a sequence of numeric values, and may have a 'Label' element, which is a sequence of text entries used to identify the categories. All of these elements can be defined as references to a region of the worksheet, as literally defined entries, or as formula expressions which result in the correct type. The 'Label' element is shared by all of the series. The legend added to a radar plot identifies the different series, by default using the entries of the 'Name' element of each series. The two error elements include a list for errors in the positive direction and one for errors in the negative direction.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. | {"Widgets"} |
| Value | A series of numeric values. | {1293, 2502, 3297, 1100, 2487} |
| Label | A series of textual elements labeling each value. Generally, this series will have as many entries as there were in the 'Value' series. | {"North", "South", "Central", "East", "West"} |
| Error (+) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| Error (-) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
Radar plots provide three icons distinguishing the three different styles.
-

-
The icon for a radar plot with the style displaying simple lines only.
-

-
The icon for a radar plot with the style displaying both lines and point markers on the data values.
-

-
The icon for a radar plot with the style displaying a filled area.
10.3.13. Ring Plots
Ring plots present the numeric values of categorical data as segments of circular rings. Sequential data values are considered to belong to different categories and are plotted with distinct patterns. The data values from different series are assigned to these categories based on the position of the value in the series, for example, the second data value taken from each series all share one category. The data values are used to determine the size of the arc based on the proportionate size of the data value to the sum of all data values in the series. For example, if the series had values { 1.12, 4.48, 3.36, 1.68, 0.56}, the contribution of each ring section to the total would be {0.10, 0.40, 0.330, 0.15, 0.0 5}, since 0.10= 1.12/(1.12+4.48+3.36+1.68+0.56), and the angular arcs of the sections would be {36, 144, 108, 54, 18} degrees, since 36=0.10*360.
Ring plots do not have any sub-types.
Ring plot styles provide two choices. Ring plots can be plotted with all segments linked into a single overall ring, with different series plotted immediately adjacent to one another in sequentially larger rings. Alternatively, the segments of the outermost ring can be split and float a certain distance away from the next ring.

This screenshot shows a table of data and two ring plots. The data consist of a single data series organized in a row and starting with the word "Widgets". The data consist of three series organized by row and starting with the words "Widgets", "Gadgets", and "Lumpets". Each of these series has values in five categories. The two graphs illustrate the two sub-types of ring plots, the left most plot without any gaps and the right most plot having the outer plot with gaps.
Each series in ring plots can include three main elements and two error elements, although only the value element is necessary. The series can have a 'Name' element, which is a single text entry used to identify the series, must have a 'Values' element, which is a sequence of numeric values, and may have a 'Label' element, which is a sequence of text entries used to identify the categories. All of these elements can be defined as references to a region of the worksheet, as literally defined entries, or as formula expressions which result in the correct type. The 'Label' element is shared by all of the series. The legend added to a ring plot identifies the different series, by default using the entries of the 'Name' element of each series. The two error elements include a list for errors in the positive direction and one for errors in the negative direction.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. | {"Widgets"} |
| Value | A series of numeric values. | {1293, 2502, 3297, 1100, 2487} |
| Label | A series of textual elements labeling each value. Generally, this series will have as many entries as there were in the "Value" series. | {"North", "South", "Central", "East", "West"} |
| Error (+) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| Error (-) | A list of numeric values with as many elements as there were in the 'Value' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
Ring plots provide two icons distinguishing the two different styles.
-

-
The icon for a ring plot with the style of displaying series in contiguous rings.
-

-
The icon for a ring plot with the style of displaying the outermost series separated from the rest.
10.3.15. Surface Plots
Surface plots are used to plot (x,y ,z) points in three-dimensional space as a surface where z is interpreted as the height above the xy-plane. A Gnumeric chart of course shows the projection of this surface in 3-space onto a 2-dimensional sheet.
Surface plot sub-types provide for 2 distinct ways of providing the data for a surface plot.
The first subtype uses an n by 1 or 1 by n range for the x-values, a second 1 by m or m by 1 range for the y-values and an m by n range for the z values. The plotted points are constructed from these three ranges in such a way that the z value in the ith column and jth row is combined with the ith x value and the jth y value. This subtype then uses an m by n grid for the surface.
The second subtype uses a direct listing of the n points. The x values are specified with an n by 1 range, so are the y and z values. The ith z value is then combined with the ith x and ith y value to obtain the points to be plotted.It is not necessary to provide the same number of y coordinates for each x coordinate or vice versa. Gnumeric will interpolate missing values. For this purpose one needs to specify the number of (equidistant) rows and columns to be used for the surface grid. This grid need not align with the provided coordinates.
Surface plots do not have any pre-defined styles.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. These will be used in the legend which may be displayed with the surface plot. | {"Widgets"} |
| X | An optional series of numeric values to be used for the x coordinates of the grid. This defaults to {1,2,…,n}. | {1,3,5,6,8,9} |
| Y | An optional series of numeric values to be used for the y coordinates of the grid. This defaults to {1,2,…,n}. | {1,1.5,2,2.5} |
| Z | A rectangular range of numbers where the number in jth row and ith column is the height of the (i,j) grid point. | A2:J15 |
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. These will be used in the legend which may be displayed with the surface plot. | {"Widgets"} |
| X | A series of numeric values to be used for the x coordinates of the grid. | {1,1.5,2,2.5} |
| Y | A series of numeric values to be used for the y coordinates of the grid. | {1,1.5,2,2.5} |
| Z | A series of numeric values to be used for the z coordinates of the grid. | {1,1.5,2,2.5} |
Surface plots provide two icons to choose one of the two surface plot sub-types.
-

-
The icon for an area plot of the sub-type with rectangular data area.
-

-
The icon for an area plot of the sub-type with xyz series.
10.3.16. XY Scatterplots
The data values of two series of equal length are plotted on the Cartesian (X-Y) plane, the value from the first series determining the position of the plotted symbol along the X axis, and the value from the second series determining the position of the plotted symbol along the Y axis. Data can be plotted as points only, with each pair of data series having different symbols, or, alternatively, sequential data pairs can be connected by a line, or, finally, both symbols and a connecting line can be used.
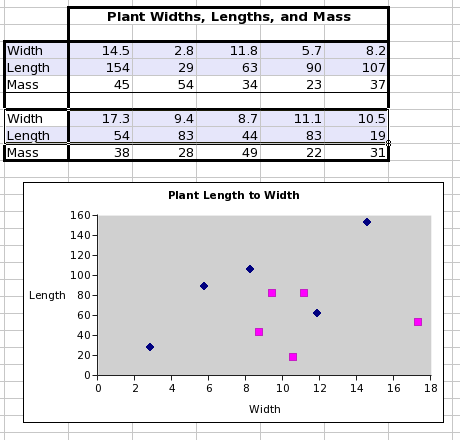
This screenshot shows a data table with two different series highlighted which are usable in a scatterplot. Each series is comprised of two lists of numeric values. The screenshot also shows the scatterplot made from these two data series.
Each series in a scatterplot can include three core components and four optional error components. The series may have a name, a single text value which will identify the series in the Graph Guru and in any legend attached to the chart. The series must have two lists of quantitative values, a list of X values and a list of Y values, which must have an equal number of elements. The series may also contain lists of error values for each of the X and Y lists with a positive and a negative component for each.
| Element | Type | Example |
|---|---|---|
| Name | A single textual element labeling the data series. | {"Series1"} |
| X | A list of numeric values, which will place the values along the horizontal axis. | {14.5, 2.8, 11.8, 5.7, 8.2} |
| Y | A second list of numeric values, which will place the values along the vertical axis. | {154, 29, 63, 90, 107} |
| X Error (+) | A list of numeric values with as many elements as there were in the 'X' list. These values can be in the same units as the numeric values in the 'X' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.12, 0.09, 0.11, 0.09} |
| X Error (-) | A list of numeric values with as many elements as there were in the 'X' list. These values can be in the same units as the numeric values in the 'Value' list, can be proportions or can be proportions multiplied by one hundred. | {0.08, 0.11, 0.10, 0.09, 0.11} |
| Y Error (+) | A list of numeric values with as many elements as there were in the 'Y' list, and therefore in the 'X' list. These values can be in the same units as the numeric values in the 'Y' list, can be proportions or can be proportions multiplied by one hundred. | {0.09, 0.11, 0.10, 0.12, 0.09} |
| Y Error (-) | A list of numeric values with as many elements as there were in the 'Y' list, and therefore in the 'X' list. These values can be in the same units as the numeric values in the 'Y' list, can be proportions or can be proportions multiplied by one hundred. | {0.10, 0.09, 0.08, 0.11, 0.11} |
XY scatterplots provide three icons to select between different style options. The plots can be rendered with markers at each point, with markers at each point and a line joining adjacent values in the data lists, or with a line but no markers.
-

-
The icon for scatterplot of style with only a marker at each point.
-

-
The icon for scatterplot of style with a marker at each point and a line between adjacent points in the value lists.
-

-
The icon for scatterplot of style with only a line between adjacent points in the value lists.
10.4. Configuring Graph Element Properties
Graphs in Gnumeric can be configured extensively using the Graph Guru. In this way, the user can determine the data used in the plots, the names and labels associated with the data, the numerical values of the axes and the stylistic presentation of all the graphical elements.
Graphs are configured element by element, first by selecting the element name in the top left area of the second panel of the Graph Guru, shown as area in Figure 10-3, and, second, by altering the properties in the bottom area of the second panel of the Graph Guru, shown as area . These changes will be applied to the graph only when the button is pressed.
A number of properties of the graph are configured using the Gnumeric entry box shown in Figure 10-15.
Information can be inserted to the data entry box, first, by selecting the box with a mouse click and, then, either typing data on a keyboard or using the mouse to select a region of the worksheet.- 10.4.1. Background Panels: Graphs & Charts
- 10.4.2. Titles and Axis Labels
- 10.4.3. Chart Legends
- 10.4.4. Axes
- 10.4.5. Plots
- 10.4.6. Data Series
10.4.1. Background Panels: Graphs & Charts
Several elements of the graph function as background panels for the other elements. These panels can be configured to display a visible background consisting of a solid color, a pattern, a gradient, or an image. Alternatively, the panel can be made transparent to show the underlying panel, if any. Where there are only transparent panels, the worksheet itself will be visible behind the graph.

This screenshot depicts the two elements of background panels which can be configured, the background fill and the outline.
The background panel Fill refers to the area which is behind the entire component. The Outline refers to a solid box which will be drawn around the edge of the component.
The Outline can be configured by selecting a color using the color picker widget and by choosing a size using the spin button box. A size of '-1' indicates that no line will be drawn, whereas sizes zero and above indicate the size of the line that will be drawn.
The Fill can be configured to be a pattern, which includes a solid color, a gradient or an image.

This screenshot depicts the configuration properties for the pattern background panel fill.
The fill using a pattern enables the panel background to consist either of a solid color, or of a solid color overlain by a pattern. The top drop down button, labeled Pattern, allows the user to select the pattern overlay from a number of different standard patterns. The pattern in the top left corner is an empty pattern which allows the background color indicated in the third drop down button to fill the panel. The middle drop down button, labeled Foreground, allows the user to select the color of the overlay in the pattern. The bottom drop down button, labeled Background, allows the user to select the color of the underlay. If the pattern is empty, the color of the Background will be the color of the entire panel.
If all of these buttons appear black, change the color of the Background to white to see the pattern and foreground color.
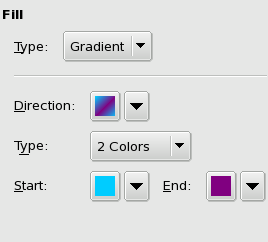
This screenshot depicts the configuration properties for the gradient background panel fill.
The background panel can be filled with a gradient transitioning either between two colors or between a color and a tone, either white or black. The top drop down button, labeled Direction, gives the user a number of choices for the direction in which the gradient will operate. The drop down button named Type allows the user to pick between gradients which transition between two colors, the 2 Colors option, and gradients that transition from a color to pure white or pure black, the Brightness option. The drop down buttons for the Start and End colors allow the user to pick the colors in the gradient. For the brightness gradients, a slider allows the user to select the transition direction. Moving the slider toward Brighter will fade the color to white whereas moving the slider toward Darker will fade the color toward black.
If all of these buttons appear black, change the color of the Start button to white to see the gradient.
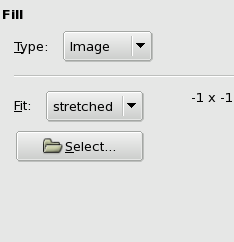
This screenshot depicts the configuration properties for the image background panel fill.
The image background fill type allows the user to select an image to fill the background of the panel. The image can be in any file format supported by the gdk-pixbuf library as explained in Section 9.2 ― Images. The image can be fit in one of two ways. The image fit can be stretched so the image fills the whole panel area or the image fit can be wallpapered where the image is repeated in a tile pattern to fill up the whole background. The button labeled Select allows the user to call the file selector and choose the file which contains the desired image. On the GNOME desktop, the file chooser has a preview area to see the image before adding it. The size of the image, in pixels, is displayed in the configuration dialog as '# x #' where the number symbol indicates the number of pixels, and the number of pixels in each row comes before the number in each column.
10.4.2. Titles and Axis Labels
Both Title and Axis Labels can be configured using three tabs. The first tab allows the user to configure the background panel of the title or axis label. The second tab allows the user to select the font that will be used to display the words in the title or axis label. The third tab allows the user to input the actual words which will be used in the graph.
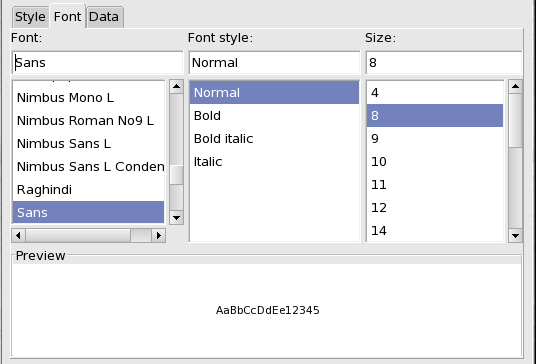
This screenshot depicts the font configuration panel for titles and axis labels in the Graph Guru.
The Style tab allows the user to configure the background panel in the same way this was configured for graphs, charts and grids, as was explained above in Section 10.4.1 ― Background Panels: Graphs & Charts.
The Font tab is shown in Figure 10-20 and consists of three column lists. The first column list allows the user to select the font name by scrolling the list and then clicking on the desired name. The currently selected font name is highlighted in light blue. The second column list allows the user to select the font style including italic and bold styles. The third column list allows the user to select a size for the font. The preview area contains a few characters to illustrate the appearance of the currently selected combination.
The Data tab displays a single entry box in which the user can place the words which will appear in the title or in the label. The user can simply type the text, can add a reference to a section of the worksheet or can add an expression which results in a text value.
10.4.3. Chart Legends
Chart legends provide a graphical explanation of the data plotted with the names and style of the different series, or categories, plotted in each chart. Legends are configured through two tabs, labeled Style and Font. The Style tab allows for the configuration of the background pane in a manner analogous to the graph, chart and grid background panes, explained in Section 10.4.1 ― Background Panels: Graphs & Charts. The Font tab allows the configuration of the font that will appear in the legend. This configuration is identical to the configuration of the title and axis label fonts presented in Section 10.4.2 ― Titles and Axis Labels.
10.4.4. Axes
Axes are used in several different kinds of plots to provide quantitative indexes for the scale of each plot direction. Gnumeric uses four different kinds of axes. Category axes do not provide a quantitative scale but merely distinguish each different category by providing space for the values of the category along the axis. Continuous axes provide a quantitative measure of each value based on the projection of that value onto the axis. Radial axes are used in radar plots and are continuous axes which radiate from a central point. Circular axes have not yet been implemented.
Line, column and area charts use a category axis to separate the categories along the horizontal direction and a continuous axis to distinguish values in the vertical direction. Bar charts reverse these two axes. XY scatter plots and bubble plots use two continuous axes, one in the horizontal direction, the X-axis, and one in the vertical direction, the Y-axis. Radar plots use three or more continuous axes radiating from a central point. Pie and Ring plots do not use any axes.
- 10.4.4.1. Category Axes
- 10.4.4.2. Continuous Axes: Linear, Radial & Circular
- 10.4.4.3. Grids
10.4.4.1. Category Axes
Category axes distinguish the different categories of each value in a category series such as the series in line, bar, column and area plots.
The Bounds tab allows the user to override the automatic configuration of axis tick marks and labels. Each of the three choices can be over-ridden by deselecting the check box on the left. The check boxes can be deselected by placing the mouse pointer over the check box and clicking with the primary mouse button. When a check box is unselected, the entry box will become active allowing the user to input a different value than the default. The first check box controls the number of tick marks, allowing tick marks to appear after the integer number of categories shown. The second check box controls the number of labels displayed, allowing a regular number of category labels to be skipped. The third check box controls the placement of the orthogonal axis relative to the category axis.
The Style tab allows the user to configure the line style of the axis, including the color and thickness of the line. The drop down button labeled Color can be clicked to expose the color picker panel which allows the user to select a new color either simply by clicking on an icon or by using the color picker wheel. The size spin button allows a user to change the thickness of the axis by typing a new number in the text box or by clicking on the arrows. A value of '-1' in this box will cause the axis not to be drawn.
The Font tab allows the user to configure the font used to label the separate categories. The font configuration is performed in the same way as the font configuration for titles and axis labels which was explained in Section 10.4.2 ― Titles and Axis Labels.
The Details tab allows a user to configure other aspects of the axis.
The Position of the axis is placed in the Low position by default. This can be altered by pressing the radio button in front of the High label which will move the internal button and will alter the position of the axis, moving it either to the top of the graph for horizontal axes, or to the right of the graph for vertical axes.
The Mapping of the axis can be changed simply by clicking on the check box. This will cause a check mark to appear in the box and will invert the axis so that the order of the categories will become reversed.
The Major ticks displayed on the axis can be altered. The labels shown in the plot can be hidden by unchecking the check box in front of the 'Show Labels' text by placing the mouse cursor over the box and clicking with the primary mouse button. The ticks on the axis can be hidden or can be displayed on the outside of the graph, or on the inside of the graph, or on both sides depending on which of the two boxes are checked.
The Minor ticks do not currently have any effect for category axes.
10.4.4.2. Continuous Axes: Linear, Radial & Circular
Continuous axes are configured in much the same way as category axes except for some minor differences.
The Bounds tab allow users to configure the limits and intervals of a continuous axis. The meaning of the values for Major Ticks and Minor Ticks depends on the type of continuous axes:
- Continuous Axes with Linear Scale
-
The Major Ticks value gives the distance between major ticks and the Minor Ticks value the distance between minor ticks.
- Continuous Axes with Logarithmic Scale
-
The Major Ticks value gives the number of decades (powers of 10) between major ticks. The Minor Ticks value gives the number of minor ticks between major ticks.
If the Major Ticks value is N, then the Minor Ticks value can be 0, N−1, or 9N−1.
The Style tab changes the linear style of the axis in the same way as it acted on category axes. The explanation given in Section 10.4.4.1 ― Category Axes apply equally well to continuous axes.
The Font tab also allows users to configure the font used in the numeric markers along the axis. Selecting the font for a continuous axis works in the same way as for a category axis as was explained in Section 10.4.4.1 ― Category Axes.
The Details tab has two small differences compared to category axes. The mapping of the axis can be altered from a linear scale to a logarithmic scale by clicking on the drop down box and dragging to the entry labeled . The minor ticks, whose size was configured in the Bounds tab, are displayed for continuous axes unlike for categorical axes.
The Format tab allow users to configure the numeric type of the elements on a continuous axis. This configuration parallels the configuration of the numeric type of a worksheet cell as explained in Section 5.10.1 ― Number Formatting Tab.
10.4.4.3. Grids
Users can add both major and minor grids to an axis. Grids are lines that are perpendicular to the axis at fixed intervals. An example of major (in blue) and minor (in green) grids attached to a vertical axis are shown in Figure 10-26.
To add either a major or minor grid to an axis, the user selects the appropriate axis in the hierarchy tree of graph components, clicks the button below the hierarchy, and selects either or .
When a grid has been added to an axis, it can be selected in the hierarchy tree of graph components and customized in its configuration tab. One can specify the style, color, and thickness (size) of the grid lines as well as specify a fill to be applied to the space between every second pair of consecutive grid lines.
10.4.5. Plots
Certain of the properties of plots are assigned directly to the plot element and are configured when the plot element itself is selected.
Line plots, Area plots, and XY scatter plots do not have any plot level properties which can be configured.
- 10.4.5.1. Bubble plots
- 10.4.5.2. Pie plots
- 10.4.5.3. Bar and Column plots
- 10.4.5.4. Radar plots
- 10.4.5.5. Ring plots
10.4.5.1. Bubble plots
The bubbles in bubble plots are used to represent a third data component with the size of the bubble representing the value of the third component.
The first choice in the bubble plot properties allows the user to represent the bubble value based on the area or the diameter of the bubble. The representation of a bubble using the surface is similar to using a log scale since the area is a squared quantity.
The Show negative values property, if the check box is checked, will cause negatives values to be shown with the size of the bubble based on the absolute value of the value and the style of the bubble having a white fill.
The Vary colors by bubble, if the check box is checked, will cause each value in a series to be displayed with a different fill color instead of coloring all the values in a single series with the same color.
The bubbles in a series are scaled relative to each other with the maximum value having a default, fixed size and the other values being scaled to this maximum bubble. Using this spin button, the default size of the maximum bubble can be altered.
10.4.5.2. Pie plots
Pie plots represent the data values as slices of a circular area, with the central angle of each slice, or wedge, proportional to the size of the value compared to the sum of all the values in the series.
The slices by default are plotted clockwise starting from the vertical which is considered 0 degrees. The first option allows the user to set a different starting point for the pie series by changing the value in the spin box. The value will increase to 360 degrees and then reset to zero.
Pie plots can be displayed with the slices separated from each other which in certain situations may improve the visual clarity of a pie plot. The second spin button allows the slices to be separated.
The colors of each slice, by default, are all different to allow the easy visual distinction between each slice. Since pie plots only allow a single series to be plotted, there is no need to use color to associate the values from different series. By unchecking this box, all of the slices in a pie chart can be made to follow the color scheme defined in the plot series Style tab. However, if this box is unchecked, the outlines of the slices must be styled with a different color for the slices to be distinguishable.
10.4.5.3. Bar and Column plots
Bar and column plots can be displayed with different sized gaps between categories and different overlaps between the values of different series in each category.
The Gap describes the separation between the values plotted in each category. By default, the gap between categories is one and half times the width of a bar or a column. This spin button can be used to decrease the gap to zero, so there is no gap between categories, or increase the gap to 500% so the gap is five times the size of a bar or a column.
The Overlap describes the separation between values of the different series in each category. By default these values will be plotted immediately adjacent to each other. This spin button can be lowered to minus 100% which leaves a gap the size of a bar or column between the values of each series. Alternatively, the values can be made to overlap up to 100%, a complete overlap. When values completely overlap, the latter series are plotted on top of the first series and a value may be completely obscured. In this case it may be possible to use partially transparent colors for the different series to allow both values to be visible.
10.4.5.4. Radar plots
Radar plots have as many axes as there are categories in each series.
By default the axis for the first category is vertical leaving the center point in the upward direction. The first spin box in the radar plot properties allows a user to change this orientation. The spin button can increase from zero degrees to 359 degrees when it will reset to 0.
The Vary colors by slice property is probably a mistake which should not be part of radar plot properties.
10.4.5.5. Ring plots
Ring plots are similar to pie plots but may have an empty center and can be made with multiple series.
Like pie plots, ring plots assign values to the slices of a circular area by representing the magnitude of the value by the central angle of the slice, although for ring plots the center of the circular area is empty. Like pie plots, the first slice is plotted starting clockwise from the vertical and this first option can change the beginning point of the first slice's angle.
The slices of a ring plot can also be separated. The Slice Separation option allows a user to determine the proportional size of the gap between slices.
The Center size option determines the size of the hole in the middle of the rings as a fraction of the total radius. The center size can be altered in 5 percent increments.
The Vary colors by slice check box allows the user to assign colors either by slices, which is the default, or by series. To use color to distinguish series rather than categories, this button should not be checked.
10.4.6. Data Series
Each plot will have one or more 'series' which organize the data values. Each series element has a number of properties. The element will have a Style tab with which the style of the line and point markers, or the area and outline can be set. Each series element will have a Data tab in which the name of the series, the values used for the series and any labels associated with these values can be entered. The data values will generally be entered as references to cells on a worksheet which will allow the plots to be automatically altered when the values in the worksheet change. The series may also have one or more Error tabs in which error values can be associated to the data value of each element in the series.
- 10.4.6.1. Series line style
- 10.4.6.2. Series filled style
- 10.4.6.3. Series data: single values
- 10.4.6.4. Series data: X and Y values
- 10.4.6.5. Series data: bubble values
- 10.4.6.6. Series error values
10.4.6.1. Series line style
Series in line plots, in some radar plots and in scatter plots will have a style tab in which the graphical style of the lines and point markers can be established.
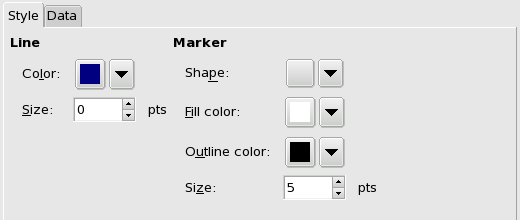
The properties of a single value data series include an optional name, a required list of values and an optional list of labels. The name, in this case, is a reference to cell D7 in the first worksheet. The values are the contents of the cells in the range E7:I7. The labels are the contents of the cells in the range E6:I6. Note that there are as many cells in the labels range as in the values range.
The Line properties include the line color and size. The color can be altered in the standard way using the drop down color chooser. The width of the line can be changed with the spin box. A line size of '-1' means that the line will not be plotted.
The Marker properties determine the style of the graphical symbol which will be plotted for each data value. The first drop down box allows the user to choose between a number of different symbols. The blank symbol indicates that no symbol will be plotted where the data value would be. Each shape will have a fill color, and an outline with both a color and a size. The colors can be changed by clicking on the drop down box and picking one of the given colors or using the color picker to select a new color. The size of the outline can be altered by clicking in the text area and editing the value or by using the spin arrows to increase or decrease the size.
10.4.6.2. Series filled style
Series in bubble plots, area plots, bar plots, column plots, filled radar plots, and ring plots will have a Style with fill and outline properties. These properties are the same as those presented for background panels in Section 10.4.1 ― Background Panels: Graphs & Charts and are changed in the same way.
The Fill properties will determine the character of the inside of the area. The fill type can be none, pattern, gradient, or image, in the same way as the fill of background panels. If images are used for the background, the whole image will be shown and it will be scaled to the size of the area.
The Outline properties will determine the size of the linear element that surrounds the area. The color and size of this outline element can be altered.
10.4.6.3. Series data: single values
The Data tab allows the user to configure the data contents of the series. Some of these data contents are optional, as is indicated by the parentheses around the label. At the minimum one set of numerical quantities will be required.
The entry boxes in the Data tab can be filled in several ways. The data can be a static value or array such as a sting literal, "SeriesName", or a group of values, {12.05, 73.02, 128.89}. Note that the separator between elements in the array will depend on the locale since the glyph between whole numbers and decimal fractions differs around the world. Alternatively, the value of an entry box can be the reference to a cell or to a range. This reference can either be typed into the entry box or can be entered by clicking in the entry box text area and then selecting the range on the worksheet. Finally, the value in the entry box can be an expression, such as sin({120, 982, 140}).
Single series involve the simplest data. They may have an overall name, must have a list of values, and may have a list of names, with as many names as there are numbers in the values list, which will act as category names. For plot types with more than one single list series, the label names will be shared between all the series.
The Name property is a single string which will give a tag to the series itself. A name is not required. This name will be used in the Graph Guru to name the series and may be used in a chart legend to describe the series.
The Values property must contain a list of numeric quantities. A list of values is required. The values can be described either directly as a static array, described through a reference to a cell range with numeric values, or described through an expression which results in the list of quantities.
The Labels property describes the names of the categories. This property is not required. must be a list of text elements, with as many elements as there are quantities in the list of values. These elements will provide the elements in the legend for pie and ring plots. For line, area, bar and column plots, the labels will provide the category names for the axis with categories.
The Show in Legend property determines if this series will be shown in the legend if a legend is added to the chart. It is sometimes useful to exclude certain series from the legend. If the box is checked, the series will be included in any legend displayed in the chart; if the box is not checked, the series will not be displayed in the legend. The box can be unchecked by placing the mouse pointer over the box and clicking with the primary mouse button.
10.4.6.4. Series data: X and Y values
Series with dual data values allow plots to be constructed in which one value is plotted against the other. XY scatter plots require this type of data.
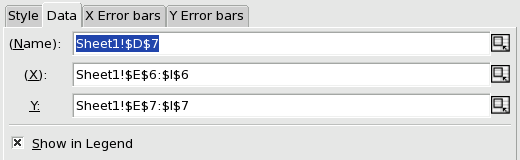
Dual data series require two sets of values, an X list and a Y list.
The Name property is a single text element that will name the series in the graph guru and in any legend in the chart.
The X property is a list of quantitative values that will provide the horizontal positioning of each element. This list is required.
The Y property is a list of quantitative values that will provide the vertical positioning of each element. This list is required and must have the same number of elements as the list of X values.
10.4.6.5. Series data: bubble values
Bubble series are simple extensions of the XY series to include a third data value, often called W, which will determine the size of the bubble.
The Name property is a single text element that will name the series in the graph guru and in any legend in the chart.
The X property is a list of quantitative values that will provide the horizontal positioning of each element. This list is required.
The Y property is a list of quantitative values that will provide the vertical positioning of each element. This list is required and must have the same number of elements as the list of X values.
The Bubble property is a list of quantitative values that will provide the size of the bubbles associated to each element. This list is required and must have the same number of elements as the lists of X and of Y values.
10.4.6.6. Series error values
Several plot types allow the plotting of error values using whisker plots. The series in these plot types will have extra tabs allowing the whisker positions to be listed. Line, bar, column and area plots allow an error plot to bracket the plotted quantitative value in the direction of the quantitative axis. XY scatter plots and bubble plots allow whiskers in both directions.
The Error Category includes several different categories which can be selected by clicking on the drop down box and dragging the mouse pointer onto the appropriate entry. If the error category is set to "none", no error bars will be plotted. If the category is set to "absolute" the values in the error lists will be considered to be in the same units as the axis. If the category is set to "relative", the values in the error list are assumed to be a fraction of the total of each value. If the category is set to "percent", the values in the error list are assumed to be 1/100 th of the fraction of the total of each value. Note that if the cells in the worksheet are already set to the percent format, they should be incorporated as "relative" errors.
The Style properties alter the appearance of the error whiskers. The Display property can be used to prevent the display of any whiskers, to allow only upper or lower whiskers, or to display both. The Width property alters the width of the outer marker of the whisker. The Line width property alters the size of the whiskers. The color box selects the color of the line used to draw the whiskers.
The Values properties describe the lists of quantitative values which will be used for the whiskers. These lists are required if an error is to be displayed and the lists must have as many elements as were in the list of data "Values". The positive (+) list quantifies either only the upper error values if the lower values are not displayed or the negative list is defined. The positive list can also be used for both error values if the errors are symmetrical. The negative (-) list quantifies the lower whisker.
11. Using Worksheets
This chapter explains the use and manipulation of worksheets in Gnumeric. The chapter explains how to move around a worksheet, how to alter the appearance and display organization of the worksheet contents, how to manipulate entire worksheets and how to protect worksheet contents.
- 11.1. Worksheet Overview
- 11.2. Worksheet Navigation
- 11.3. Worksheet Display
- 11.4. General Settings
- 11.5. Print Settings
- 11.6. Managing Worksheets
11.1. Worksheet Overview
Worksheets contain the elements, such as the cell grid area, which provide the principal work entities for Gnumeric users. The worksheet grid area allows users to enter data, develop analyses of these data, and display both data and results. Worksheets also contain graphical elements such as graphs and widgets. Worksheets are grouped into a workbook which is stored in a Gnumeric file. The manipulation of workbooks is explained in Section 12.1 ― Overview while the material below explains the manipulation of worksheets.
Worksheets contain both working elements and metadata elements. The working elements include the data contents of cells in the grid area, cell comments, cell formatting, and sheet objects, such as graphical plots. The metadata include the worksheet name and worksheet settings controlling the visual appearance of the worksheet or the display of the worksheet.
This section explains the main ways to manipulate Gnumeric worksheets. Section 11.2 ― Worksheet Navigation explains how to navigate the worksheet to change the area which is displayed and change the currently selected area. Section 11.3 ― Worksheet Display presents several alternative settings which alter the display of cell contents, of the grid area, of the worksheet as a whole or of Gnumeric itself. Section 11.4 ― General Settings explains how to alter settings which affect all the contents of the worksheet such as the status of the content protection mechanism. Section 11.5 ― Print Settings gives a brief explanation of the print settings which apply specifically to each worksheet; a more complete explanation of the print settings is given in Chapter 15 ― Printing. Finally, Section 11.6 ― Managing Worksheets explains how the entire collection of worksheets can be manipulated so as to add, duplicate, delete or re-order the worksheets within a workbook.
11.2. Worksheet Navigation
Gnumeric worksheets can be conceived of as a single, continuous, two-dimensional grid of cells. However, Gnumeric cannot display the entire grid at once but only shows a portion of the worksheet. Since only a portion of the worksheet can be seen at any particular time, Gnumeric provides users with several ways to change the portion of the worksheet that is displayed. Section 11.2.2 ― Moving the Selection explains the various ways that the display window can be moved to a different section of the worksheet grid, while Section 11.3 ― Worksheet Display , further below, explains more powerful methods to re-organize the display of the cell grid area.
- 11.2.1. Moving Around a Worksheet
- 11.2.2. Moving the Selection
11.3. Worksheet Display
The display of each worksheet can be controlled by several settings and configurations. The worksheet, conceptually, consists of a single continuous two dimensional grid of cells arranged in rows by columns, and Gnumeric, by default, displays a small portion of the worksheet area as a continuous region.
A worksheet is created with the number of rows and columns specified by the preference setting that can be adjusted on the Windows tab of the Preference Dialog (see Section 13.2.7 ― Windows Preferences).
The maximum number of rows in a sheet is 16,777,216 and the maximum number of columns is 16384. The dimensions of a sheet can only be set to powers of 2.
The size of an existing sheet can be increased through the Resize Sheet dialog accessible through the sheet tab context menu (see Section 4.3.3 ― Context Menu for Worksheet Tabs) or the Sheet submenu of the Edit menu (see Section 4.2.4 ― Edit Menu).
- 11.3.1. Worksheet Appearance
- 11.3.2. Workbook Appearance
- 11.3.3. Grouping Rows and Columns
- 11.3.4. Display Panes
11.3.1. Worksheet Appearance
A number of aspects of how a worksheet is displayed in the cell grid can be modified. To adjust the display of formulas or results, A1 or R1C1 notation for cell references, how cells with a value of zero are displayed, the presence or absence of grid lines or row or column headers, or whether columns are ordered left to right or right to left, see the description of the Format ▶ Sheet submenu.
11.3.2. Workbook Appearance
This section has not yet been written.
- 11.3.2.1. Zoom: Changing the Scale of a Sheet
- 11.3.2.2. Full Screen Mode
- 11.3.2.3. Displaying Workbook Tabs
- 11.3.2.4. Displaying Grid Area Scrollbars
11.6. Managing Worksheets
This section discusses functions that manipulate worksheets as a whole, rather than their contents.
- 11.6.1. Worksheets and the Menubar
- 11.6.2. Worksheet Tab Context Menu
- 11.6.3. Manage Sheets dialog
- 11.6.4. Adding a Blank Worksheet
- 11.6.5. Copying or Pasting a Worksheet
11.6.1. Worksheets and the Menubar
Gnumeric provides a number of options for manipulating worksheets as a whole, rather than the contents of the worksheets. These operations are documented in the later section Section 11.6.2 ― Worksheet Tab Context Menu. In addition to the worksheet tab context menu and the submenu of the menu, some of these operations are also available from other menus:
- The Insert function is also available as on the menu.
- The Rename and Manage Sheets dialogs are also available on the submenu.
In addition to worksheet manipulation, Gnumeric provides the ability to control various aspects of how or whether a worksheet is displayed in the cell grid. Several such controls are included in the Section 11.6.3 ― Manage Sheets dialog, described in a later section. Other worksheet display controls are located in the Format ▶ Sheet submenu, which are described there.
11.6.2. Worksheet Tab Context Menu
Except for the addition of the two submenus, which appear only on the context menu, this is the same as the submenu. The dialog is discussed in Section 11.6.3 ― Manage Sheets dialog, which follows the description of the context menu.
- — Select this menu item to insert a new, empty worksheet ahead of the current worksheet. The new worksheet is the same size as the current one.
- — Select this menu item to add a new, empty worksheet at the end of the existing worksheets. The new worksheet has the default size, which can be set in the Gnumeric Preferences dialog in the “Windows” tab.
- — Select this menu item to add a copy of the selected worksheet immediately after the selected worksheet.
- — Select this menu item to delete the selected worksheet.
- — Select this menu item to access the Rename Sheet dialog, which lets you change the name of a single worksheet. To rename more than one worksheet, the Manage Sheets dialog may be more convenient.
- — Select this menu item to access the Resize Sheet dialog. Use the sliders to adjust the size of the sheet, then click OK. Worksheet dimensions are restricted to powers of two. By default the Resize Sheet dialog changes the sizes of all worksheets in the current workbook. To change the size of a single worksheet, clear the check mark next to Apply change to all sheets before clicking OK.
- and — Select one of these menu items to access a menu of worksheet names. Click on one of the names to select that worksheet. The displayed tabs are adjusted so that the selected worksheet's tab is visible, and the selected worksheet is displayed in the cell grid.
11.6.3. Manage Sheets dialog
The Manage Sheets dialog can be accessed from the worksheet tab context menu, from the submenu, or from the submenu.
The worksheets contained in the current workbook are listed in the upper left portion of the dialog. When Show advanced sheet properties is enabled, the Dir, Rows, and Cols fields are included. A worksheet can be selected by clicking anywhere in its line, although clicking one of the icons will toggle its associated property along with selecting the worksheet. Multiple selection, using the Shift and Ctrl keys, can be used to operate on more than one worksheet at a time. The current worksheet shown in the cell grid tracks the selected worksheet in this dialog. That is, selecting a single worksheet from the list also causes that worksheet to be displayed in the cell grid. When more than one worksheet is selected in the list, the first one in the list is set as the current worksheet in the cell grid. Some operations are not available when more than one worksheet is selected. The buttons for those operations are dimmed when they are unavailable.
The Lock column of the list shows an icon to indicate whether
the worksheet is locked,
![]() , or unlocked,
, or unlocked,
![]() . Click on the displayed icon to toggle the sheet's lock status.
Locking a worksheet prevents accidental modification of the data on
that worksheet.
. Click on the displayed icon to toggle the sheet's lock status.
Locking a worksheet prevents accidental modification of the data on
that worksheet.
The Viz column of the list shows an icon,
![]() , if the worksheet is currently visible. The Viz column
is blank if the worksheet is not visible.
Click in this column to toggle the worksheet's visibility.
When the visibility attribute is turned off, the worksheet does not get a
tab at the bottom of the Gnumeric window.
Its data is preserved, and references to cells on the non-visible
sheet continue to access the expected values.
Note that a non-visible worksheet cannot be selected from the list, although
the active fields in the list continue to function.
To apply functions that require selecting the worksheet, such as
Insert or Remove, first click in
the Viz column to make it visible.
, if the worksheet is currently visible. The Viz column
is blank if the worksheet is not visible.
Click in this column to toggle the worksheet's visibility.
When the visibility attribute is turned off, the worksheet does not get a
tab at the bottom of the Gnumeric window.
Its data is preserved, and references to cells on the non-visible
sheet continue to access the expected values.
Note that a non-visible worksheet cannot be selected from the list, although
the active fields in the list continue to function.
To apply functions that require selecting the worksheet, such as
Insert or Remove, first click in
the Viz column to make it visible.
The Dir column of the list shows a right-pointing or left-pointing arrow, depending on whether the sheet is currently set to be displayed left-to-right or right-to-left. Click on the arrow to toggle a worksheet's display direction.
The Rows and Cols columns show the current size of each worksheet. Worksheet size cannot be adjusted here.
To change the name of a worksheet, click in its New Name field until the contents of the field, if any, are highlighted, then type the desired new name and press Enter. If the new name duplicates a name already in use, a warning is displayed. You can change the new name or you can assign a new name to the other worksheet with that name. Name changes are not applied immediately. Instead, Gnumeric waits until you click on the Apply Name Changes button and makes all the name changes at once. When you apply the name changes, Gnumeric automatically updates all cell references that include worksheet names to use the new names.
The worksheets can be re-ordered in the workbook by pressing the left mouse button in a worksheet's line and dragging it up or down in the list of worksheets. You can also select a single worksheet and then click on the Up or Down button to move it up or down in the list. Alternatively, you can sort the worksheets into ascending or descending order by name by clicking on the Ascending or Descending button.
You can add an empty worksheet by clicking on Insert, to add the worksheet ahead of the selected worksheet, or on Append, to add the worksheet after the last sheet in the list. Insert creates a new worksheet the same size as the currently selected worksheet, while Append creates a new worksheet of the default size.
Click on Remove to delete the currently selected worksheet or worksheets.
Click on Duplicate to add an exact copy of the selected worksheet to the list immediately following the selected sheet. The name of the new worksheet is the same as the name of the duplicated worksheet, but with “(n)” appended, where n is the smallest integer greater than 1 that produces a unique worksheet name. If the worksheet name already ends in “(n)”, nothing is appended. Instead, the value of n is increased to the smallest value that produces a unique worksheet name.
To change the background color of the tabs for the selected worksheets,
click on the background color fill button,
 to set the background color to the color shown below the bucket icon, or
click on the downward-pointing arrow to access the color selection dialog.
to set the background color to the color shown below the bucket icon, or
click on the downward-pointing arrow to access the color selection dialog.
Similarly, to change the color of the text in the tabs of the selected worksheets,
click on the text color button,
 to set the text color to the color shown below the character icon, or
click on the downward-pointing arrow to access the color selection dialog.
to set the text color to the color shown below the character icon, or
click on the downward-pointing arrow to access the color selection dialog.
11.6.4. Adding a Blank Worksheet
A new, empty worksheet can be added to a workbook by insertion ahead of the worksheet currently displayed in the cell grid or by appending one after the last worksheet.
A new worksheet can be inserted ahead of the current worksheet by selecting from the menu or from the worksheet tab context menu or by using the Insert function of the Manage Sheets dialog described above. The new worksheet will be the same size as the one currently displayed.
A new worksheet can be added to the end of the list by selecting from the worksheet tab context menu or by using the Append function of the Manage Sheets dialog described above. The new worksheet will be the default size.
11.6.5. Copying or Pasting a Worksheet
Gnumeric does not directly support copying and pasting of worksheets, however copying blocks of cells provides a very similar function. For example, to replace the contents of worksheet Sheet3 with the contents of Sheet1, begin by selecting the worksheet tab for Sheet1. Select all the cells in Sheet1 by clicking on the blank rectangle at the top of the row headers, to the left of the column headers, or by selecting from the Edit menu. Next use or to copy the worksheet contents to the clipboard, depending on whether you want to copy or move the information. Select the worksheet tab for Sheet3 and select cell A1 or the entire worksheet, then use or from the Edit menu to copy the contents of Sheet1 into Sheet3.
Use of Paste Link in the Paste Special dialog should be avoided when operating on whole worksheets, as it creates links to every selected cell in the first worksheet, 16,777,216 cells in a worksheet of the default size, and has no option to skip empty cells in the first worksheet.
A similar operation can be performed using the Manage Sheets dialog. Duplicate the worksheet to be copied, then move the copy to precede or follow the worksheet it is to replace. Delete the second worksheet and rename the copy. This operation is similar to the copy and paste technique described above, but this method also copies metadata, such as the display appearance controlled by the submenu.
12. Workbook Settings
This chapter explains the contents of a Gnumeric workbook which are not part of the worksheets. This includes several settings which apply to the workbook and are saved in the Gnumeric file. Settings which apply to the Gnumeric program itself are called `preferences' and are explained in Chapter 13 ― Configuring Gnumeric.
- 12.1. Overview
- 12.2. Document Summary
- 12.3. Document Settings
- 12.4. Document Named Elements
12.1. Overview
The contents of a Gnumeric file describe all of the elements which can be changed by the user. This sections examines all of the workbook contents which are not part of the worksheets.
This chapter has not yet been written.
12.2. Document Summary
A small amount of metadata is associated with each document. These metadata describe the author of the document and other related information.
12.3. Document Settings
- 12.3.1. Document Printing Settings
- 12.3.2. Document Autosave Settings
- 12.3.3. Document Autocorrection Settings
- 12.3.4. Document View Settings
- 12.3.5. Document Protection Settings
- 12.3.6. Document Validation Settings
- 12.3.7. Document Recalculation Lag Settings
12.3.2. Document Autosave Settings
The AutoSave tool can save your workbook automatically at specific intervals. You can specify how often you want your work to be saved by entering a number in the ``Minutes'' box. If you check the ``Prompt before saving'' button on, Gnumeric asks a confirmation before each automatic save.
13. Configuring Gnumeric
This chapter explains how to change the default behaviour of Gnumeric including the startup behaviour and default locale (language and number display).
- 13.1. Overview
- 13.2. General Preferences
- 13.3. Toolbars
- 13.4. Plugins
- 13.5. Languages and Locales
13.1. Overview
Several preferences which relate to Gnumeric as a whole can be configured and will affect the appearance and behaviour of the program every time it is run. These preferences can be set by the user.
Gnumeric provides a main preference configuration panel which allows users to configure fundamental properties of the program including the font used within the spreadsheet, the type of file generated when a workbook is saved, default settings for the tools and the 'undo' mechanism, as well as several fundamental properties of the program, such as the pixel pitch of the display, which require advanced knowledge to understand. Section 13.2 ― General Preferences explains how to alter these preferences.
The toolbars can also be configured by being hidden from view. This allows Gnumeric to be fit into a smaller space. Section 13.3 ― Toolbars explains how to hide or show each toolbar.
Much of the functionality of Gnumeric is provided through the plugin mechanism. Individual plugins can be disabled to save memory space or when the plugin computer code is being altered. Section 13.4 ― Plugins explains how to disable and re-enable Gnumeric plugins.
Gnumeric is designed to be used around the globe and therefore allows the use to determine the language for the menus and to determine location specific information such as the character used to separate whole numbers from fractional units. These language and locale settings are explained in Section 13.5 ― Languages and Locales.
13.2. General Preferences
Gnumeric provides several general preferences which can be set by the user using the Preferences Dialog.
The Preferences Dialog has several pages. Each page addresses a certain aspects of using Gnumeric. The pages are selected by clicking on one of the options in the top left column. These act like a tab interface in changing the rest of the dialog options.
When the mouse pointer is placed over an entry field or a checkbox, after a certain delay, a temporary tooltip may appear. The tooltip is a small window with information about each option. The tooltip disappears once the mouse pointer is moved to a new area of the screen.
Certain of the options, such as the options for changing the number of pixels per length (the 'pixel pitch') on the screen, are generally set correctly automatically. These options are fundamental and should only be changed by users who understand the option.
- 13.2.1. Using the Preferences Dialog
- 13.2.2. Font Preferences
- 13.2.3. Copy and Paste Preferences
- 13.2.4. File Preferences
- 13.2.5. Tools Preferences
- 13.2.6. Undo History Preferences
- 13.2.7. Windows Preferences
13.2.1. Using the Preferences Dialog
The preference dialog can be started by selecting the and then the menu item.
The dialog is used by selecting one of the categories in the top left column of options and then changing the settings for that option. The categories are presented as a list; each can be selected in turn by placing the mouse pointer over the desired element and clicking with the primary mouse button.
Certain elements, such as the Font preference, have a small triangle in front of their name. Clicking on this triangle will open a sub-element line which allows the sub-element to be selected and have its options altered.
13.2.2. Font Preferences
The font preferences allow the user to change the font which is used by default in the Gnumeric grid cells and to set the font used for headers and footers when printing.
The Font selection sets the default font name, size and style to be used in the cells on every sheet.
The Headers/Footers selection sets the font name, size and style which will be used, by default, in the headers and footers added to each page of printed output. These selections can be over-ridden in the print preferences dialog as explained in Chapter 15 ― Printing. The content of the headers and footers is determined via the Page Setup dialog, detailed in Section 15.2 ― Page Setup..
13.2.3. Copy and Paste Preferences
The Copy and Paste element allows the user to determine how copied items are integrated into the clipboard mechanism.
13.2.4. File Preferences
The Files element provides settings related to the handling of files.
If you are usually using one of a small number of documents, you should set the Length of File History to be slightly larger than the number of these documents.
13.2.5. Tools Preferences
The Tools element allows to determine the settings for the recently used function list, for autocompletion of data entry in cells and for range selections.
The Sorting element allows to determine the default settings for the Sort Dialog.
13.2.6. Undo History Preferences
The Undo element permits to customize the undo feature. You would normally like the number of undo items to be in the 10 to 25 range and the maximal undo size to be 10000 to 100000, unless you only have little memory available.
13.2.7. Windows Preferences
The windows preferences include options to set the default appearance of the whole window displaying the Gnumeric interface as well as
The Windows element includes a variety of options that did not fit within any of the other tabs.
The Screen elements allows the user to set the pixel pitch (number of pixels per length) for the screen. This is a fundamental property of the display which should be set correctly by default.
These options affect the display of Gnumeric and should only be changed after serious consideration. By default these options should be correct and should only be altered for non-standard screens and when the appearance of Gnumeric and its contents are clearly incorrect.
13.3. Toolbars
The three Gnumeric toolbars can either be hidden from view or shown above or below the cell grid area. The three different toolbars are explained in Section 4.4 ― Toolbars.
Toolbars can be hidden or shown by clicking with the primary mouse button on the menu, the dragging the pointer down to the to open its submenu and then moving the pointer into the sub-menu listing the three toolbars. By default each toolbar appears with a small check mark in front of its name indicating that it is visible. Clicking on any of the toolbars will alter its setting, making the toolbar visible if it is hidden or hiding the toolbar if it is visible.
13.4. Plugins
Gnumeric allows users to configure the plugins which are currently in use. The Plugin Manager provides all the configuration options in one location.
The Plugin Manager can be started by clicking on the menu and selecting the menu item.
The Plugin Manager is a tabbed dialog with three tabs. The first tab, labeled Plugin List, provides a list of all the currently visible plugins, the second tab, labeled Plugin Details provides details on the plugin selected in the first tab. The third tab, labeled Directories lists the directories which are currently searched to discover new plugins.
The first tab provides a list of plugins, an explanation of each and a method to activate or de-activate the plugin. The list includes all of the plugins which have been found by Gnumeric in the directories listed in the third tab. An explanation can be obtained for each plugin by selecting the plugin from the list by placing the mouse pointer over the plugin name and clicking with the primary mouse button. The explanation will then appear in the bottom text area. The active column provides check boxes in front of each listed plugin. If the box contains a check mark, the plugin has been activated and its functionality should be available.
13.5. Languages and Locales
Gnumeric can be run in many languages with settings for number formats, currencies and dates appropriate to each particular area. Unfortunately, this aspect of the program is exceedingly complex and requires the proper participation of the underlying operating system. This dependency makes it impossible for this manual to provide a complete explanation. The operating system should include a complete discussion of locales and location settings.
By default, Gnumeric finds the configuration currently used by the user and sets the language and locale settings appropriately.
It is also possible to run Gnumeric using the language and locale settings for a different place. This should be possible simply by redefining the LC_ALL environmental variable. For example, using the bash shell it should be possible, within a terminal, type:
LC_ALL=fr_FR gnumeric &
14. Working with Files
This chapter explains how to use files in Gnumeric. The chapter provides an extensive description of the file formats used by Gnumeric. The chapter also explains how to open files, import data from text files, save files, export data to text files, send data to others via electronic mail, and convert files from one format to another.
- 14.1. Files in Gnumeric
- 14.2. File Formats
- 14.3. Opening Files
- 14.4. Importing Text Files
- 14.5. Saving Files
- 14.6. Exporting Text Files
- 14.7. Sending Files
- 14.8. Converting Files
14.1. Files in Gnumeric
Gnumeric stores its information by creating files and re-opening these files during a future session. Saving information to files also allows a user to send the information to others.
The default file format for Gnumeric is based on the eXtensible Markup Language (XML). By default, files are saved as text files, consisting of XML, which are then compressed using the library of the gzip program. The extension for Gnumeric files is .gnumeric on platforms which support file extensions of any size, .gnum for systems which restrict extensions to four letters, or .gnm for systems which restrict extensions to three letters.
Gnumeric can also open or save files in a number of other file formats. The project prides itself for the work reverse engineering and supporting the file formats used by Microsoft Excel. Gnumeric can use the Excel file format as if it were the native file format, meaning that Gnumeric can store and retrieve essentially every aspect of a worksheet using the Excel format. Similarly, Gnumeric supports the OASIS Open Document Format for Office Applications (ODF 1.2) file format (ISO/IEC 26300:2006/Amd 1:2012) as well as the ECMA 376 2nd Edition file format (ISO/IEC 29500:2008) as if they were the native format.
Gnumeric cannot delete files from the file system. Gnumeric can open existing files and create new files but cannot delete files once they are created. Files can be deleted using a file browser such as Nautilus on the GNOME desktop or using the command-line program rm.
This chapter discusses working with actual files. It is also possible to import data into Gnumeric using the clipboard by copying either text or html table information in another program and then pasting the resulting data into a worksheet. See Section 5.7.4 ― Cut and Paste Between Gnumeric and Other Applications for details.
Text files are often used to store data, using many different systems to structure the data such as using commas, tabs or spaces to separate values. Gnumeric features a flexible system that enables users to define exactly the structure of the text file to be imported or exported.
Gnumeric can be integrated with an email client to allow files to be sent directly as attachments to an electronic mail message.
Gnumeric also features a command-line tool called ssconvert to convert files between any of the file formats which it supports.
14.2. File Formats
Gnumeric supports numerous file formats in addition to its own XML based format. The table below lists the formats currently supported. In the table below, the name of the format is a link which can be used to jump to the section which discusses the format.
| Format | Extension | Open | Save | Import | Export | MIME type |
|---|---|---|---|---|---|---|
| Gnumeric | .gnumeric / .gnm / .xml | YES | YES | application/x-gnumeric | ||
| Applix | .as | YES | application/x-applix-spreadsheet | |||
| Comma/Tab/Semicolon Separated Values | .csv/.tsv | YES | YES | text/plain | ||
| Data Interchange Format | .dif | YES | YES | |||
| GNU Oleo | .oleo | YES | application/x-oleo | |||
| HTML | .html / .htm | YES | YES | text/html | ||
| LaTeX | .tex | YES | text/x-tex | |||
| Linear and Integer Program | none / .mps | YES | application/x-mps | |||
| Lotus 1-2-3 | .wk1 / .wks | YES | application/vnd.lotus-1-2-3, application/x-123 | |||
| Microsoft Excel Old Binary Format (versions 2 - 5) | .xls / .xlt / .xlw | YES | application/vnd.ms-excel | |||
| Microsoft Excel Binary Format (Excel 95 - 2003) | .xls / .xlt / .xlw | YES | YES | application/vnd.ms-excel | ||
| Microsoft Excel 2003 SpreadsheetML | .xlsx | YES | application/vnd.ms-excel | |||
| Microsoft Office Open SpreadsheetML (MOOX/ECMA376/ISO29500) | .xlsx | YES | YES | application/vnd.ms-excel | ||
| OpenOffice.Org / StarOffice Old Format | .sxc / .stc | YES | application/vnd.sun.xml.calc | |||
| OpenDocument Format (OASIS ODF and ISO/IEC 26300:2006) | .ods / .odt / .sxc / .stc | YES | YES | application/vnd.oasis.opendocument.spreadsheet | ||
| Paradox Database | .px / .db | YES | YES | |||
| Plan Perfect | .pln | YES | application/x-planperfect | |||
| Psion 5 Sheet Files | .psisheet | YES | ||||
| PostScript | .ps / .eps | YES | application/postscript | |||
| YES | application/pdf | |||||
| Quattro Pro | .wb1 / .wb2 / .wb3 | YES | application/x-quattropro, application/x-quattro-pro | |||
| SC/XSpread | none / .sc | YES | application/x-sc | |||
| Multiplan (SYLK) | .sylk / .slk | YES | YES | application/x-sylk | ||
| Text Formats | .txt / .text | YES | YES | text/plain | ||
| TROFF | .me | YES | application/x-troff | |||
| Xbase | .dbf | YES | application/dbase, application/dbf, application/x-dbase, application/x-dbf, application/x-xbase, zz-application/zz-winassoc-dbf | |||
| XHTML | .xhtml / .html | YES | application/xhtml+xml |
Files in the file formats marked as Save/Open can be opened or saved with the , , and menu items in the menu. Files in the file formats marked as Import/Export can be imported or exported with the items on the and submenus of the menu.
- 14.2.1. Gnumeric XML File Format
- 14.2.2. Applix File Format
- 14.2.3. Comma/Tab/Semicolon Separated Value (CSV/TSV) File Formats
- 14.2.4. Data Interchange Format (DIF) File Format
- 14.2.5. GNU Oleo File Format
- 14.2.6. The HTML File Format
- 14.2.7. LaTeX File Format
- 14.2.8. Linear and Integer Program Expression (MPS) File Format
- 14.2.9. Lotus 1-2-3 File Format
- 14.2.10. Microsoft Excel Old Binary File Format
- 14.2.11. Microsoft Excel New Binary File Format
- 14.2.12. Microsoft Excel 2003 XML File Format
- 14.2.13. Microsoft Excel Office Open XML SpreadsheetML
- 14.2.14. Microsoft Excel XML
- 14.2.15. Multiplan SYLK File Format
- 14.2.16. OpenDocument Format (OASIS ODF and ISO/IEC 26300:2006)
- 14.2.17. OpenOffice.org Old File Format
- 14.2.18. Plan Perfect File Format
- 14.2.19. PostScript File Format
- 14.2.20. Portable Document Format (PDF) File Format
- 14.2.21. Quattro Pro File Format
- 14.2.22. SC/Xspread File Format
- 14.2.23. Text File Formats
- 14.2.24. TROFF File Format
- 14.2.25. Xbase File Format
- 14.2.26. XHTML File Format
14.2.1. Gnumeric XML File Format
The Gnumeric file format is based on the eXtensible Markup Language (XML) and is used as the default file format.
Gnumeric is currently using two different systems to process XML.
The newer system is based on the SAX processing method for XML and is substantially faster than the older method. This code is based in a plugin module. The exporter is currently used by default but the importer is still incomplete.
The older system is part of the core Gnumeric program and is still used to open files in the Gnumeric format.
| Name: | The Gnumeric file format |
| Extensions: | .gnumeric |
| Compatible Programs: | Gnumeric |
| Open / Save: | Both |
- Limitations
-
This is the default file format and therefore has the best support of all the formats available. Every feature that can be created in the spreadsheet should be savable using this format.
- Plugin
-
The Gnumeric file format is handled using two different code bases. The older version is part of the application itself. The newer version is in a plugin called "EXPERIMENTAL SAX based XML" because the parser is based on SAX.
- Format Details
-
The Gnumeric file format stores the file contents in the eXtensible Markup Language (XML) and compresses the file using the GNU project's gzip compression library.
The Gnumeric file format is designed to be flexible and powerful. The format is easily processed by computers. The format can readily be improved as gnumeric develops without breaking compatibility with older versions. The format is designed to be easily translated into text so that it can be read by humans.
Gnumeric automatically recognizes the version of the file format of any file saved since this format is contained in the file header. The table below is for information purposes only.
Table 14-2 Gnumeric XML format versionsXML File Format Version Gnumeric Version 1 2 3 Since 0.52 4 Since 0.57 5 Since 0.58 6 Since 0.62 7 Since 0.66 8 Since 0.71 9 Since 0.73 10 Since 1.03 An outdated PDF document discussing the Gnumeric file format which should provide a useful starting point was developed by the JWorkbook project. The file can be downloaded from http://www.jfree.org/jworkbook/download/gnumeric-xml.pdf.
- Further Processing
-
Direct manipulation of Gnumeric files is possible by transforming the files to text files and then using standard text file tools like document editors. In order to read the contents a Gnumeric file must first be decompressed and can then be opened. In GNU systems, the Gnumeric default file "Book1.gnumeric" can be uncompressed as follows:
alternatively, the file can be renamed and then uncompressed with the following pair of commands:zcat Book1.gnumeric > Book1.text
both possibilities yield the file "Book1.text" which is an ASCII text file. This file can be opened in any editor, like Vim or Emacs, or pager, like Less.cp Book1.gnumeric Book1.text.gz gunzip Book1.text.gz
XML manipulation tools can be used to transform Gnumeric files and access the data they contain, since the file format is XML. The file can be validated by an XML Schema Definition (XSD) . These are available via the Internet at http://git.gnome.org/cgit/gnumeric/plain/gnumeric.xsd.
The Java™ Language can be used to create, access, or manipulate Gnumeric format files using the JWorkbook project library. See the project's website for details.
The C# language, through the mono implementation can also be used to manipulate Gnumeric format files.
14.2.2. Applix File Format
The Applix file format is used by the Applixware group of applications which include a spreadsheet component. The Applixware spreadsheet is made by Vistasource and claims to be a 'real-time', event driven software system.
Gnumeric can read some files produced by the Applixware spreadsheet.
| Name: | The Applix File Format |
| Extensions: | .as |
| Compatible Programs: | The Applixware Spreadsheet |
| Import / Export: | Import only |
- Limitations
-
Saving Applixware files has recently been disabled due to lack of developer interest. Instead of directly saving a file in the Applix format, files can be exported to Applixware can be performed using the Excel file format.
- Plugin
-
Supported by the Applix plugin.
- Format Details
-
14.2.3. Comma/Tab/Semicolon Separated Value (CSV/TSV) File Formats
The Comma Separated Value (CSV) and Tab Separated Value (TSV) file formats are a common structuring strategy for text format files. In these files, each line in the file represents a row of data and, within each line of the file, the different data fields are separated from one another using a separator character, often a comma, semicolon or tab. Gnumeric handles CSV and TSV files through the text importer and exporter but these formats are given their own definitions in this document because they are considered very common formats.
Gnumeric will automatically open CSV and TSV format files separating each row into columns based on the presence of appropriate separator characters in the file. If the automatic import leads to any errors, these can generally be corrected by using the "Text Import (configurable)" file format instead. Selecting that file format will launch the Text Import druid which allows the user to import CSV and TSV format files while specifying in greater detail the settings of the import configuration parameters. See the section on importing text files or the section on exporting text files for an explanation of how to open or save CSV and TSV files through the Text Import druid.
| Name: | Comma/Semicolon/Tab Separated Value, CSV/TSV |
| Extensions: | .csv, .tsv, .txt |
| Compatible Programs: | Many |
| Import / Export: | Both |
- Limitations
-
The CSV file format is only useful for the exchange of cell data and cannot be used for sheet objects like graphical plots. This file format cannot save the formatting of cell contents, backgrounds or borders.
- Plugin
-
Supported by the core Gnumeric program.
- Format Details
-
CSV files are simple text files where each row of the text file represents one row in the spreadsheet and where the cells within a row are separated from each other by a comma.
- Further Processing
-
CSV files can be processed using any tool which operates on text files. The CSV format is also common as a format which can be opened by applications.
See the section on Text Formats
14.2.4. Data Interchange Format (DIF) File Format
The Data Interchange Format (DIF) file format is a text based format encoded in ASCII with a header, for integrity checking, and a body. The format was originally developed by Software Arts in order to transfer data from VisiCalc, the first spreadsheet.
| Name: | Data Interchange Format |
| Extensions: | .dif |
| Compatible Programs: | Various |
| Import / Export: | Both |
- Limitations
-
Since the DIF format only supports a single worksheet, Gnumeric only exports the top worksheet in the view used to save the workbook.
- Plugin
-
Supported by the “Data Interchange Format (DIF) module” plug-in.
- Format Details
-
The format is a text file, encoded in ASCII, with a header and body.
- Further Processing
-
The file can be processed as a text file or imported to any program that recognizes the DIF format.
14.2.5. GNU Oleo File Format
The GNU Oleo file format is the format used by the GNU Oleo spreadsheet, one of the early free software spreadsheets. The GNU Oleo project has stagnated so this format is only supported to enable the import of old files.
| Name: | GNU Oleo |
| Extensions: | Unknown |
| Compatible Programs: | GNU oleo |
| Import / Export: | Open Only |
- Limitations
-
- Plugin
-
Supported by the 'GNU Oleo' plugin.
- Format Details
-
14.2.6. The HTML File Format
The Hypertext Markup Language (HTML) file format is a text file format with markup in the Hypertext Markup Language. These files are designed to be viewed in a web browser.
Gnumeric can save the cell contents in a worksheet to a text file which consists either of entire, well formed HTML files of version 3.2 or 4.0, or of a file fragment which contains only a <table> structure and must be inserted into an HTML file. Gnumeric can also open files which consist only of simple, well formed HTML <table> structures.
| Names: | Hypertext Markup Language (HTML) |
| Extensions: | .html, .htm |
| Compatible Programs: | Any Web Browser, any text editor |
| Import / Export: | Export only, but also can import HTML <table> structures |
- Limitations
-
Only the cell contents of a worksheet are saved with sheet object elements, such as graphical plots, ignored.
- Plugin
-
Supported by the 'HTML & TeX' plugin.
- Further Processing
-
All these files can be opened by any text editor. The HTML 3.2 and 4.0 format files can be opened by any web browser such as Mozilla.
Files which are generated as HTML fragments must be placed into an HTML file with a valid pre-amble and closing statements.
See Also: XHTML Format
14.2.7. LaTeX File Format
The LaTeX file format is a text file format with markup in the LaTeX 2ε derivative of the TeX family of languages.
Gnumeric generates LaTeX files to allow the export of tables of numeric values for use in the LaTeX document processing system. LaTeX is a derived format of the TeX system. The files generated by Gnumeric are designed to be used by a LaTeX processor, such as latex or pdflatex, to generate files in viewable formats such as Device Independent (DVI), PostScript (PS) or Portable Document Format (PDF).
The generated files can either be processed directly or can be included in other LaTeX files.
| Name: | LaTeX |
| Extensions: | .tex |
| Compatible Programs: | latex, pdflatex |
| Import / Export: | Export only |
- Limitations
-
Gnumeric generates a LaTeX longtable structure which contains only the contents of the cells in the worksheet displayed in the view at the time the file was created.
Font coloring is supported. Thin cell borders are translated into single lines and thick cell borders are translated into double lines. Cell background colors are ignored.
- Plugin
-
Supported by the 'HTML & TeX' plugin.
- Format Details
-
The generated file includes extensive documentation in TeX comment fields, to explain how to use and alter the file. Lines in the file which are comments begin and end with double percent symbols (%%). Lines which are designed as user options begin with a single percent symbol (%) which can be deleted to make the LaTeX command on that line take effect.
- Further Processing
-
The LaTeX files generated by Gnumeric can either be processed directly by a LaTeX processor or can be included as tables in other files. The files can be included by reference as explained below or can be pasted into other files at the appropriate location. The file can also be altered to change certain parameters. These alterations are explained as comments within the file itself and are presented below.
The file created by Gnumeric can be run directly through a LaTeX processor without any modifications. For example, if the file were saved as Book1.tex, the following command
generates a PDF file named Book1.pdf. The file can be generated in landscape format and the headers, footers and column widths of the file can be altered in the manner explained below.pdflatex Book1.tex
The file can also be included within another LaTeX file to provide a single table. This requires, first, ensuring that all the packages which will be needed are included, and second, defining a LaTeX variable which is used as a dummy tag to exclude the preamble used to process the file on its own. The LaTeX file generated by Gnumeric requires using the following lines in the preamble
to include each of these packages. Optionally, to include the table in landscape mode, the preamble also needs the line\usepackage{ucs} \usepackage{utf8}{inputenc} \usepackage{color} \usepackage{array} \usepackage{longtable} \usepackage{calc} \usepackage{multirow} \usepackage{hhline} \usepackage{ifthen}to include the lscape package. Second, the following line\usepackage{lscape}must be included to make the LaTeX processor ignore the preamble section of the file generated by Gnumeric. The generated file can be included either by adding, at the appropriate location in the other file, the line\def\inputGnumericTable{}with the text mygnumericfile replaced with the appropriate file name or by pasting the entire file generated by Gnumeric into the other file.\input{mygnumericfile.tex}An option is provided in the file allows the table to be presented in landscape mode which allows wider tables to be included. For files which are to be processed independently, the option can be changed in the document class definition
by removing the percent symbol (%) in front of ,landscape. For files to be included as tables in other LaTeX files, the preamble must include the lscape package, as was explained above, and the two commands\documentclass[12pt% %,landscape% ]{report}must have the leading percent sign removed.\def\gnumericTableEnd{\end{landscape}} \begin{landscape}An option is provided to change the widths of the columns of the file generated by Gnumeric. By default, the file attempts to maintain the proportions between the columns in the Gnumeric worksheet, yet scale the resulting table for the width of the paper defined in LaTeX. To change the column widths, look for the section in the LaTeX file with lines that look like
and that may have as many entries as there were columns in the worksheet. The TeX 'lengths' defined for each column can be changed. For example, change the second column (Column B) to a width of 0.75 inches, we would simply have to modify this code to:\def\gnumericColA{107pt*\gnumericScale} \def\gnumericColB{89pt*\gnumericScale} \def\gnumericColC{98pt*\gnumericScale} \def\gnumericColD{89pt*\gnumericScale} \def\gnumericColE{89pt*\gnumericScale}and the resulting file would have a second column 0.75 inches wide.\def\gnumericColA{107pt*\gnumericScale} \def\gnumericColB{0.75in} \def\gnumericColC{98pt*\gnumericScale} \def\gnumericColD{89pt*\gnumericScale} \def\gnumericColE{89pt*\gnumericScale}An option to change the headers and footers of the table is provided as well. The file itself contains comments on how to alter these but the choices will require seeing the documentation of the longtable LaTeX package. See that documentation and the contents of the file generated by Gnumeric for details.
14.2.8. Linear and Integer Program Expression (MPS) File Format
The Linear and Integer Program Expression file format is a text file format, encoded as ASCII, which uses fixed columns. The format was developed by International Business Machines Corporation to express linear and integer programs.
| Name: | Linear and Integer Program Expression (MPS) |
| Extensions: | none / .mps |
| Compatible Programs: | Various linear programming applications |
| Import / Export: | Import only |
- Limitations
-
- Plugin
-
Supported by the 'Linear and integer expression (MPS) format module' plug-in.
- Format Details
-
The Argonne National Laboratory of the United States has a simple introduction to the MPS format on their web site.
The MIPLIB site has more information including a file named mps_format which is a brief introduction to the format and includes the following section:
and provides further explanations to the components. The file also suggests as more complete references:The following template is a guide for the use of MPS format: --------------------------------------------------------------------- Field: 1 2 3 4 5 6 Columns: 2-3 5-12 15-22 25-36 40-47 50-61 NAME problem name ROWS type name COLUMNS column row value row value name name name RHS rhs row value row value name name name RANGES range row value row value name name name BOUNDS type bound column value name name ENDATA ---------------------------------------------------------------------which should provide a better explanation."Advanced Linear Programming," by Bruce A. Murtagh "Computer Solutions of Linear Programs," by J.L. Nazareth
14.2.9. Lotus 1-2-3 File Format
The Lotus 1-2-3 file format is the format used by the Lotus 1-2-3 spreadsheet, which is now part of the office suite called SmartSuite.
| Name: | Lotus 1-2-3 |
| Extensions: | .wk1,.wks |
| Compatible Programs: | Lotus SmartSuite |
| Import / Export: | Import only |
- Limitations
-
- Plugin
-
Supported by the 'Lotus 123' plugin.
- Format Details
-
- Further Processing
-
Many spreadsheet programs support this format.
14.2.10. Microsoft Excel Old Binary File Format
The Microsoft Excel™ Old Binary file format is a binary file format used by the Excel program in the Office suite between versions 2 and 5. The format is a common format supported to various extents by most spreadsheets although it is incompletely documented. The Gnumeric project has reversed engineered all of the core features of the format.
| Name: | Excel |
| Extensions: | .xls |
| Compatible Programs: | Microsoft Excel, Microsoft Office, and many other spreadsheets |
| Open / Save: | Both |
- Plugin
-
Supported by the 'MS Excel (tm)' plugin.
- Format Details
-
These are binary file formats.
- Further Processing
-
A number of other programs are able to process files in the Microsoft Excel file format.
14.2.11. Microsoft Excel New Binary File Format
The Microsoft Excel™ New Binary file format is a binary file format used by the Excel program in the Office suite between versions 95 and 2003. The format is a common format supported to various extents by most spreadsheets although it is incompletely documented. The Gnumeric project has reversed engineered all of the core features of the format.
| Name: | Excel |
| Extensions: | .xls |
| Compatible Programs: | Microsoft Excel, Microsoft Office, and many other spreadsheets |
| Open / Save: | Both |
- Plugin
-
Supported by the 'MS Excel (tm)' plugin.
- Format Details
-
These are binary file formats.
- Further Processing
-
A number of other programs are able to process files in the Microsoft Excel file format.
14.2.12. Microsoft Excel 2003 XML File Format
Microsoft Excel™ 2003 shipped with a file format called SpreadsheetML. This file is XML. It is not very common, but its core features are supported.
| Name: | Excel |
| Extensions: | .xlsx |
| Compatible Programs: | Microsoft Excel, Microsoft Office, and many other spreadsheets |
| Open / Save: | Both |
- Plugin
-
Supported by the 'MS Excel (tm)' plugin.
- Format Details
-
These are zip files containing SpreadsheetML files and binary files.
- Further Processing
-
This file format is not very widespread and therefore support by 3rd-party applications is limited.
14.2.13. Microsoft Excel Office Open XML SpreadsheetML
Microsoft Office™ 2007 shipped with a new set of file formats, namely the Microsoft Office Open XML SpreadsheetML format. This format is a semi-open standard based around a zipped XML file. Microsoft Office Open XML SpreadsheetML is mostly standardized in ECMA 376 and ISO 29500. This implementation is covered under the Open Specification Promise and therefore does not infringe upon Microsoft patents.
| Name: | Excel |
| Extensions: | .xls |
| Compatible Programs: | Microsoft Excel, Microsoft Office, and many other spreadsheets |
| Open / Save: | Both |
- Limitations
-
Most core features of the format are supported.
- Plugin
-
Supported by the 'MS Excel (tm)' plugin.
- Format Details
-
These are zip files containing SpreadsheetML files and binary files.
- Further Processing
-
A number of other programs are able to process files in the Microsoft Excel file format.
14.2.14. Microsoft Excel XML
The Microsoft Excel™ file format is a binary file format used by the Excel program in the Office suite. The format is a common format supported to various extents by most spreadsheets although it is incompletely documented. The Gnumeric project has reversed engineered all of the core features of the format.
| Name: | Excel |
| Extensions: | .xls |
| Compatible Programs: | Microsoft Excel, Microsoft Office, and many other spreadsheets |
| Open / Save: | Both |
- Limitations
-
Most core features of the format are supported.
Gnumeric does not support the very old file formats used by Excel™ versions prior to Excel™ 2.0.
Gnumeric can open files from most of the Microsoft Excel™ file formats and all of the recent file formats. The formats supported are:
- MS Excel™ 5.0/95.
- MS Excel™ 97/2000/XP.
- MS Excel™ 97/2000/XP & 5.0/95.
- Plugin
-
Supported by the 'MS Excel (tm)' plugin.
- Format Details
-
These are binary file formats.
- Further Processing
-
A number of other programs are able to process files in the Microsoft Excel file format.
14.2.15. Multiplan SYLK File Format
The Microsoft Multiplan Symbolic Link Interchange (SYLK) file format is a column based format.
Gnumeric can read files in this format.
| Name: | Symbolic Link Interchange (SYLK) |
| Extensions: | none / .slk |
| Compatible Programs: | Multiplan |
| Import / Export: | Import only |
- Limitations
-
- Plugin
-
Supported by the 'Multiplan (SYLK)' plugin.
- Format Details
-
14.2.16. OpenDocument Format (OASIS ODF and ISO/IEC 26300:2006)
The OpenOffice.org XML file format is zip archive including several components all of which are text files, most of these with markup in the eXtensible Markup Language (XML).
Gnumeric reads version 1.0, 1.1 and 1.2 of ODF spreadsheet files and writes version 1.2 files with or without foreign elements. Foreign elements are an extension mechanism defined in ODF and allow features to be saved in ODF files that are not specifically standardized by ODF. Gnumeric plans to continue to support this format in the future.
| Name: | Open Document Format, ODF |
| Extensions: | .ods |
| Compatible Programs: | OpenOffice.org Calc, LibreOffice Calc, KSpread, StarCalc |
| Open / Save: | Both |
- Limitations
-
- Plugin
-
Supported by the 'Open Document Format' plugin.
- Format Details
-
The file format is a zip archive containing several text and XML elements: a mimetype file giving the mime type, a content.xml file with the contents of the spreadsheet cells, and several other files with meta data, style definitions or information on the settings. The file contents can be extracted with the unzip command line program or with any of a number of graphical interface programs.
The Organization for the Advancement of Structured Information Standards (OASIS) has accepted this file format as the standard "OASIS Open Office XML Format". The published specification for the file format is available from the OASIS Open Office XML Format Technical Committee web page. Other information is available from the OpenOffice.org XML File Format web page, part of the OpenOffice.org project.
Version 1.0 of ODF was adopted as an international standard by ISO/IEC as ISO/IEC 26300:2006.
- Further Processing
-
Files in this format can be imported and modified by many different programs including the OpenOffice.org Calc and LibreOffice Calc spreadsheets or may be modified through XML processing.
14.2.17. OpenOffice.org Old File Format
OpenOffice.org originally shipped with a file format that has served as a basis for the new OASIS-standardized file format. This file format is deprecated.
Gnumeric can both open and save files in this format and plans to continue to support this format in the future.
| Name: | OpenOffice.org/StarOffice file format |
| Extensions: | .sxw |
| Compatible Programs: | OpenOffice.org Calc, StarCalc |
| Import / Export: | Both |
- Limitations
-
- Plugin
-
Supported by the 'Open Document Format' plugin.
- Further Processing
-
This file format is deprecated and is not widely used.
14.2.18. Plan Perfect File Format
The Plan Perfect file format is a format used by the PlanPerfect spreadsheet.
| Name: | Plan Perfect |
| Extensions: | Unknown |
| Compatible Programs: | PlanPerfect. |
| Import / Export: | Import only |
- Limitations
-
- Plugin
-
Supported by the 'Plan Perfect' plug-in.
- Format Details
-
- Further Processing
-
14.2.19. PostScript File Format
The PostScript file format is a text format which contains the program code for a postScript interpreter. PostScript is a page description language designed to enable the creation and transfer of printer-ready output.
Gnumeric supports the creation of PostScript files through the printing interface, not through the file save mechanism. See Chapter 15 ― Printing, for details on how to generate a PostScript file.
| Name: | PostScript |
| Extensions: | .ps |
| Compatible Programs: | Many programs can interpret and display PostScript files including: GGV, ghostview (gv), and ghostscript. |
| Import / Export: | Export only |
- Limitations
-
- Plugin
-
The creation of PostScript files is supported internally by the printing sub-system.
- Format Details
-
The PostScript language was created by Adobe, Inc. The Adobe web site has a non-technical introduction, as well as a technical overview and the actual specifications.
- Further Processing
-
PostScript files can imported into other documents by several programs. For the very advanced, PostScript files can be reprogrammed using a text editor.
14.2.20. Portable Document Format (PDF) File Format
The Portable Document Format (PDF) file format is a binary format which contains page description primitives and combines a subset of the Postscript language with some more recent features. The Portable Document Format is a page description language designed to enable the creation and transfer of printer-ready output.
Gnumeric supports the creation of PDF files through the printing interface, not through the file save mechanism. See Chapter 15 ― Printing, for details on how to generate a PDF file.
| Name: | Portable Document Format (PDF) |
| Extensions: | |
| Compatible Programs: | PDF is supported by a wide variety of programs including gPDF, Xpdf, GGV, ghostview (gv), and ghostscript, |
| Import / Export: | Export only |
- Limitations
-
- Plugin
-
The creation of PDF files is supported internally by the printing sub-system.
- Format Details
-
The Postscript language was created by Adobe, Inc. The Adobe web site has a non-technical introduction, as well as a technical overview and the actual specifications.
- Further Processing
-
PDF files can imported into other documents by several programs.
14.2.21. Quattro Pro File Format
The Quattro Pro file format is the format used by Corel's QuattroPro spreadsheet.
Gnumeric supports opening these files to import their data.
| Name: | Quattro Pro |
| Extensions: | .wb1 / .wb2 / .wb3 |
| Compatible Programs: | Quattro Pro |
| Import / Export: | Import only |
- Limitations
-
- Plugin
-
Supported by the Quattro™ Pro plugin.
- Format Details
-
14.2.22. SC/Xspread File Format
The SC/Xspread file format is the file format used by the old sc and Xspread spreadsheets.
| Name: | SC file format |
| Extensions: | YES |
| Compatible Programs: | SC, Xspread, S spreadsheets. |
| Import / Export: | Import only |
- Limitations
-
- Plugin
-
Supported by the 'SC/XSpread' plug-in.
- Format Details
-
14.2.23. Text File Formats
Files in the text file format are files in which the bytes represent the text characters of a particular character set using a specific system to relate the binary numbers in the file to the text characters of the set. Such systems are called 'encodings' and become an issue when the file includes characters that are not in the standard ASCII set, such as characters in languages other than English. Character encodings are explained in greater detail in Section 14.4.1.1 ― Character Encodings.
Choosing menu item in the submenu of the menu or the menu item in the submenu of the menu and specifying the "Text import (configurable)" or "Text export (configurable)" file formats to open or save files will cause Gnumeric to start the Text Import or Text Export druids. These allow the users to configure in detail the parameters with which existing files will be read into a workbook or existing workbooks will be output to a file.
The Text file format includes a number of different formatting strategies for text files in which data fields are structured in a regular pattern. Most of these formats represent rows of data on different lines of the file using different strategies to separated data values within each row. 'Fixed-width' formats place each data entry in a separate column and therefore limit the size of the data entries. 'Separated' formats use a special character or character sequence to separate entries. For instance, the comma separated value, the tab separated value formats and the space separated value formats use commas, tabs, and spaces respectively to separate the data fields.
Gnumeric can import and export files from and to a wide variety of text file formats when the text importer or the text exporter is configured appropriately. File can be generated with many different encodings. See the section on importing text files or the section on exporting text files for an explanation of how to import or export these formatted text files.
| Name: | Text File Format |
| Extensions: | .text / .txt / none |
| Compatible Programs: | Many programs can read and create formatted text files |
| Import / Export: | Both |
- Limitations
-
The exporter can only create text files using a separator character and cannot create fixed-width structured files.
- Plugin
-
Supported by the core Gnumeric program.
- Format Details
-
Text file format files are simple text files containing the data for each cell of the worksheet organized in a systematic fashion.
- Further Processing
-
Text format files can be processed using any tool which operates on text files, and many other applications can read or generate one or more of these formats.
14.2.24. TROFF File Format
The TROFF file format is a text file format with markup in TROFF.
The TROFF system is a documentation preparation system that can generate many different output files from an input file with standard markup. Gnumeric produces a file that can be used as input to the TROFF system or its GNU project replacement, GROFF.
The support for this format is mostly intended to produce simple tables into a file which can be used in the TROFF system. Since Gnumeric supports full output to Postscript and PDF file formats, those formats should be used to generate graphics for plots and drawing elements.
| Name: | TROFF |
| Extensions: | .me |
| Compatible Programs: | TROFF, GROFF |
| Import / Export: | Export only |
- Limitations
-
- Plugin
-
Supported by the 'HTML & TeX' plugin.
- Format Details
-
- Further Processing
-
Two examples of the TROFF system will illustrate how to use this file format. Both examples start with a simple worksheet which consists of a simple grid of cells with cell contents, which has been used to create a file called "myfile.me" in the TROFF file format.
A table in PostScript file format can be created starting from the file generated by Gnumeric. The command
will create a PostScript file of the corresponding table. Note, however, that Gnumeric itself can make a Postscript file of the table directly through the printing system.groff -me -t -Tps myfile.memyfile.ps
A table in PostScript file format can be created starting from the file generated by Gnumeric. The command
creates an ascii (straight text) file. This file will look like:groff -me -t -Tascii myfile.memyfile.ascii
Sheet 0 +----------+------------------+-------------+------------+---+ | | Operating System | | | | +----------+------------------+-------------+------------+---+ | | DOS | Linux | SCO | | +----------+------------------+-------------+------------+---+ | January | $1000.00 | $900.00 | $500.00 | | +----------+------------------+-------------+------------+---+ | February | $900.00 | $2500.00 | $300.00 | | +----------+------------------+-------------+------------+---+ | March | $800.00 | $4100.00 | $100.00 | | +----------+------------------+-------------+------------+---+ | April | $700.00 | $5700.00 | ($100.00) | | +----------+------------------+-------------+------------+---+ | May | $600.00 | $7300.00 | ($300.00) | | +----------+------------------+-------------+------------+---+ | June | $500.00 | $8900.00 | ($500.00) | | +----------+------------------+-------------+------------+---+ | July | $400.00 | $10500.00 | ($700.00) | | +----------+------------------+-------------+------------+---+ | August | $300.00 | $12100.00 | ($900.00) | | +----------+------------------+-------------+------------+---+ |September | $200.00 | $13700.00 | ($1100.00) | | +----------+------------------+-------------+------------+---+ | October | $100.00 | $15300.00 | ($1300.00) | | +----------+------------------+-------------+------------+---+ | November | $0.00 | $16900.00 | ($1500.00) | | +----------+------------------+-------------+------------+---+ | December | ($100.00) | $18500.00 | ($1700.00) | | +----------+------------------+-------------+------------+---+ | | | | | | +----------+------------------+-------------+------------+---+ | Totals: | $5400.00 | $116400.00 | ($7200.00) | | +----------+------------------+-------------+------------+---+ | | | | | | +----------+------------------+-------------+------------+---+ 1
14.2.25. Xbase File Format
The Xbase file format is a file format that includes a series of files of which one is a text file containing the data and the rest are index or other files. The data file consists of a header and then the records themselves.
Gnumeric only opens the data file.
| Name: | XBase data file format |
| Extensions: | .dbf |
| Compatible Programs: | dBase, Clipper, FoxPro, Visual dBase, Visual FoxPro, and numerous other database applications. |
| Import / Export: | Import only |
- Limitations
-
- Plugin
-
Supported by the 'XBase' plugin.
- Format Details
-
The xBase file format is a generic name for database files saved in the format used by Aston-Tate's (then Borland's) dBase database system. The system became widely popular and has been used extensively by other systems.
See the Xbase File Format Description by Erik Bachmann for more details on the xBase format.
14.2.26. XHTML File Format
The XHTML file format is a text file format with markup in the eXtensible Markup Language (XML) using a definition which mimics the Hypertext Markup Language (HTML). These files are designed to be viewed in a web browser.
Gnumeric can save the cell contents from a worksheet to a text file which consists of an XHTML file fragment containing only a <table> structure, designed to be inserted into another XHTML file.
| Name: | XHTML |
| Extensions: | .xhtml / .html |
| Compatible Programs: | Most modern web browsers such as Mozilla and Mozilla-Firefox |
| Import / Export: | Both |
- Limitations
-
- Plugin
-
Supported by the 'HTML & TeX' plugin.
- Format Details
-
The file is generated, encoded in UTF-8, in the World Wide Web consortium (W3C) XHTML 1.0 Transitional file format.
- Further Processing
-
These XHTML files can be opened by any text editor and can be viewed using any web browser such as Mozilla.
See Also: HTML Format
14.3. Opening Files
Opening an existing file into a Gnumeric workbook requires working through the File Open dialog. The user must select the file that they wish Gnumeric to open, possibly specifying a file format and character encoding.
-
Launch the File Open dialog.
In the menu, select the menu item.
-
Open the folder containing the desired file.
Navigate the folder hierarchy by double-clicking on the folders.
-
Select the desired file within the folder.
Click on the file name in the folder content area.
-
(Optional) Specify a file format type.
-
(Optional) Specify the character encoding.
-
Click on the button.
The remainder of this section explains these steps in greater detail, first, by describing the components in the File Open dialog and, then, by explaining each of the steps above in greater detail.
- 14.3.1. Using the File Open dialog.
- 14.3.2. The file formats which Gnumeric can read.
14.3.1. Using the File Open dialog.
Opening a file into a workbook is a relatively simple process. The only complications come from using the File Open dialog to find the desired file, from changing the automatic file format type recognition system, or from specifying a different character encoding than that chosen by Gnumeric. The first of these steps will become intuitive once the user understands the functioning of the dialog. The latter two steps are generally unnecessary and can be ignored by most users.
The next section explains in detail the different components of the File Open dialog and the subsequent section describes each step in the process of opening a file.
- 14.3.1.1. The components of the File Open dialog
- 14.3.1.2. The procedure to open an existing file.
- 14.3.1.3. Changing the list of bookmark folders.
14.3.1.1. The components of the File Open dialog
The File Open dialog allows the user to open an existing file into a Gnumeric workbook but requires that the user find the folder containing the file, select the file, and optionally define a file format type and a character encoding. The dialog also allows the user to change the list of bookmark folders to quickly access different parts of the file system.
The File Open dialog first appears as is shown in Figure 14-1 which also shows a label for each different component of the dialog.
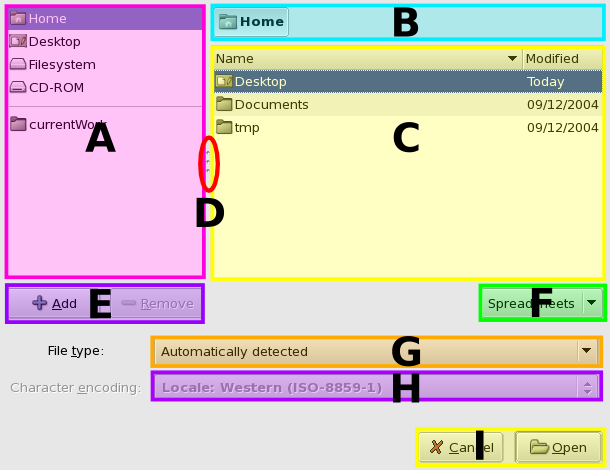
The different components of the File Open dialog, shaded with boxes of different colors and labeled with a letter.
The purpose of each labeled component in Figure 14-1 is explained below:
- A - The starting folder selection area.
-
This area allows the user to begin navigating the filesystem by choosing a starting folder. The navigation system in this dialog only allows users to select sub-folders of this starting folder so the starting folder must contain the desired file, possibly nested in one or more sub-folders.
The folders listed in this area include the standard folders provided by the system and a number of folders added, as bookmark folders, by the user. The standard folders provided by the system will vary for different machines and system administrators may have disabled access to certain branches of the filesystem. By default, the standard folders provided include the user's 'Home' folder, the user's 'Desktop' folder, a folder pointing to the root of the filesystem tree and folders for each of the removable storage devices attached to the computer. The user's home folder, on GNU and other UNIX like systems, this folder is usually known as ~ or ~user_account_name where the phrase user_account_name represents the account name used by the current user. This folder is often located at /home/user_account_name/ in the filesystem. The 'Desktop' folder is the folder which holds the files which are displayed in the background of the user's window. The 'Filesystem' folder is the top of the filesystem tree, which on GNU systems is also known as /. The list also presents peripheral or external devices. Below the standard folders, area A has a separator and the bookmark folders selected by the user. In Figure 14-1 the folder currentWork is a folder named by the user and added to the list of bookmark folders.
Understanding the file organization system.In order to understand how to change folders, it is first necessary to understand the system by which documents are stored. This system is called the 'filesystem'.
All documents are stored in a folder. Folders can contain files but can also contain other folders. Any folder therefore can contain several sub-folders, each of which may itself contain several sub-folders; the resulting structure is called a nested 'tree' with the original folder being the 'relative root' of that tree.
In GNU and UNIX systems, all of the files are stored in folders organized in a single, unified filesystem tree with a folder named '/' at the absolute root of the tree. Every file is accessible from this absolute root folder and, by default, this folder is provided as the choice named Filesystem with an icon of a disk drive in area A in the File Open dialog.
Navigating the directory tree from the single root folder would quickly become burdensome and the File Open dialog provides several other starting folders in area A. Two starting folders which are commonly provided are the 'Home' and 'Desktop' folders for the current user.
In a complex computer system, the absolute root folder may be hidden from the user and the starting folders accessible to the user may only provide limited access to the filesystem. Jointly, the starting folders provided should allow the users to access all the folders in which the user has permission to store files and to the folders which are designed to be read by the user.
Several starting folders may be provided when files can be opened from different filesystems. This will be the case when filesystem on other machines are accessible over a network or when Gnumeric is running on operating systems whose filesystems are not unified, such as the proprietary operating systems sold by Microsoft in which each disk drive has its own root named, for example, C:\ or D:\.
Additional starting folders can be added as 'bookmark folders' by the users themselves. These bookmark folders do not provide access to a different set of folders but merely provide efficient access to a folder and its sub-folders. These bookmark folders are easy to change to allow a user to work efficiently. These bookmark folders are listed, in area A, under the thin horizontal separator line. The creation and deletion of these bookmark folders is explained below, in Section 14.3.1.3 ― Changing the list of bookmark folders. .
- B - The folder hierarchy area.
-
This area displays the folder hierarchy starting from the starting folder selected in area A and ending in the current folder, the folder whose contents are displayed in area C, while displaying all the folders between the two. This area changes dynamically as the user changes to new folders. In the case shown in Figure 14-1, the user has selected their 'Home' folder as the starting folder in area A and has not navigated to any sub-folders.
- C - The folder content area.
-
This area displays the contents of the currently selected folder which is the rightmost folder shown in area B.
This list of folders and files is filtered.Not all of the sub-folders and files present in the folder area are shown.
Firstly, hidden folders and files, those that start with a leading period, are not displayed by default. These can be shown by placing the mouse pointer over area C, clicking with one of the secondary mouse buttons to raise the context menu, moving the pointer onto the menu entry, and clicking with the primary mouse button. This step will ensure that all the folders are displayed.
Secondly, the filtering rule defined in area F will limit the files displayed based on the characteristics of these files. By default, a filtering rule is applied which causes only those files present that have an extension commonly used for spreadsheet files. The rule can be changed to display all the files regardless of their extension, except possibly for the hidden files.
- D - The panel rearrangement handles.
-
These triple dots indicate that the mouse can be used to change the shape and size of the different areas in the dialog. These handles can be used by placing the mouse pointer above a handle, clicking and holding with the primary mouse button, then dragging the handle to a new position, and then releasing the mouse button.
- E - The bookmark folder list modification buttons.
-
These buttons will add or remove folders to or from the list of bookmark folders in area A. The button will add the folder currently selected in area C. The button will remove any bookmark folder that is selected in area A.
- F - The filter definition area.
-
This area contains a drop down menu with the different filters defined by the application. Filters are rules that limit the types of files which are displayed in the folder content area, area C.
By default, the File Open dialog starts with a filter named "Spreadsheets" which causes the folder content list to only show files which are recognized as files that Gnumeric could open.
The filter in area F can be changed by clicking on the area to open the drop down list and then selecting the filter named "All files". This filter applies no rules, essentially disabling any filtering operation, and lists all the files in the currently selected folder. Note, however, as explained in the warning given in the section explaining area C above, that any files starting with a leading period are not shown. To display such 'hidden' files, the user must use the context menu available in area C.
- G - The file format type selection area.
-
This area provides a drop down list of all the file formats provided by the Gnumeric program itself and by all the currently active plugins.
By default, Gnumeric is configured to automatically recognize the type of each file selected by the user. This recognition system is sophisticated and generally works. The best strategy is to try opening the file using this automatic recognition strategy and, only if the automatic recognition system fails, close the worksheet with the mangled file and re-try to open the file a second time but manually selecting the file type in the second attempt.
The file formats which can be selected are those listed in Section 14.3.2 ― The file formats which Gnumeric can read. below. Each of these formats are explained in detail in Section 14.2 ― File Formats.
If the file format type named "Text import (configurable)" is opened, this will start the text import procedure. Section 14.4 ― Importing Text Files explains this procedure in complete detail.
- H - The character encoding selection area.
-
This area provides a drop down menu which allows the user to specify the encoding which Gnumeric must use to interpret the characters in text files. This menu is only enabled for the two text file formats: "Comma or Tab Separated Values (CSV/TSV)" and "Text Import (configurable)". This menu is disabled for all other file types because Gnumeric automatically detects the encoding for those files.
A character encoding is a system to relate the binary digits contained in a computer file to the characters of a textual script. All computer files consist only of binary digits so some system is required to determine this relationship. Where early computers used simple encoding systems which only supported the characters commonly used in English, most systems are now standardizing on the UTF-8 encoding scheme which relates the binary digits in computer files to characters defined in the Universal Character Set, a set which is still being defined but will include all the characters in every language and many other useful symbols for mathematics, science, music and literature. Section 14.4.1.1 ― Character Encodings contains a brief explanation of character encoding, and discusses the encodings available in Gnumeric.
The character encoding can be set using the drop down menu in area H. By default, the encoding is set for the locale of the user. The locale is set by the operating system and defines the language, time zone and other geographic related preferences of the user. The character encoding is changed by clicking on the drop down menu button in area H, that is by placing the mouse pointer over this menu and clicking on the primary mouse button, and then navigating the menu to select the new encoding, that is by moving the mouse through the menus and clicking on the name of the new encoding. Gnumeric will then use this encoding to open the text file.
- I - The button area.
-
The button area provides two buttons, the and the buttons. Clicking the button will dismiss the dialog and return the user to the worksheet. Clicking the button will cause the selected file to be opened into a worksheet, using either the automatic file format type detection or the file format type specified if one has been selected, and using the character encoding scheme if one has been selected.
The procedure required to open a file into a workbook using this dialog is presented next.
14.3.1.2. The procedure to open an existing file.
Opening an existing file into a workbook requires selecting the folder containing the desired file, selecting the file within this folder, and optionally selecting the file format type and character encoding.
-
Launch the File Open dialog.
The File Open dialog can be launched using three alternative approaches.
All three methods will result in the equivalent action, launching the File Open dialog to allow the user to find the file that they wish to open.- Using the Menus
-
Select, in the menu, the menu item.
- Using the Standard Toolbar
-
Click on the button:

- Using a Keyboard Shortcut
-
Type the combination Ctrl+o, typing both keys simultaneously.
-
Navigate the file system to open the folder with the file.
Changing folders involves selecting a starting folder in area A which contains the folder with the desired file, and then double-clicking on the folders listed in area C until the folder containing the file has been reached. The folder hierarchy listed in area Bcan also be used to navigate up the hierarchy if a folder was opened by mistake. As explained below, a user can move around the hierarchy with as many folder selections as they need to reach the folder containing the file the user desires to open.
To select a new folder, one of the starting folders which contains the desired folder must first be selected and then the hierarchy must be navigated to find the desired folder, and this folder must be opened to expose its contents. As explained below, a user can move around the hierarchy using as many changes as they need to choose the folder in which to save their Gnumeric file.
-
Select a starting folder in area A.
The first step in choosing a new folder requires selecting, in area A, a starting folder which contains the desired folder. The new starting folder is chosen by placing the mouse pointer over the folder name and double clicking (click twice rapidly without moving the mouse) with the primary mouse button. This will change the leftmost button in area B and change the folders and files listed in area C to list the contents of the starting folder which was just selected.
-
Navigate the filesystem to reach the desired folder using area C.
The next step involves descending the folder tree to reach the desired folder. This requires double clicking the sub-folder of the staring folder which contains the desired folder and continuing through the whole hierarchy until the desired folder is reached. After each double click, the selected folder is added as the right most button in area B and the contents of the selected folder are shown in area C. Once the desired folder is reached, it must be opened in the same way, so that its contents are listed in area C and the file can then be saved into this folder by clicking on the button.
-
Navigating back up the folder tree using area B.
If the sub-folder selected in area C does not contain the branch of the folder tree leading to the desired folder, the buttons in area B can be used to jump further up the folder tree but only as far as the starting folder selected in area A. Area B provides a list of buttons with the names of all the folders between the starting folder listed in area A and the currently selected folder. By clicking on one of these buttons, that is by placing the mouse pointer over the button and clicking with the primary mouse button, the folder listed on the button will be opened in area C so that the selection process can restart from this branch.
-
-
Select the file.
The file must be selected by placing the mouse pointer over the filename in area C and clicking with the primary mouse button.
The file can be opened and the dialog dismissed by selecting the file with a double click of the primary mouse button. The last two steps are optional and, if configured appropriately, the file can be selected and opened simply by double clicking on the file name.
-
Optional: Select the file format type.
Gnumeric can automatically recognize the file format type. Alternatively, the file format can be specified explicitly by clicking on the drop down list button in area G and scrolling down the list to the desired file type.
If the file format type named "Text import (configurable)" is opened, this will start the text import procedure. Section 14.4 ― Importing Text Files explains this procedure in complete detail.
-
Optional: Determine the file character encoding.
For text files the character encoding must be specified. By default, Gnumeric takes the character encoding appropriate to the user's locale. This encoding scheme can be changed by clicking on the drop down menu button in area H and navigating the menus to find the desired encoding.
-
Click the button.
Finally, the button must be pressed by placing the mouse pointer over the button and clicking with the primary mouse button.
The file will be opened in a new window. If the selected file format was "Text import (configurable)" the Text Import druid will be opened. This druid is explained in great detail in Section 14.4 ― Importing Text Files.
14.3.1.3. Changing the list of bookmark folders.
The list of starting folders shown in area A of Figure 14-1 may contain starting folders selected by the user. These folders are called 'bookmark folders' and are listed in area A below a thin horizontal separator line. For example, Figure 14-1 contains a folder named currentWork which is a bookmark folder selected by the user.
These bookmark folders can be added in two ways. A folder which is selected in area C can be added as a bookmark by clicking on the button in area E.
Alternatively, the folder can be dragged from area C into area A. The folder can be dragged by placing the mouse pointer over the folder name in area C, clicking and holding the primary mouse button, moving the mouse pointer to area A and releasing the mouse button. As the mouse pointer is moved from area C to area A, a small icon of the folder will move with the mouse pointer.
Any bookmark folder can also be removed from the list of starting folders presented in area A. A bookmark folder can be removed by clicking on the folder name in area A and then clicking on the in area E.
14.3.2. The file formats which Gnumeric can read.
Gnumeric can open files which have been created in several formats by other spreadsheet programs or databases. The details of these formats are provided in Section 14.2 ― File Formats and the name of each file type in the table below skips to the appropriate section of Section 14.2 ― File Formats. The opening of text formatted files is described in Section 14.4 ― Importing Text Files. Gnumeric can also import text data or HTML and XHTML tables through the clipboard mechanism, as is explained in Section 5.7.4 ― Cut and Paste Between Gnumeric and Other Applications.
Most of these formats are provided by plugins, which are independent, configurable modules. If a format described below does not appear in the File Open dialog, this may be because the appropriate plugin has not been configured or started. This can be verified by examining the list of plugins which are currently running in the Plugin Manager dialog.
The Plugin Manager dialog lists the plugins which are currently in use and provides a way to start plugins which are currently disabled. The Plugin Manager can be started by selecting, in the menu, the menu item; see Section 13.4 ― Plugins for more information.
| Format | Extension |
|---|---|
| Gnumeric | .gnumeric / .gnm |
| Applix | .as |
| Comma Separated Values | .csv |
| Data Interchange Format | .dif |
| GNU Oleo | .oleo |
| HTML | .html / .htm |
| Linear and Integer Program | none / .mps |
| Lotus 1-2-3 | .wk1 / .wks |
| Microsoft Excel Old Binary | .xls |
| Microsoft Excel New Binary | .xls |
| Microsoft Excel 2003 XML | .xls |
| Microsoft Excel Office Open XML | .xlsx |
| OpenOffice.Org / StarOffice (OASIS ODF/IS26300) | .ods / .odt |
| OpenOffice.Org / StarOffice Old Format | .sxc / .stc |
| Plan Perfect | .pln |
| Quattro Pro | .wb1 / .wb2 / .wb3 |
| SC/XSpread | none / .sc |
| Multiplan (SYLK) | .sylk / .slk |
| Tab Separated Values | .tsv / .tab |
| Text Formats | .txt / .text |
| Xbase | .dbf |
14.4. Importing Text Files
Gnumeric can import data which is organized as text fields structured in some systematic fashion either from a file or from the clipboard. Importing structured text may require extensive intervention on the part of the user so Gnumeric provides a Text Import druid, which is a three paneled dialog with configuration options. For text imported from files, this druid appears after the file has been imported, using the menu item in the submenu of the menu as described in Section 4.2.10 ― Data Menu. For text imported from the clipboard, the druid appears when a user attempts to paste the text into a worksheet, as is explained in Section 5.7.4 ― Cut and Paste Between Gnumeric and Other Applications.
The text import druid contains three panels but the middle panel differs depending on the structuring system used, either with data fields separated by a special character or with data fields occurring at equally spaced intervals in each line. The first panel allows the user to configure the character encoding, line break characters, structuring system, and line range. The second panel allows the user to define the columns by either, for separated data, setting the separating character and text delimiting character, or, for fixed space data, by setting the column spacing. The third panel allows the user to select which columns to import and define their data types.
- Launch the Text Import druid using, in the , the and selecting the "Text import (configurable)" file format type.
- Define the character encoding of the text block.
- Define the characters indicating the breaks between the lines.
- Select the line range from the text block to be imported.
- Go to the second panel, which will be different for data structured by separating characters and data structured by fixed spacing.
- (For separated data) Define the separating character.
- (For separated data) Define the character grouping a text field.
- (For fixed width data) Define the field widths.
- Go to the third panel.
- Configure the inclusion of empty outside columns.
- Select the locale that will influence the formatting of the numerical elements in each column.
- Select the numerical formats for the data in each columns.
- Select the columns to be included in the imported block.
- Click on the button.
This explanation of the Text Import druid will first start with a discussion of text files including character encodings and line break delimiters. The explanation will then cover the various strategies used to structure numeric data in text files. Following these discussions, the components of the druid will be presented and, finally, a detailed explanation of each step in the use of the druid will be presented.
14.4.1. The complexities of text format files
The use of text format files to store and transmit data for use in a spreadsheet involves three somewhat complex decisions which determine how the file expresses and separates each data value. These complexities must be understood for a user to be able to use the Text Import druid effectively. These complexities exist because of the limitations of early computers and because or the historical development of computer systems by different manufacturers and programmers, in different countries, targeting different types of users, speaking different languages.
The first complexity involves the different systems which relate the contents of a computer file to the characters in a written language. All text files on a computer consist of a long sequence of binary digits. Text files are files in which these digits are used to indicate different textual characters. Character 'encodings' are standardized systems which relate the binary digits in a computer file to a formal system of characters which includes both text glyphs (shapes) and formatting indicators. Each encoding defines a way to interpret the binary digits and uses the characters from a particular character set. The alternative character encoding strategies are explained in greater detail in Section 14.4.1.1 ― Character Encodings, below.
The second complexity involves the decision of how to separate the characters in a file into different lines. Text files explicitly determine the end of each line of a file with a specific character or sequence of characters. The complexity involves the particular character sequence used to determine the end of each line. Different conventions have been used in different computer systems. The alternative line breaking strategies are explained in greater detail in Section 14.4.1.2 ― Line break delimiters, below.
The third complexity involves the decision of how to separate the characters in each line into separate value fields. Again, different strategies exist. These can be separated into two broad categories: strategies which use a character or sequence of characters to separate the values, so called 'delimited' or 'separated' strategies, and strategies which use the position of the character in the line to separate the values, so called 'fixed-width' strategies. The alternative data structuring strategies are explained in greater detail in Section 14.4.1.3 ― Data Structuring Strategies, below.
Fortunately, the Gnumeric Text Import druid provides users with a way to preview the information in a text file. This enables users to change the settings which determine each of these three conventions until the text in the preview correctly shows the contents of the data file. Therefore, while the details of these three steps are complex, the practical impact on users is minimal. Users can simply experiment until the file appears correct without having to understand each of these complexities in detail.
- 14.4.1.1. Character Encodings
- 14.4.1.2. Line break delimiters
- 14.4.1.3. Data Structuring Strategies
14.4.1.1. Character Encodings
The use of text files to store data in a structured fashion for use by spreadsheet programs, and more generally all text files, require some scheme to relate the binary number in the computer file itself to the characters of a written language. Such schemes are called 'encodings'.
The origin of computers led to the invention of a number of different encoding schemes. Due to the limitation of early computer hardware, these encoding schemes all restricted themselves to character sets which contained only the most essential characters of the English language. The desire to support characters which were not in this basic set of characters led to the creation of new encoding schemes, many of which restricted themselves to the characters in specific languages. One encoding scheme, called UTF-8, has now emerged as the best encoding scheme for the future for a multitude of reasons including its ability to co-exist with current operating systems and its ability to encode all of the characters in the largest set of characters which has been consistently defined, the Universal Character Set. However, the existence of the diversity of encoding schemes means that for the foreseeable future, files will be created and distributed using several different schemes. This is especially true for files containing text in languages other than English.
This complex situation generally does not impact users. Gnumeric has been designed to deal with most of the complexity. Many kinds of files, such as the Gnumeric file format itself, describe their encoding scheme internally in such a way that it can be easily recognized. Gnumeric also provides an easy approach to changing the encoding scheme in case this proves necessary.
Encoding schemes merely prove a hindrance to users when opening files. There is no danger that data be lost or that any other serious problem arise by selecting the wrong scheme. If the wrong scheme is selected, either the file will contain characters which are nonsensical and Gnumeric will open an error dialog asking the user to select a different encoding scheme, or the preview area will display nonsensical characters. These nonsensical characters may simply be characters grouped together which do not occur in any language, such as "åÕÛÛÞ", or may be characters for which a graphical representation (a glyph) does not exist in the font being used and is therefore displayed using a small box with four numbers inside. Each of these errors indicates that the encoding scheme used to read the file was not the same encoding scheme as was used to create the file. The difficulty is then to determine what encoding scheme to use. A simple process of trial and error should lead to picking the right scheme.
A basic strategy to find the right encoding for a file being imported into Gnumeric is, first, to use the scheme proposed by Gnumeric and, then, to hunt for the correct encoding. The default encoding scheme is the one defined by the locale setting of the user and this is also the default scheme Gnumeric uses to create text files. If the default encoding is incorrect, the correct encoding must be found by trial and error. One strategy to use is to examine the major western encodings and then the major regional encodings. The major western encoding schemes are ASCII, ISO-8859-1, and UTF-8, but ASCII is a subset of the other two so it does not need to be tried on its own. The major regional encodings are the IS0-8859-x schemes since these have become quite popular in GNU operating systems. Alternatively, the various character sets used by the Microsoft operating systems can be attempted. The encoding schemes are listed under "Western", "Unicode", and the alphabet names.
The World Wide Web has many resources dedicated to explaining encoding systems and other related information. One of the best sites discussing UTF-8 and Unicode is the UTF-8 and Unicode FAQ for UNIX/Linux page maintained by Markus Kuhn. The Unicode project has a web site which includes an online copy of their standard character set. A discussion of the ISO-8859 family of encodings can be found at a page titled: "The ISO-8859 Alphabet Soup", which may alternatively be found here. A similar discussion on Wikipedia, focusing on the western alphabets, can be found here.
14.4.1.2. Line break delimiters
The use of text files to store data in a structured fashion for use by spreadsheet programs requires a scheme to separate each line of the file. Structured text files rely on the files having explicitly defined rows within the file as one component in the structuring system. Each of these rows is defined by a character sequence indicating the end of a row.
Two characters that are part of the ASCII code, an early encoding that became a widely followed standard, were included to help define the end of the line. These are the 'linefeed' character and the 'carriage return' character, named after the two processes which occur when a typewriter starts a new line: first the typewriter barrel rolls - the linefeed - then the whole carriage with the sheet of paper moves back to the starting point -the carriage return. In the same way that different computing systems have used different encoding schemes, three different approaches became common for defining the end of the line.
In GNU operating systems and other systems that inherit from the UNIX legacy, the end of a line was defined simply using the 'linefeed' character. The pre-OSX Macintosh operating system chose instead to use only the 'carriage return' character. The Windows operating system uses both characters in the sequence 'carriage return' then 'linefeed'.
A user opening a file into Gnumeric will see, in the preview area of the Text Import druid, whether or not the line breaks have been recognized correctly and will be able to alter the recognition settings. An incompatible setup will either yield a single unbroken line of text, lines of text with extra, empty rows between them, or lines of text with extra symbols at the start or end of each line.
The correct line break delimiters can be established by checking or unchecking the alternatives. The preview area will then show the result of the file interpreted with these settings.
14.4.1.3. Data Structuring Strategies
The use of text files to store data in a structured fashion for use by spreadsheet programs also requires some scheme to separate each value within every line. Two different approaches are used to separate these values. The first strategy, uses a particular character or character sequence to denote the start and end of each value. Such strategies are called 'Separated Value' or 'Delimited Value' systems. The second strategy places each value stating at a specified position in the line. Such strategies are called 'Fixed Width' strategies because they inherently require that each value have a pre-determined size.
Separated Value structuring systems distinguish the contents of each value using pre-determined characters to separate the values. Certain characters have become common in such schemes, for-example 'Comma Separated Value' files use a comma character to separate values while 'Tab Separated Value' files use a tab character. Gnumeric allows the user to define the value separator to be any one of several common characters or a specific sequence of characters, either on their own or in combination. For example, a file could use both space characters and tab characters to separate values. Similarly, a file could be read which used the entire word 'STOP' to separate values like the common scheme to separate sentences in a telegram.
Separate Value structuring systems often also include a method to surround a single text value which may itself contain the character used to separate values. The quote character is often used in this role but Gnumeric allows users to configure any character in this role. For example, a file which used the comma to separate values could nonetheless contain a value like "Zoe, Sally, Dodji" if this value had appropriate text indicating characters at either end.
Fixed Width structuring systems are common formats for the output of database tables since the contents of these tables have often been defined as variables of a particular size. To import these files, users must specify exactly the start of each column so that the importer can separate the values on each row.
14.4.2. The Components of the Text Import Druid
The Text Import druid consists of three panels with the middle panel differing according to the type of data structuring used.
The first panel allows users to configure the character encoding used by the file, to determine the character sequences used to separate lines, configure the type of structuring being used and select the lines of the file to import. The second column allows the user to define the separation strategy used for each value. For separated value files this involves defining the separating character sequences and the text indicating character. For fixed width files, this involves defining the width of each column. The third panel allows the user to select the columns to be included during the import and to select the format of the values in each column.
Users navigate the Text Import druid by clicking on the button on each panel after they have configured the settings properly. The third panel contains a which causes the file to be imported to a workbook using all the settings as they are configured.
14.4.2.1. The first panel of the Text Import Druid.
The first panel of the Text Import Druid allows users to set the file encoding, to determine the character sequences used to separate lines, configure the type of structuring being used and select the lines of the file to import.
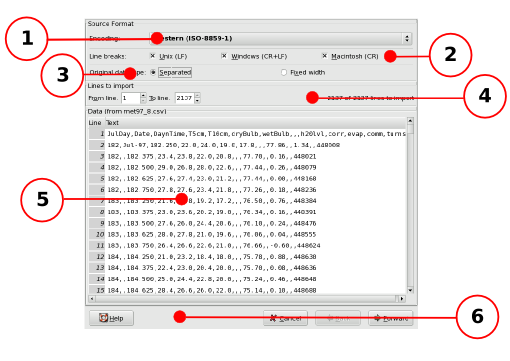
The different components of the first panel of the Text Import druid with each component labeled with a callout.
The purpose of each labeled component in Figure 14-2 is explained below:
- 1 - The file encoding selection menu.
-
This drop down menu provides a list of encoding schemes for the characters in the text file. By default, Gnumeric selects the encoding scheme used by the locale of the user. See Section 14.4.1.1 ― Character Encodings for more details.
- 2 - The line break character selector.
-
These three check boxes can be selected individually or together to define the sequences which will be interpreted as line break indicators. Generally, selecting all three boxes will produce the correct results.
The errors produced if the wrong combination of boxes is selected will include the entire file being placed on a single line, empty lines appearing between the lines of the file, or undefined symbols appearing at the beginning or end of almost every line. See Section 14.4.1.2 ― Line break delimiters for more details.
- 3 - The data structuring system selector.
-
These two push buttons allow the choice between the two different structuring schemes, data structured by placing a separating character between the data values and data organized in fixed width columns. Note that this choice will determine which panel will be shown as the second panel of the druid. See Section 14.4.1.3 ― Data Structuring Strategies for more details.
- 4 - The line range spinbuttons.
-
These two spin buttons allow the user to select the start and end rows for the data import. The spin boxes can be used either by typing a new value in the text entry area where the numbers are displayed, or by using the mouse button to click on the up arrow to increase the number and the down arrow to decrease the number.
For instance, if the text file contained a large header area with meta information, this header could be excluded from the data imported to the Gnumeric worksheet by increasing the number of the starting, "From", line.
- 5 - The preview area.
-
This area displays a preview of the file as it will be interpreted when the settings that are currently selected in this first panel are applied.
- 6 - The button area.
-
These four buttons allow the user to navigate the druid. The button should open the Gnumeric manual to this section. The button will dismiss the dialog and return the user to the worksheet. The button is disabled since this is the first panel of the druid and the button will bring up the next panel in the druid.
14.4.2.2. The second panel of the Text Import Druid used for separated data
The second panel of the Text Import Druid used for separated data allows the user to configure the character sequences used to separate the values in each row and to configure the text delimiting characters. Gnumeric, by default, guesses which characters are being used to separate values and pre-sets those characters. The user can, however, reconfigure these characters.
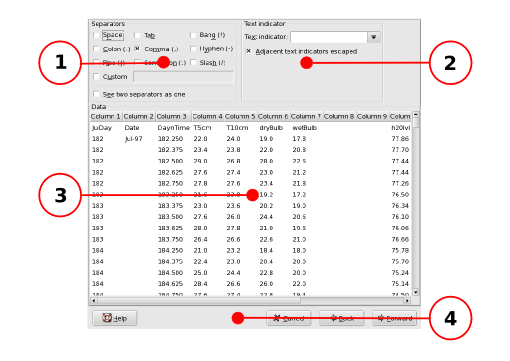
The different components of the second panel of the Text Import druid for separated data with each component labeled with a callout.
The purpose of each labeled component in Figure 14-3 is explained below:
- 1 - The separator definition area.
-
This are allows the user to define the characters used to separate data value fields within each row. The checkboxes can be pressed to add or remove characters from those treated as separators. Additionally, the 'custom' type allows the user to define either other single characters, or a particular character sequence used to separate values. The preview area in the panel will show the file processed with the rules which have already been applied.
Generally, this type of file structuring uses a single character to separate fields but it is possible to use either several different characters or to use a sequence of characters. For example, it would be possible to use the old telegraphic convention of separating phrases with the word 'STOP' by selecting the 'custom' separator type and entering the character sequence 'STOP' in the text field.
This area also includes a checkbox enabling two separator sequences that immediately follow one another, to be treated as a single separator. This option will only be useful where data is imported with one or more completely empty columns and no partially filled columns. If this option is checked and the data file has partially filled columns of data, the columns will be jumbled during the text import operation.
See Section 14.4.1.3 ― Data Structuring Strategies for more details.
- 2 - The text indicating character area.
-
Separated value files often additionally define a character used to indicate the start and end of a data element which should be considered a single text entry. This strategy allows the inclusion of text entries which include the value separator.
For example, a file which is structured as a comma separated value file, could use the double quotation mark to delimit text values and would then be able to include text values such as: 'Zoe, Mark, Sally'.
- 3 - The preview area.
-
This area displays a preview of the file as it will be interpreted when the settings that are currently selected in the first and second panels are applied.
- 4 - The button area.
-
These four buttons allow the user to navigate the druid. The button should open the Gnumeric manual to this section. The button will dismiss the dialog and return the user to the worksheet. The button will take the user back to the first panel, without, however, changing the settings in this second panel. The button will bring up the next panel in the druid.
14.4.2.3. The second panel of the Text Import Druid used for fixed width data
The second panel of the Text Import Druid used for fixed width data allows the user to define the widths of each column to be imported. Gnumeric provides a mechanism to automatically guess the widths of the columns and allows the user, using the mouse, to define the widths of the columns.
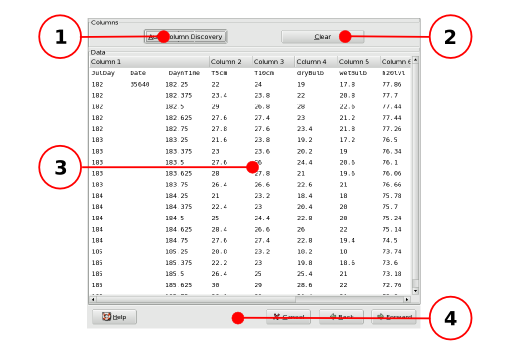
The different components of the second panel of the Text Import druid for fixed width data with each component labeled with a callout.
The purpose of each labeled component in Figure 14-4 is explained below:
- 1 - The automatic column discovery button.
-
This left most button, named , will cause Gnumeric to scan the file an attempt to assign the columns automatically. The example presented in Figure 14-4 shows one result after this button has been pressed: many of the columns were discovered automatically, but the second and third columns were misidentified. Nonetheless, the automatic mechanism provides a useful starting point. The definition of the columns can be refined using the methods described below.
- 2 - The column definition clearing button.
-
This right most button, named , will clear all the column definitions and reset the file to a single column. This button should be used cautiously since there is no way to reverse its action and any carefully prepared column definition layout will be irretrievably lost.
- 3 - The preview and column width definition area.
-
This area acts as both a preview area and an area where users can define the columns widths.
As a preview area, this area displays a preview of the file as it will be interpreted when the settings that are currently selected in this first panel are applied.
This area can also be used to define column widths. When the panel first appears, a single column will be defined. The automatic column discovery mechanism may split this single column into many more columns. The mouse can then be used to further divide columns or to join previously separate columns.
A new column can be defined by placing the mouse pointer where the column should start and double-clicking with the primary mouse button. This will split the column which used to contain this position and add a new column starting at this location.
To remove the definition of a column which already exists or to alter the ending position of a column, the context menu must be used. The context menu appears by clicking with one of the secondary mouse buttons. A column which has already been defined can be merged with the column on the left or right using the or menu items. The size of a column can be increased by placing the mouse pointer inside the column area or header and using the or menu items, respectively. Either of these will change the width of the column by changing the right hand end of the column.
The context menu can also be used to define new columns using the menu item but the double-click approach described above should be easier.
- 4 - The button area.
-
These four buttons allow the user to navigate the druid. The button should open the Gnumeric manual to this section. The button will dismiss the dialog and return the user to the worksheet. The button will take the user back to the first panel, without, however, changing the settings in this second panel. The button will bring up the next panel in the druid.
14.4.2.4. The third panel of the Text Import Druid
This panel allows users to select and format the columns to be imported to the Gnumeric workbook. The first button allows the exclusion of empty columns on either of the outer sides of the columns with data. The second button allows the user to define the locale used to interpret the values in the file. The remaining area allows the user to predefine the data format to be used for all the values in each column. This area also allows the users to select which columns in the file will be imported to the Gnumeric worksheet. Finally, this panel provides the which is used to dismiss the dialog and import the file.
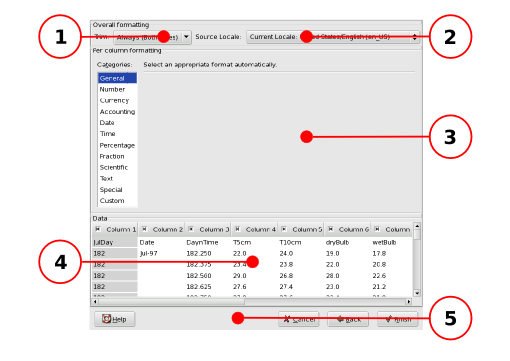
The different components of the third panel of the Text Import druid with each component labeled with a callout.
The purpose of each labeled component in Figure 14-5 is explained below:
- 1 - The trim of empty outer columns drop down list button.
-
This button provides a list allowing the user to select whether to trim any outer columns which are completely empty. The choices are to delete the columns on both sides, on neither side, or on one side only. This will only affect columns which have been previously defined but which contain no data values at all.
- 2 - Locale definition for import drop down menu button.
-
This button provides a list of locales which can be set. The chosen locale will affect how numeric values are interpreted when then are imported. For instance, the locale will define the character expected as the decimal separator which is the period character (.) in some locales, and the comma character (,) in others. These locales generally then use the other character as the spacer grouping the digits in thousands.
- 3 - The column data format selection list.
-
This list allows predetermining the format which Gnumeric will assign to each of the values in the columns selected below. Cell data formats are explained in Section 5.10 ― Formatting Cells.
To use this list, first, one or more columns must be selected in the preview area below, then, a data format in this list can be selected, and finally any details of the format can be configured. Number formats for instance allow the user to force numbers to contain fixed number of digits after the decimal point.
- 4 - The column selection, inclusion, and file preview area.
-
This area allows users to select columns which will be preformatted, to select which columns to include in the import and to preview the file. Each single column can be selected by clicking with the mouse pointer on the column header. Any single column can be excluded from the data imported to the Gnumeric worksheet by clicking in the checkbox in the column header to remove the check mark. The area also provides a preview of the data in the text file showing the effect of the with the current configuration.
- 5 - The button area.
-
These four buttons allow the user to navigate the druid. The button should open the Gnumeric manual to this section. The button will dismiss the dialog and return the user to the worksheet. The button will take the user back to the second panel, without, however, changing the settings in this third panel. The button will dismiss the druid and cause the file to be imported into a new worksheet using the selected configuration parameters.
14.5. Saving Files
There are several ways to save a Gnumeric workbook that is currently open.
Existing files can be saved directly but this process does not allow a user to change any settings to the file creation process.
If the workbook has already been saved to a file or if the workbook was opened from a file that already existed, Gnumeric will simply overwrite the file with the newer version.
- Using the Menus
-
Select, in the menu, the menu item.
- Using the Standard Toolbar
-
Click on the button:

- Using a Keyboard Shortcut
-
Type the combination Ctrl+s, typing both keys simultaneously.
Users wishing to save an existing file to a new file must invoke the Save As... dialog. The Save As... dialog can be invoked at any time to save the current workbook to a new file with either a different name or a different file format type. This dialog is automatically launched when a user attempts to use one of the methods described above to save a workbook which does not already have an existing file.
The Save As... dialog asks the user to provide a name for the file to be created, to select a folder in which to place the new file, and to select a file format type for the file.
-
Launch the File Save dialog.
In the menu, select the menu item.
-
Name the file. Open the folder containing the desired file.
In the text entry area, enter the file name.
-
Select the desired folder in which to save the file.
Select one of the standard locations to open the file.
-
Specify a file format type.
-
Click on the button.
The remainder of this section explains these steps in greater detail, first, by describing the components in the File Save dialog and, then, by explaining each of the steps above in greater detail.
14.5.1. Using the File Save dialog.
Saving a workbook to a file can be a simple process, depending on the folder in which the file is to be saved. If this folder is in the predefined list of standard folders and user bookmark folders, the file can be created with the compact File Save dialog. The components of the compact File Save dialog and the procedure to save a workbook to a file in the predefined list of folders are explained next.
However, when the workbook is to be saved to a file created in a folder which is not in the preselected list, the expanded File Save dialog will be required. The components of the expanded File Save dialog, the procedure for saving files in a different folder, and an explanation of bookmark folders and their use are given further below.
- 14.5.1.1. The components of the compact File Save dialog.
- 14.5.1.2. The basic file saving procedure.
- 14.5.1.3. The extra components in the expanded File Save dialog.
- 14.5.1.4. Changing the currently selected folder.
- 14.5.1.5. Adding a folder.
- 14.5.1.6. Changing the list of bookmark folders.
14.5.1.1. The components of the compact File Save dialog.
The File Save dialog allows the user to save a workbook into a new file but requires that the user provide a name for the file, select the folder in which to save the file, and select a file format type to use for this file. This dialog also provides a way to navigate the folder hierarchy as will be explained further below.
The File Save dialog first opens in a compact layout. The different areas of the dialog in this compact layout are shown and labeled in Figure 14-6.
The purpose of each labeled area will be explained below:
- A - The naming area.
-
This area is used to give the file its name. This is a standard text entry area allowing all the basic editing commands. The cursor can be moved left or right using the keyboard arrow keys. The cursor can be placed anywhere in the text by placing the mouse pointer where the cursor should go and clicking with the primary mouse button. The mouse can also select part or all of the text with a click and drag. The keyboard shortcuts for copying, Ctrl+c, cutting, Ctrl+x, or pasting, Ctrl+v, all work. The dialog uses filename matching to guess file names based on the files already in the parent folder.
- B - The folder selection area.
-
This area provides a drop down list of previously selected folders including the standard folders and the folders which have been bookmarked by the user. The area will be disabled if area D has been selected to expand the dialog.
The desired folder can be selected by moving the mouse pointer over the button, clicking and holding the primary mouse button, dragging the mouse pointer onto the name of the desired folder and releasing the mouse button. The new folder name will appear on as the name on the button.
- C - The file format type selection area.
-
This area provides a drop down list of all the file formats provided by the Gnumeric program itself and by all the currently active plugins.
If the file format type named "Text export (configurable)" is opened, this will start the text export procedure. Section 14.6 ― Exporting Text Files explains this procedure in complete detail.
- D - The dialog expansion area.
-
This area will alter the dialog to expand or collapse it. When expanded the dialog provides a way to select any folder accessible on the system, to create new folders and to add and remove bookmark folders from the user's bookmark folder list. When the dialog is expanded, the small arrow will point downward, the areas showing in Figure 14-7 will appear and area B will be disabled.
- E - The button area.
-
This area provides two buttons, the and the buttons. Clicking the button will dismiss the dialog and return the user to the worksheet. Clicking the button will cause a file to be created with the currently selected name, parent folder and format. If the selected file already exists, Gnumeric will open a confirmation dialog since the command will obliterate the previously existing file.
The procedure to save a file using this dialog in its compact form is present next, in Section 14.5.1.2 ― The basic file saving procedure. . The components of the dialog in its expanded layout, converted by clicking in area D when the File Save dialog is in its compact form, will be explained further on, in Section 14.5.1.3 ― The extra components in the expanded File Save dialog. , followed by sections explaining the use of the dialog in this expanded layout.
14.5.1.2. The basic file saving procedure.
Saving a workbook to a new file requires providing name the file, selecting a folder in which the file will be placed, and selecting a file format type.
The default action, if a user simply opens the File Save dialog and clicks on the button, is to name the file Book1.gnumeric incrementing the number for each new file created, to save the file in the user's home folder, and to create a file in the Gnumeric file format.
If the user provides a name for the file to be saved which is the same as the name of a file that already exists, Gnumeric will open up a confirmation dialog asking the user if they really want to overwrite the existing file. If the user then clicks on the button, the existing file will be destroyed and the new file created in its place.
-
Open the File Save dialog.
First, the dialog must be opened using either of the two following methods:
Two alternative ways to open the File Save dialog.- Using the Menus
-
Select, in the menu, the menu item.
- Using a Keyboard Shortcut
-
Type the combination Shift+Ctrl+s, typing all three keys simultaneously.
Both methods will launch the File Save dialog to allow the user to name the file, select a folder (also called a directory) for the file and choose a file format type. This dialog will also open automatically the first time a new workbook is saved.
-
Select a name for the file.
Next, a name must be given for the file. Gnumeric provides a default name but, when the dialog is first opened this name is highlighted indicating that it is already selected. Therefore, a user can simply start typing a new name and the first character entered will delete the name given by default. The file name field is presented as area A in Figure 14-6.
If typing a name does not have any effect, the 'focus' was probably inadvertently changed from the text entry area. Focus can be returned to the area by placing the mouse pointer over the box and clicking the primary mouse button. All the standard keyboard editing commands work in this text area and the mouse can be used to select text or to move the cursor location.
-
Select a folder in which to save the file.
Then, the folder in which to save the file can be chosen from the drop down list shown as area B in Figure 14-6.
Using this list requires placing the mouse pointer above the list button and clicking with the primary mouse button to open the list. The desired folder can then be selected by moving the pointer down the list and clicking again with the primary mouse button. The second click will close the drop down list and change the selected folder. Instead of the two mouse clicks, the entire operation can be replaced by a click-hold, drag and release, where the first mouse click is replaced by the click-and-hold and the second mouse click is replaced by the release.
This list only provides a limited number of choices including several standard folders and any bookmark folders the user has previously added to the file selector. Other folders can be chosen, new folders can be created, and the list of bookmark folders available can be changed, by clicking in area D to change to the expanded dialog, as will be explained further below, in Section 14.5.1.4 ― Changing the currently selected folder. , Section 14.5.1.5 ― Adding a folder. and Section 14.5.1.6 ― Changing the list of bookmark folders. .
-
Select a file type.
Next, the desired file type must be selected. Area C in Figure 14-6 provides a drop down list of file types. The process for using this list is the same as was described in the previous step. The file types are listed below in Section 14.5 ― Saving Files and explained in detail in Section 14.2 ― File Formats.
If the file format type named "Text export (configurable)" is opened, this will start the text export procedure. Section 14.6 ― Exporting Text Files explains this procedure in complete detail.
-
Click the button.
Finally, the button must be pressed by placing the mouse pointer over the button and clicking with the primary mouse button.
This basic procedure does not allow a user to save the file into folder other than one already provided. An expanded procedure is needed to explain how to save a file into other folders in the file system. The next section explains the extra elements provided when the File Save dialog is expanded and that section is followed by a step-by-step procedure explaining how to use this expanded dialog.
14.5.1.3. The extra components in the expanded File Save dialog.
In order to select folders other than those provided in the drop down list shown as area B in Figure 14-6, the File Save dialog must be expanded by clicking in the area labeled D. In the expanded form, the File Save dialog allows a user to select a new folder in which to save a file, to create new folders, and to add bookmark folders to the list provided in the area labeled C.
This section will explain the extra components of the File Save dialog which are provided when the dialog is expanded. Figure 14-7 shows these different areas and adds a label to each.
The different parts of each panel of the File Save dialog after it has been expanded have been shaded with boxes of different colors and labeled with a letter in Figure 14-7. Five of the labeled areas are the same as the areas in the dialog when it is in a compact form; these areas were explained above. The remaining areas are explained below:
- F - The 'relative root' selection area.
-
This area allows the user to select the starting folder from which to navigate the folder hierarchy. The navigation system only allows users to select sub-folders of the currently selected 'relative root' folder so the root folder selected in area F must contain the desired folder as a sub-folder.
The folders listed in this area include the standard folders provided by the system and a number of folders added, as bookmark folders, by the user. The standard folders provided by the system will vary for different machines and system administrators may have disabled access to certain areas. By default, the standard folders provided include the user's 'Home' folder, the user's 'Desktop' folder, a folder pointing to the root of the filesystem tree and folders for each of the removable storage devices attached to the computer. The user's home folder, on GNU and other UNIX like systems, this folder is usually known as ~ or ~user_account_name where the phrase user_account_name represents the account name used by the current user. This folder is often located at /home/user_account_name/ in the filesystem. The 'Desktop' folder is the folder which holds the files which are displayed in the background of the user's window. The 'Filesystem' folder is the top of the filesystem tree, which on GNU systems is also known as /. The list also presents peripheral or external devices. Below the standard folders, area F has a separator and the bookmark folders selected by the user. In Figure 14-7 the folder currentWork is a folder named by the user and added to the list of bookmark folders.
- G - The folder hierarchy area.
-
This area displays the folder hierarchy starting from the starting folder selected in area F and ending in the current folder, the folder whose contents are displayed in area I, while displaying all the folders between the two. This area changes dynamically as the user changes to new folders. In the case shown in Figure 14-7, the user has selected the 'Home' folder as the starting folder in area F and has not navigated to any sub-folders.
- H - The Folder Creation button.
-
This button allows the user to create a folder in the directory listed in the rightmost part of the file component area, area G. When this button is clicked, by placing the mouse pointer over the button and clicking with the primary mouse button, a new folder is added to the list in area I with a temporary name of 'Type name of New Folder' pre-selected and therefore ready to be edited into a new name.
- I - The folder content area.
-
This area displays the contents of the currently selected folder which is the rightmost folder shown in area G.
Not all of the sub-folders and files present in the folder area are shown.
Firstly, hidden folders and files, those that start with a leading period, are not displayed by default. These can be shown by placing the mouse pointer over area I, clicking with one of the secondary mouse buttons to raise the context menu, moving the pointer onto the menu entry, and clicking with the primary mouse button. This step will ensure that all the folders are displayed.
Secondly, the filtering rule defined in area L will limit the files displayed based on the characteristics of these files. By default, a filtering rule is applied which causes only those files present that have an extension commonly used for spreadsheet files. The rule can be changed to display all the files regardless of their extension, except possibly for the hidden files.
- J - The panel rearrangement handles.
-
These triple dots indicate that the mouse can be used to change the shape and size of the different areas in the dialog. These handles can be used by placing the mouse pointer above a handle, clicking and holding with the primary mouse button, then dragging the handle to a new position, and then releasing the mouse button.
- K - The bookmark folder list modification buttons.
-
These buttons will add or remove folders to or from the list of bookmark folders in area F. The button will add the folder currently selected in area G. The button will remove any bookmark folder that is selected in area F.
- L - The filter definition area.
-
This area contains a drop down menu with the different filters defined by the application. Gnumeric currently defines two filters. The first filters out all files that do not have an extension used by the spreadsheet formats supported by gnumeric. The second filter, labeled "All files", essentially disables any filtering operation, and lists all the files in the currently selected folder, except that files starting with a leading period are not shown.
The uses of the File Save dialog in its expanded form is explained below.
14.5.1.4. Changing the currently selected folder.
In order to save a file in a folder other than that provided by default, it is necessary to change the default folder. The note below explains briefly the notion of folders and the procedure further down explains how to change folders.
In order to understand how to change folders, it is first necessary to understand the system by which documents are stored. This system is called the 'filesystem'.
All documents are stored in a folder. Folders can contain files but can also contain other folders. Any folder therefore can contain several sub-folders, each of which may itself contain several sub-folders; the resulting structure is called a nested 'tree' with the original folder being the 'relative root' of that tree.
In GNU and UNIX systems, all of the files are stored in folders organized in a single, unified filesystem tree with a folder named '/' at the absolute root of the tree. Every file is accessible from this absolute root folder and, by default, this folder is provided as the choice named Filesystem with an icon of a disk drive in area F in the File Save dialog.
Navigating the directory tree from the single root folder would quickly become burdensome and the File Save dialog provides several other starting points in area F. These will be called, in this documentation, the 'relative root' folders since each of these will act as the root of the branching structure of sub-folders the relative root folder contains. Two relative root folders which are commonly provided are the 'Home' and 'Desktop' folders for the current user.
In a complex computer system, the absolute root folder may be hidden from the user and only 'relative roots' will be present. These should jointly provide some way to access all the areas where the user can save files.
The 'relative roots' are also necessary when several file systems are available to the user. This will be the case when filesystem on other machines are accessible over a network or when Gnumeric is running on operating systems whose filesystems are not unified, such as the proprietary operating systems sold by Microsoft in which each disk drive has its own root named, for example, C:\ or D:\.
Additional 'relative root' folders can be added as 'bookmark folders' by the users themselves. These bookmark folders can be used to access quickly folders which are commonly used. The bookmark folders are listed, in area F, under the thin horizontal separator line. The creation and deletion of these bookmark folders is explained below, in Section 14.5.1.6 ― Changing the list of bookmark folders. .
Changing folders involves selecting a 'relative root' folder, then navigating into the appropriate sub-folder. When the button is pressed, the file will be saved in the folder listed as the right most button in area G of Figure 14-7 which also means that the file will be saved alongside the folders and files listed in area I.
To select a new folder, one of the 'relative root' folders which contains the desired folder must first be selected and then the hierarchy must be navigated to find the desired folder. As explained below, a user can move around the hierarchy using as many changes as they need to choose the folder in which to save their Gnumeric file.
-
Select a 'relative-root' folder in area F.
The first step in choosing a new folder requires selecting, in area F, a 'relative root' folder which contains the desired folder. The new 'relative root' folder is chosen by placing the mouse pointer over the folder name and double clicking (click twice rapidly without moving the mouse) with the primary mouse button. This will change the leftmost button in area G and change the folders and files listed in area I.
-
Navigate the filesystem to reach the desired folder using area I.
The next step involves descending the folder tree to reach the desired folder. This requires double clicking the sub-folder of the 'relative root' folder which contains the desired folder and continuing through the whole hierarchy until the desired folder is reached. After each double click, the selected folder is added as the right most button in area G and the contents of the selected folder are shown in area I. Once the desired folder is reached, it must be opened in the same way, so that its contents are listed in area I and the file can then be saved into this folder by clicking on the button.
-
Navigating back up the folder tree using area G.
If the sub-folder selected in area I does not contain the branch of the folder tree leading to the desired folder, the buttons in area G can be used to jump further up the folder tree but only as far as the 'relative root' folder selected in area F. Area G provides a list of buttons with the names of all the folders between the 'relative root' listed in area F and the currently selected folder. By clicking on one of these buttons, that is by placing the mouse pointer over the button and clicking with the primary mouse button, the folder listed on the button will be opened in area I so that the selection process can restart from this branch.
The process of exploration of the folder tree can continue as long as the user wishes. If the user desires it is also possible to create new folders as is explained next.
14.5.1.5. Adding a folder.
Often the user wishes to save the Gnumeric workbook by creating a file in a folder which does not yet exist. A new folder can be added to the folder tree by clicking on the button, which is labeled as area H of Figure 14-7. The button can be clicked by placing the mouse pointer over the button and pressing the primary mouse button.
When the button is pressed, a folder will be added at the top of the list in area I, with its name, Type name of new folder already selected so that the user can simply start typing to give the folder a desired name. Once the name has been entered on the keyboard, typing the Return key (or the Enter key, depending on the keyboard) will change the folder name and open that folder. Area I will therefore be empty since the newly created folder has no contents.
There is no way to delete folders once they have been created, just as there is no way for Gnumeric to delete files it has created. Folders created by mistake must be deleted using a file browser such as Nautilus or using command line programs such as rm.
14.5.1.6. Changing the list of bookmark folders.
The list of 'relative root' folders shown in area F of Figure 14-7 may contain 'relative root' folders selected by the user. These folders are called 'bookmark folders' and are listed in area F below a thin horizontal separator line. For example, Figure 14-7 contains a folder named currentWork which is a bookmark folder selected by the user.
These bookmark folders can be added in two ways. A folder which is selected in area I can be added as a bookmark by clicking on the button in area K.
Alternatively, the folder can be dragged from area I into area K. The folder can be dragged by placing the mouse pointer over the folder name in area I, clicking and holding the primary mouse button, moving the mouse pointer to area F and releasing the mouse button. As the mouse pointer is moved from area I to area F, a small icon of the folder will move with the mouse pointer.
Any bookmark folder can also be removed from the 'relative root' folders presented in area F (or in the drop down list labeled B). A bookmark folder can be removed by clicking on the folder name in area F and then clicking on the in area K.
14.5.2. The file formats which Gnumeric can write.
Gnumeric can write files in several formats used by other programs. The details of these formats are provided in Section 14.2 ― File Formats and the name of each file type in the table below skips to the appropriate section of Section 14.2 ― File Formats. The creation of files which consist of structured text is described in Section 14.6 ― Exporting Text Files. The creation of PostScript and Portable Document Format (PDF) files is done through the printing mechanism and is described in Chapter 15 ― Printing.Gnumeric can also export text data or HTML and XHTML tables through the clipboard mechanism, as is explained in Section 5.7.4 ― Cut and Paste Between Gnumeric and Other Applications.
Most of these formats are provided by plugins, which are independent, configurable modules. If a format described below does not appear in the File Save dialog, this may be because the appropriate plugin has not been configured or started. This can be verified by examining the list of plugins which are currently running in the Plugin Manager dialog.
The Plugin Manager dialog lists the plugins which are currently in use and provides a way to start plugins which are currently disabled. The Plugin Manager can be started by selecting, in the menu, the menu item; see Section 13.4 ― Plugins for more information.
| Format | Extension |
|---|---|
| Gnumeric | .gnumeric / .gnm |
| Comma Separated Values | .csv |
| Data Interchange Format | .dif |
| HTML | .html / .htm |
| LaTeX | .tex |
| Microsoft Excel Old Binary | .xls |
| Microsoft Excel New Binary | .xls |
| Microsoft Excel 2003 XML | .xls |
| Microsoft Excel Office Open XML | .xlsx |
| OpenOffice.Org / StarOffice (OASIS ODF/IS26300) | .ods / .odt |
| OpenOffice.Org / StarOffice Old Format | .sxc / .stc |
| PostScript | .ps / .eps |
| Multiplan (SYLK) | .sylk / .slk |
| Tab Separated Values | .tsv / .tab |
| Text Formats | .txt / .text |
| TROFF | .me |
| XHTML | .xhtml / .html |
14.6. Exporting Text Files
Gnumeric can export worksheets to structured text files. To create a text file one chooses the item in the submenu of the menu. In the dialog, one specifies the file name, and selects the folder in which to save it, retaining the file format "Text export (configurable)". Upon clicking Save the Text Export druid appears which permits the configuration of file structure characteristics.
The steps involved in the text export druid are:
- Launch the Text export druid using, in the item in the submenu of the retaining the "Text export (configurable)" file format type.
- Select the worksheets to include in the exported file.
- Configure the order of the worksheets for the exported file.
- Go to the second panel.
- Select the line termination character.
- Select the value separating character or character sequence
- Select when values should be surrounded by a text indicating character.
- Select the character or sequence to use to indicate a text field.
- Configure the character encoding to use for the file.
- Select how to handle unknown characters.
- Select whether to preserve the format of the cell contents.
- Click on the button to export the file.
14.6.1. The Components of the Text Export Druid
The Text Export druid consists of two panels. The first panel allows the user to select the worksheets included in the export and their order. The second panel allows the user to configure the structuring elements, the line delimiting characters, value separating characters, text indicating characters, and file encoding.
- 14.6.1.1. The first panel of the Text Export Druid.
- 14.6.1.2. The second panel of the Text Export Druid.
14.6.1.1. The first panel of the Text Export Druid.
The first panel of the Text Export Druid allows users to set the file encoding, to determine the character sequences used to separate lines, configure the type of structuring being used and select the lines of the file to import.

The different components of the first panel of the Text Export druid with each component labeled with a callout.
The purpose of each labeled component in Figure 14-8 is explained below:
- 1 - The worksheet selection area.
-
This area allows the user to select the worksheets to be included in the file. By default, only the top most sheet will have its checkbox checked and be included in the export. The user can add sheets by clicking in their checkboxes to set the check marks.
- 2 - The worksheet selection and ordering buttons.
-
The top two buttons allows the user quickly to select or unselect all the worksheets to be included in the export file. The bottom two buttons allow the user to change the order of the worksheets in the file to be exported.
- 3 - The button area.
-
These three buttons allow the user to navigate the druid. The button will dismiss the dialog and return the user to the worksheet. The button is disable since this is the first panel of the druid. The button will dismiss the first panel and bring up the second panel of the druid.
14.6.1.2. The second panel of the Text Export Druid.
The second panel of the Text Export Druid allows users to select the line termination character, configure the value separating character, select the text indicating character and set the character encoding.
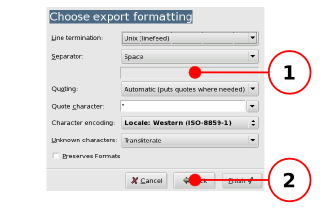
The different components of the second panel of the Text Export druid with each component labeled with a callout.
The purpose of each labeled component in Figure 14-9 is explained below:
- 1 - The export characteristic menu buttons.
-
These drop down menus provide to set the different configuration parameters for the exported file. The various menus are as follows.
.-
Line Delimiting Character-
This button allows the user to activate a drop down list from which to select the character used to indicate the end of a line and beginning of the next. The three commonly used alternatives are provided. See Section 14.4.1.2 ― Line break delimiters for more details.
-
Value Separating Character-
This button allows the user to select a character to use as a value separator. The "Custom" type will active the text entry area to allow the user to determine a particular character or character sequence to use to delimit data values. See Section 14.4.1.3 ― Data Structuring Strategies for more details.
-
Value Separating Character entry area-
This entry area allows the user to define explicitly the character or character sequence which should be used to separate each value field on every line. This area is only active if the "Custom" type has been selected from the list in the button above.
-
The Text Field Delimiter activity setting-
This button activates a list with three choices for the use of text field delimiters. Text fields can be delimited only where needed, meaning that the quote characters will only be used if the value contains the character used as a separator or a space. Alternatively the text field separators can be used around all values or never applied. See Section 14.4.1.3 ― Data Structuring Strategies for more details.
-
The Text Field Delimiter character entry area and list-
This area can be used as a text entry area to type the character to use to delimit text fields. Alternatively, three pre-selected characters, double quotes or single quotes, can be selected from the drop down list which appears by clicking on the downward pointing arrow to the right of the text field.
-
File encoding selection button-
This button allows the user to set the encoding scheme to use for the file. By default, Gnumeric selects the encoding scheme used by the locale of the user. See Section 14.4.1.1 ― Character Encodings for more details.
-
The unknown character handling setting button-
This button selects whether to escape or transliterate characters which Gnumeric does not recognize.
-
The format preservation checkbox-
This checkbox sets whether to preserve the number formats for formatted values.
-
- 2 - The button area.
-
These three buttons allow the user to navigate the druid. The button will dismiss the dialog and return the user to the worksheet. The button is disable since this is the first panel of the druid. The button will dismiss the druid and cause the file to be saved using the selected options.
14.7. Sending Files
Gnumeric can send files directly as attachments to an electronic mail (email) message, as long as Gnumeric is run in an environment where it can access an Email client.
14.8. Converting Files
Gnumeric can convert files automatically without needing user intervention. This allows a large number of files to be converted using a script. Gnumeric is distributed along with a program called ssconvert which is the program used to convert files automatically. All of the file formats supported by Gnumeric can be used except for the PostScript and PDF file formats which operate through the printing system.
This application is used, from the command line by specifying, any desired options, an input file and an output file. For example,
ssconvert myfile.xls myfile.gnumeric
The available import and export file formats which ssconvert can read can be listed using
ssconvert --list-importers
ssconvert --list-exporters
Like other GNU command line applications, ssconvert includes a manual page. This page can be accessed by typing:
man ssconvert
15. Printing
This chapter explains how to print spreadsheets, tables and plots from Gnumeric to a printer directly or into PostScript or PDF (both are page description languages).
- 15.1. Printing to a Printer or a File.
- 15.2. Page Setup.
- 15.3. Print Preview
15.1. Printing to a Printer or a File.
The Print dialog includes the most important options related to printing. More detailed options related to printing can be set in the Page Setup dialog, detailed in Section 15.2 ― Page Setup.. Press the to print out the workbook. Press the button to display the Print Preview.
The number of tabs and the content of some of the tabs of the Print dialog depends on the printer model you use. Some of the described tabs or options may not be available with your printer, especially when printing to a file.
- 15.1.1. Print General
- 15.1.2. Page Setup
- 15.1.3. Print Range
- 15.1.4. Print Job
- 15.1.5. Image Quality
- 15.1.6. Finishing
- 15.1.7. Advanced
15.1.1. Print General
Select the preferred printer in the upper half of the tab. Your default printer is already highlighted when you open the Printer dialog. Optionally select the number of copies and a page range in the lower half of the dialog. Click on to send the document to your printing system.
When printing to a file you may want to change the output name and folder before printing. You can choose between saving a PostScript or a PDF file.
15.1.2. Page Setup
In the tab you can choose several options concerning the layout or the paper. Choose how many sheets shall appear on one piece of paper, about two-sided printing, limit the printed pages by even or odd page numbers or the scale in the layout section. Select the paper type (e.g. preprinted) and the paper source and output tray in the paper section.
The preview in the lower part of the tab gives you a small hint of how your printed document will look like.
15.1.3. Print Range
The tab gives you the opportunity to limit the range of the printed workbook. You may choose between printing the whole workbook, only the selected or not the selected area or a defined range of worksheets.
15.1.4. Print Job
In the tab you may change the priority or add billing information to the print job. Also you can choose to add a cover page in front or after the printed worksheets. Finally you can decide whether your job should be printed right now or at a defined point in time.
Some options may be unavailable due to user restrictions. Ask your local administrator for further details.
15.1.5. Image Quality
In the tab you can select the resolution of the printed document depending on your printer. No more, no less.
15.2. Page Setup.
The Page Setup Dialog can be used to configure various options related to printing out a workbook. Click on to activate the Page Setup.
Remember that at any time you can click on the button to see what your document looks like with your selected options. See the Section 15.3 ― Print Preview
Normally the specified settings apply only to the current sheet. Select another sheet at the bottom of the Page Setup Dialog or select Apply to all sheets of this workbook. You can also save your adjustments by activating the save as default settings flag.
- 15.2.1. Page Setup Dialog - Page
- 15.2.2. Page Setup Dialog - Scale
- 15.2.3. Page Setup Dialog - Headers and Footers
- 15.2.4. Page Setup Dialog - Print Area
- 15.2.5. Page Setup Dialog - Sheet
15.2.1. Page Setup Dialog - Page
Change the paper type by clicking the button.
Select the preferred printer or choose Any Printer to see the formats supported by all printers. Pick a paper size and page orientation (portrait, landscape or reverse) to suit the best layout for your document.Specify the required margins of the page. Nothing will be printed inside these margins, not even page numbers. The margins will be measured in the same units (millimetres, points or inches) as the paper size. Change the unit in the paper and layout section to best fit your needs. You may also specify whether the page is centered horizontally and/or vertically on the printable part of the page.
15.2.2. Page Setup Dialog - Scale
Select the scale applied while printing. You can choose between no scaling, a fixed scaling or automatic scaling to fit the workbook to a defined number of paper sheets.
15.2.3. Page Setup Dialog - Headers and Footers
Select a predefined format for either the header or the footer. You can define an header or a footer by clicking the button next to the according drop-down field.
Headers and footers are divided into left, center and right area. Select the area you want to change. Insert a user-defined text or just select one or several of the given options. When selecting and/or you may choose the format by clicking on the arrow next to the symbol and click on the preferred option. Beside the according number, the number of total and the name of the according worksheet, you may also insert the name and/or . Finally you can select a defined to appear in the header/footer. Additionally there are a number of special opcodes for common options. These are:
- &[TAB]
-
Name of the worksheet.
- &[PAGE]
-
Page number in the printing.
- &[PAGES]
-
Total number of pages in the printout.
- &[DATE]
-
Current date in format dd-mmm-yyyy. The format can be changed by specifying the desired format in the opcode: &[DATE:yyyy/mm/dd].
- &[TIME]
-
Current time in format hh:mm. The format can be changed by specifying the desired format in the opcode: &[TIME:hh:mm:ss].
- &[FILE]
-
The basename of the file. For the file /home/jdoe/file.gnumeric, this opcode prints file.gnumeric.
- &[PATH]
-
The path of the file excluding the basename. For the file /home/jdoe/file.gnumeric, this opcode prints /home/jdoe/.
- &[CELL:$A$1]
-
The content of the cell $A$1 on the sheet being printed. Instead of $A$1 any other absolutely addressed cell may be used.
- &[CELL:A1]
-
The content of the top left cell on the current page. Instead of A1 any other relative cell address may be used. This relative address is interpreted with respect to the top left cell on the current page. Any repeating rows or columns are ignored.
- &[CELL:rep|A1]
-
The content of the top left cell on the current page. Instead of A1 any other relative cell address may be used. This relative address is interpreted with respect to the top left cell on the current page. Repeating rows or columns are not ignored. So if the top left cell is in a repeating row or column then the relative address is interpreted with respect to that cell.
You can choose the font in which the header and footer is printed by selecting a default header/footer font in the preferences (see in Section 13.2 ― General Preferences).
Double clicking on the header or footer preview will quickly allow you to customize that header or footer.
15.2.4. Page Setup Dialog - Print Area
You can select rows or columns to be printed on every page of the output. This is commonly used for printing column or row names. To enable this, enter the range of cells to be repeated in Rows to repeat... or Columns to repeat... field. Instead of entering them manually, you can also select columns or rows to be repeated using the mouse.
Note that the rows and columns must be entered as ranges. That is, if you want to have first row repeated, you must enter 1:1, not just 1. Similarly, to have column A repeated, you must enter A:A.
15.2.5. Page Setup Dialog - Sheet
Select Grid lines to print the cell grid lines with your document. Unselect the button to hide the grid lines from your print output.
Select Black and white to convert the colours in your document to a greyscale range.
Select Do not print with all sheets if you want to avoid printing this sheet whenever you choose to print all sheets. If this item is checked then this sheet will only be printed as the active sheet or as part of a range of sheets. This is useful if you have a non-hidden sheet that contains only auxillary information and should normally not be printed.
Select Row and column headings to print the row and column headings (1,2,3,... and A,B,C,...).
Select Styles with no content to ensure cells with style changes will be printed, even if they are empty. For example, if you have a number of cells with the background color changed but no data in them, you can select this option to ensure they are in the printed output.
The Errors selection box allows you to choose how to print error values:
- Print as displayed
-
Every error value is printed just as shown on the worksheet.
- Print as spaces
-
No error values are printed.
- Print as dashes
-
Every error value is replaced by two m-dashes (separated by a thin space): "— —".
- Print as NA
-
Every error value is printed as an #N/A error.
Finally you can decide about the direction in which the workbook will be printed (Down, then right or Right, then down).
15.3. Print Preview
The Print Preview Dialog is used to display what the printed output will look like. The Print Preview dialog can be used to check whether you have the desired formatting and layout before you print out the workbook. Evince is set up to be the default viewer.
15.3.1. Customizing the preview application
You may change the default preview application by editing your presets for GTK. Open the file .gtkrc-your GTK version and add a line in the format gtk-print-preview-command="command to your preferred viewer".
Please make sure you have only one line defining your preview application.
It is strongly recommended to use Evince as the default viewer. A convincing argument is that Evince deletes the preview file after closing the viewer.
16. Getting More Help
This chapter describes other sources of help which are available to users including the Gnumeric web site, the mailing list, and the internet relay chat (IRC) discussion channel.
- 16.1. Sources of Help
- 16.2. Web Resources
- 16.3. Related Manuals
- 16.4. The Mailing List
- 16.5. Internet Chat (IRC)
16.1. Sources of Help
This manual is the most complete source of explanation for Gnumeric and attempts to describe as much of the program as possible. However, this manual cannot answer all the possible questions readers may have: the manual is not yet finished and there are many situations which cannot be explained through a manual. Other sources of information which might be helpful to Gnumeric users are presented below.
Several of the sources of information below involve talking directly with the people who have created Gnumeric. These people are volunteers who have spend several years working on the program to make it useful. They will all be glad to help you but only if they decide they want to. They are all busy and only volunteer on this project. You can take several steps to make these people want to help you.
First of all, try to help yourself by reading the existing documents. If you have read the documents, others will be much more likely to want to answer any questions that remain. Secondly, be polite by introducing yourself, thanking developers for their hard work and asking your questions nicely. Please be aware that the developers all respect each other and their users so therefore, while their answers may appear brisk or discourteous, they are simply trying to be efficient and save time by being curt. Please assume they respect you and want to help you, after all they have written a program for you to use.
Steps for getting help.
-
Read the Manual:
First, please look carefully through this manual to see if you can answer your own question. This can be hard and requires careful thinking but will teach you the most.
-
Read the Web Site:
Second, look at the Gnumeric web site, look on the world wide web for explanations using other spreadsheets or look for a book on how to use another spreadsheet. Section 16.2 ― Web Resources explains how to access and find information on the web site.
-
Read other Spreadsheet Tutorials:
Another useful source of help is the literature written for other spreadsheets. Gnumeric is quite similar to a number of other spreadsheets and often books, web sites, tutorials and other documents which describe how to use other spreadsheets can help users understand how to use Gnumeric. Section 16.3 ― Related Manuals describes other spreadsheets for which usage manuals may provide useful information.
-
Send email to the Gnumeric List:
The Gnumeric project maintains an email mailing list which is a way for people to send email to all the core developers. Section 16.4 ― The Mailing List explains how to send email to the gnumeric list and how to read past messages including questions and answers which may be helpful.
-
Join the Chat Discussion:
The Gnumeric project also uses an Internet Relay Chat (IRC) channel, also known as a `discussion room', in which developers talk to each other, and to anyone else, about the program. Section 16.5 ― Internet Chat (IRC) explains how to join this discussion.
16.2. Web Resources
The Gnumeric project maintains a web site with explanations, links and other useful information to learn about and use this spreadsheet.
- 16.2.1. The Gnumeric Web Site
16.2.1. The Gnumeric Web Site
The Gnumeric web site can be accessed by clicking on this link. Alternatively, it may be necessary to enter the address directly into a web browser. The Gnumeric project page address is:
http://www.gnome.org/projects/gnumeric/
16.3. Related Manuals
Gnumeric strives to mimic the behaviour of other spreadsheets so books which explain how to use these other spreadsheets will probably be useful to help understand Gnumeric.
The OpenOffice.org spreadsheet named Calc is another popular and highly functional spreadsheet which provides users with the freedoms provided by Gnumeric including the freedom to access and use the source code of the program itself. The documentation for Calc may also help explain how to use Gnumeric and can be accessed through the OpenOffice.org web site at http://www.openoffice.org/.
The manuals for other spreadsheets, even those that restrict users freedoms in several ways, may help to explain how to use Gnumeric. Gnumeric attempts explicitly to behave in a manner understandable to users of the Microsoft Excel spreadsheet. Because Excel has a very large number of users, many books have been written explaining how to use that spreadsheet. Any local bookstore should have at least a few of these books which may help answer any questions.
16.4. The Mailing List
The Gnumeric project maintains a mailing list which is a system by which people can send one email which gets distributed to everyone who has signed up to read these emails. Please understand that this list is used for serious discussions about developing this spreadsheet further. Questions from users are generally answered when posted to this list but simple questions which are answered in the manual may generate the simple answer, "Please read the manual." Also, developers volunteer any time they take to answer your questions so please be polite.
The best way to use this resource is first to read the archives for the past few months to see if any of the subjects look similar to the issue which interests you. It may be that your question has just been asked by someone else and a good answer has been posted. To access the archives, use a web browser to go to the mailing list web page at http://www.gnome.org/ and then ...
If none of the emails recently posted to the mailing list address your issue, if you would like clarification to an earlier answer, or if you simply want to thank the developers, you are welcome to send an email of your own to the list. This simply requires writing an email and sending it to
gnumeric-list@gnome.org
After you have sent your email, there may be an initial delay while the moderator of the list, a person who acts as editor, reviews your email to see if it is relevant to the discussion. This step is required to limit the junk email that gets sent out to everyone.
Very rarely an email might automatically be discarded if it appeared to be a mass junk mailing. If, after a few days, your email does not appear in the archives and you don't get any response, then re-send your email to the list omitting any signatures or other material that might appear to be commercial solicitation. A simple, text message is the least likely to be discarded by these automatic tools.
16.5. Internet Chat (IRC)
The GNOME and GIMP projects maintain a series of servers to provide a world wide network enabling an Internet Relay Chat (IRC) system for discussion on issues related to those projects including a discussion channel dedicated to Gnumeric. This is a system by which people can communicate directly with each other by typing lines into an IRC client which are then broadcast to everyone listening in a particular channel. Unfortunately this manual cannot provide a full explanation for how to obtain, install and use an IRC client. There are a number of such programs available, many of which provide users all the freedoms which Gnumeric provides and instructions for these can be obtained from the world wide web. More information and access to such software can easily be obtained by running a search in any world wide web search engine for "IRC" and "client" and the name of the operating system of the machine which will run the software.
The Gnumeric IRC discussion channel is named #gnumeric (although the number symbol, #, may not be needed) and is hosted on the series of servers called GIMPnet. The best way to connect to GIMPnet is using the IRC server irc.gimp.org. That hostname points to a variety of different servers in the United States. If you live elsewhere, after you are connected you can use the chat command /links to find a server which is closer on the internet to your location.
If you decide to join the discussion, please be polite, post a question or comment and be prepared to wait a little bit for someone to address you. Several of the developers are permanently connected to the channel and check every half hour or so to see if anyone has asked a question but are working on something else in the meantime. Your question may be answered right away but asking questions using the mailing list may prove to be more efficient since it would not require paying attention to the IRC channel discussion, even if it ultimately requires longer to obtain an answer.
17. Reporting a Problem
This chapter explains how to report a problem with Gnumeric so that the problem can be fixed. The same procedure can be used to file a report requesting an enhancement or a new feature.
- 17.1. Overview
- 17.2. Defining the error
- 17.3. Opening an account
- 17.4. Filing a report
17.1. Overview
Gnumeric is a complex computer program and therefore necessarily contains some mistakes. The Gnumeric team is keenly interested in finding these errors and correcting them. Suggestions for improvement are also welcome and can be submitted in the same fashion as an error report.
Please, help us to fix any errors by telling us about them.
Reports of problems with Gnumeric provide the project with a way of making sure that the mistake is eventually fixed. Often the mistake is obvious and a fix can be made immediately to be included in the very next release of Gnumeric. Occasionally, the mistake is more complex and the problem may take a while to be resolved. In these cases, the report provides a way to remind the developers that the problem still exists.
Mistakes in programs are often called "bugs" after one of the earliest errors in an old machine which was actually caused by an insect entering the machine and preventing a switch from closing.
The Gnumeric project uses a world wide web system called GitLab to collect reports of program errors and then to track these errors until they are finally fixed. The system was developed as part of the Mozilla web browser project, which explains the origin of the strange name.
The process of submitting the report of a problem or of a suggested enhancement is quite simple and can be completed in just a few steps. The process begins with obtaining a good understanding of the problem to be able to provide a detailed statement explaining the problem exactly. Next, the user must open an account with the GNOME project's GitLab system. Finally, the user must submit the statement of the problem, ideally, along with some information about the computer setup being used by the person experiencing the problem.
The explanation given below should be sufficient to file a report. For more detailed instructions, the main page of GNOME's GitLab can be found at https://gitlab.gnome.org/GNOME and instructions can be found at https://wiki.gnome.org/Community/GettingInTouch/BugReportingGuidelines.
17.2. Defining the error
The most critical step is understanding the error as well as possible. This requires knowing clearly what was happening before the error occurred, what specifically caused the error to occur, what the error condition is and what happened as a consequence of the error.
The most helpful situation to enable the developers to find and correct the error is to come up with a sequence of steps that generate the error. If the error can be repeated, it can almost always be corrected. The most helpful error reports include a small recipe that can cause the error to occur.
17.3. Opening an account
The first time a user uses Gitlab, they must create an account. This account is needed to allow users to be informed of the status of the bug as it is tracked by the system from submission to resolution. The only requirement for opening a Gitlab account is the possession of a valid email address through which the user can receive a password.
- 17.3.1. Creating a new account
- 17.3.2. Logging into the account
17.3.1. Creating a new account
Users of Gitlab are automatically redirected to a login page, unless they have previously logged into the system and accepted a 'cookie' with which they identify themselves. The login page has a link called "Create a new account" which will direct users to the account creation page.
Alternatively, by clicking on this link, users can follow a shortcut directly to the account creation page.
Creating a new account is very simple. The account creation page has two fields. In the first, a valid email account must be given. The second asks for a name by which the user wishes to be known. After a user fills out these two fields, clicking on the button labeled "Create Account" will cause a new account to be created and an email sent to the address given in the email field. The email will contain the password used to identify this user.
17.3.2. Logging into the account
After creating an account, users can visit the bug entry page for Gnumeric. Here users are asked to login with their email address and password. After logging in, GitLab will present a page to add a bug report.
A user who accepts cookies from gitlab.gnome.org will only have to give a password the first time they visit GNOME's GitLab. During all future visits, GNOME will recognize the cookie and thereby identify the user.
17.4. Filing a report
In order to file a report of a problem with Gnumeric, a GitLab account is necessary. Please see the previous section, Section 17.3 ― Opening an account, for an explanation of how to open an account.
The Gnumeric bug entry page consists of several fields many of which must be filled out to provide a useful bug report. The most important of these will be the "Bug Description" which contains both the brief "Summary" field which acts like an email subject line and the detailed description field "Step to reproduce the bug" which should be used to give a more complete explanation of the problem and, ideally, to describe step by step how to reproduce the bug. The only other field which is required is the "Component" field which can be set to "General" and left to the developers to define more specifically. The remaining fields can be helpful, since they provide extra information which may help resolve the problem, but are not necessary. After filling out these three fields, a user can, if they desire, simply skip to the bottom and press the button.
- 17.4.1. Accessing the GNOME project's GitLab
- 17.4.2. The Bug Description
- 17.4.3. Product and Component
- 17.4.4. The Severity and Priority of the Problem
- 17.4.5. The Version of Gnumeric and GNOME
- 17.4.6. The Type of Operating System and Distribution
- 17.4.7. Other fields and keywords
- 17.4.8. Submitting the report
- 17.4.9. Bookmarking a template
17.4.1. Accessing the GNOME project's GitLab
There are several ways to file a bug report through GitLab.
One of the entries in the menu is called . This menu entry should cause a browser window to launch and open GitLab to the Gnumeric page.
Alternatively, users can click on this link to access the Gnumeric page in Gitlab.
If neither of those shortcuts work, the user must use a web browser to access the following location:
https://gitlab.gnome.org/GNOME/gnumeric/-/issues/new
The user may be asked to login, by giving their account name and their password, when they begin their browser session with GitLab. See Section 17.3.2 ― Logging into the account for an explanation of how to login to GitLab.
17.4.2. The Bug Description
A useful error report will include a subject that describes the error concisely, has a brief introduction which explains in greater detail what happened and, ideally, has a small recipe that leads to the error being repeated.
The summary field, like the subject of an email message, briefly describes the problem. For example, a useful error report might have a summary "Gnumeric crashes when saving a file".
The field titled "Steps to reproduce the bug" should contain a slightly expanded version of the summary giving an overview of the problem and then give a step-by-step example of how to reproduce the problem. For example, this field could look like the following:
This report describes an error which causes Gnumeric to crash during the use of the file save dialog. 1) Start a new Gnumeric 2) In Cell A1 type "hello" 3) From the "File" menu, select "Save As" => The "Save As dialog" opens up 4) In the file name box, type "my_spreadsheet.gnumeric" 5) Click on the "Save" button => I expected the file to be saved, and to be able to keep working but instead Gnumeric disappeared and the file was never saved. thanks, a user
17.4.3. Product and Component
The Product should be set to Gnumeric since the GNOME version of GitLab is used for all the different programs in the project.
The Component describes the part of Gnumeric that causes the problem. This may not be obvious so, unless one of the other entries clearly matches, the component should be set to "General". The possible components for Gnumeric are as follows.
| Component | Explanation |
|---|---|
| Analytics | Problems with calculations and other mathematics. |
| Charting | Problems with graphical plots of worksheet data. |
| Compilation | Problems encountered during source code compilation. |
| Database plugin | Problems when using a database from Gnumeric. |
| Documentation | Problems with this manual, with the explanations of functions, or with any other explanations. |
| General | The Default. Use this when none of the other categories apply. |
| GUI | Problems with the graphical user interface. |
| GUI Expression Entry Widget | Problems while entering or editing cell contents. |
| import/export Applix | Problems opening or saving a file to the file format used by the Applix spreadsheet. |
| import/export HTML | Problems opening or saving a file to the HTML or LaTeX file formats. |
| import/export MS Excel (tm) | Problems opening or saving a file to any of the various file formats used by the Microsoft Excel spreadsheet. |
| import/export OOo / OASIS | Problems opening or saving a file to the OASIS file format used by OpenOffice.Org Calc or Star Office Calc. |
| import/export Text | Problems opening or saving a file to a text file format including tab, comma and space delimited files. |
| Installation | Problems encountered during Gnumeric installation. |
| Main System | This component is no longer used. |
| Printing | Problems encountered when printing a worksheet. |
| Sheet Objects | Problems with any images, widgets, or drawing elements added to a worksheet. |
17.4.4. The Severity and Priority of the Problem
The severity level indicates the seriousness of the problem and the priority level indicates the desire of the developers to address the bug. These fields are used mostly by the developers and should both be left as "normal" unless the user has a good reason to change them.
There are two cases when the user should change the severity of the report. In the first case, if the user has a problem which causes Gnumeric to crash (to suddenly disappear or stop working) or a problem in which data is lost, the severity should be set to "critical". In the second case, if the user has a report about a desired feature, the severity should be set to "enhancement" so the developers will know right away that the desired functionality has not yet been added to the program.
The problem severity levels are explained below.
| Severity Level | Explanation |
|---|---|
| blocker | The level used to indicate a problem which must be fixed before any next release. |
| critical | The level used to indicate a very important problem such as a program crash or loss of data. |
| major | The level used to indicate a severe problem but one that does not cause a crash or loss of data. |
| normal | The level to use by default and used for the majority of reports. |
| minor | The level used for problems which do not affect the functioning of the program. |
| trivial | The level used to report typos, aesthetic, and other very small problems. |
| enhancement | These are reports which are requests for future improvements of the program. |
The priority level should be left at the "normal" level since this is a field used by the developers themselves.
17.4.5. The Version of Gnumeric and GNOME
The version field is used to indicate the version of Gnumeric which was used when the problem occurred. If the problem occurs with several versions, the most recent version number should be used. The version number can be obtained by opening the "About Gnumeric" dialog using the menu and the menu item.
The "GIT" version refers to a version which the user has recently obtained from the Git revision control repository provided by the GNOME project.
The "Other version details" text box can be used to describe any unusual characteristics of the program such as plugins which were added or other uncommon modifications.
If Gnumeric is being used with a GNOME desktop, the version of GNOME being used can be entered in the "Gnome Version" field.
17.4.6. The Type of Operating System and Distribution
The "Operating System" field can be used to describe the underlying operating system being used to run the Gnumeric program. Please note, that if the program is run in an artificial environment such as a virtual machine or a Cygwin setup, this should be indicated in the next field.
The "Distribution/Version" field should be used to add detail to the operating system described earlier.
17.4.7. Other fields and keywords
These fields are used by advanced users to better sort through all the reports. The "Keywords" field is used to relate the reports to each other and the "CC" field is used by those who are interested to add themselves to those who are notified when changes are made to the report.
17.4.8. Submitting the report
In order to submit the bug report into GitLab, once all of the important fields have been submitted, simply click on the button.
Once the bug is committed, a bug report number for this bug will be assigned, and email will be sent either the project maintainer or to one of the other developers which deal specifically with that component of the program. When others take an interest in the bug and add comments or solutions, email will be sent out to the user to inform them of the status of the bug until it is either dismissed or resolved. Bugs can be dismissed if they describe a behaviour that is expected or if they are not deemed important enough to fix.
A user can choose not to be notified when changes to reports are submitted. The user preference page can be accessed here at the following URL.
https://gitlab.gnome.org/profile/notifications
17.4.9. Bookmarking a template
A version of the bug entry page with most of the fields already filled out can be saved as a link and bookmarked for future use. This ability is only of use for developers or for users who have found a large number of bugs in one particular component of Gnumeric.
To use this shortcut, first open a new bug report, then fill out only the fields that will apply to all the future bugs being reported and then click on the button labelled "Bookmark these values". GitLab will then construct a template and will provide a link which can be saved for future use just as any other page on the web can be saved as a bookmark. To use these values, simply clicking on the bookmark will open the Gnumeric page of GitLab with the common fields already filled out.
18. Extending Gnumeric
This chapter explains how to go about extending Gnumeric to provide extra functionality. Because Gnumeric is Free Software this is quite easy to do.
18.1. The Approaches to Extending Gnumeric
There are several ways that Gnumeric can be extended to add functionality.
18.3. Programming Gnumeric using Python
A powerful way to access and manipulate data in Gnumeric involves using the Python programming language. As Gnumeric develops from version 1.2, the scripting methods will become increasingly powerful. Since Gnumeric is free software, you could extend it directly using the source code and adding C language functions to the code. Python offers a higher level abstraction through which to interact with the spreadsheet.
Python and Gnumeric can be used in several ways. This section will describe how to obtain Gnumeric, install it and get things configured correctly for access with Python. If you already have the pieces in place, you can skip the section Section 18.3.1 ― Installing and Building Gnumeric for Python.
This section was written by Charles Twardy. It owes a great deal to the nice guide Travis Whitton wrote: Python/Gnumeric guide for the old API in Gnumeric 1.0. Jon Käre Hellan contributed most of the code to enable Python in Gnumeric and wrote the file python-gnumeric.txt in the source tree. Nathan Hurst provided the idea and support.
The Python API, that is the list of methods available in Python, is still experimental and may change!
For further information, the web page maintained by Jon Käre Hellan's has some python plugins and other useful information. That page can be found through this link. The main Gnumeric page may also have useful information.
If you need help online, you may want to check out:
- The Gnumeric Function-Writer's Guide. Until I write one for Python, you'll have to settle for doc/developer/writing-functions.sgml in the Gnumeric source tree.
- The files that actually define the Python interface. In particular, plugins/python-loader/py-gnumeric.c has good comments at the beginning.
- The instructions on how to use GNOME Git can be found here.
- The gnumeric discussion list: <gnumeric-list@gnome.org>
- The IRC channel #gnumeric on the GIMPnet server. Right now, the project leader is Jody Goldberg (jody) and the Debianizer is: J.H.M. Dassen (jhm). Jody, Jon K. Hellan, and Zbigniew Chyla appear prominently in the Python ChangeLog.
- 18.3.1. Installing and Building Gnumeric for Python
- 18.3.2. The Python Console
- 18.3.3. Using the built-in Python functions
- 18.3.4. Writing your own Python functions
- 18.3.5. Upgrading
- 18.3.6. Fancy tricks
- 18.3.7. Features wanted, and Questions
18.3.1. Installing and Building Gnumeric for Python
This section describes how to obtain the Gnumeric source code, configure it for Python and build it. This section will eventually be removed as Python becomes supported by default.
- 18.3.1.1. Preliminaries
- 18.3.1.2. In the Beginning (Installing and Building)
18.3.1.1. Preliminaries
I'm going to define some variables here so that you can insert the appropriate command or item for your system when they occur. I'll prefix them all with '$'.
-
$root: Do whatever you do to become
root. The usual options are:
- su - and hit Enter
- sudo
- fakeroot (works in some situations, but not all)
-
$version: Whatever your current
Gnumeric version is. Some examples:
- 1.4.20
- 1.6.20
- 1.7.90
18.3.1.2. In the Beginning (Installing and Building)
You need to get Python and Gnumeric, and the Python plugin for Gnumeric. You can get the binaries, the packaged source, or the developing edge sources from Git.
- 18.3.1.2.1. Getting the binaries (Debian)
- 18.3.1.2.2. Getting and building the current Debianized source
- 18.3.1.2.3. Getting and building the source from Git
18.3.1.2.1. Getting the binaries (Debian)
I've only tested this on sid (unstable). The version you get from stable (woody) may not act quite the same.
-
$root apt-get install gnumeric gnumeric-python python
18.3.1.2.2. Getting and building the current Debianized source
If you have Debian, and don't need the bleeding edge, this is by far the easiest way to get and build the source.
-
Change to a directory where you want to hang the source directory.
-
$root apt-get build-dep gnumeric
-
apt-get source gnumeric
-
cd gnumeric-$version
-
debian/rules build
-
To make the .deb packages: $root ./debian/rules binary
-
To install those .deb packages:
-
cd .. to change to that directory.
-
$root dpkg -i gnum*deb (presuming you don't have other .deb packages beginning with "gnum" lying around here).
-
-
You may or may not want to remove those .deb files now: $root rm gnum*deb
18.3.1.2.3. Getting and building the source from Git
Remember that this is the developing edge. Things may not work. Generally don't do this unless you are subscribed to the mail list and possibly also on the IRC channel.
You will need a few things for this to work at all:
gnome-common
libgsf (see below)
-
pygtk2 (On Debian, make sure to get python-gtk2 and python-gtk2-dev)
gnumeric (see below, obviously)
And although the following will build in the main build space, it's probably better to build in a temporary space. But I can't be bothered to learn how to fiddle the build pathways.
-
Change to a directory where you want to hang the source directory for Gnumeric and a few other GNOME things.
-
Getting and building libgsf:
-
git clone git://git.gnome.org/libgsf
-
cd libgsf
-
Red Hat: ./autogen.sh
-
Debian: ./autogen.sh --prefix=/usr --with-gconf-schema-file-dir=/etc/gconf/schemas
-
make
-
$root make install
-
If you find that this didn't work, try make clean and then repeat from the autogen step.
-
-
Getting and building libgal No longer necessary! (13 June 2003)
-
Getting and building goffice:
-
git clone git://git.gnome.org/goffice
-
cd goffice
-
Red Hat: ./autogen.sh
-
Debian: ./autogen.sh --prefix=/usr --with-gconf-schema-file-dir=/etc/gconf/schemas
-
make
-
$root make install
-
If you find that this didn't work, try make clean and then repeat from the autogen step.
-
-
Getting and building gnumeric:
git clone git://git.gnome.org/gnumeric gnumeric-head
cd gnumeric-head
Red Hat: ./autogen.sh and wait while it compiles
Debian: ./autogen.sh --prefix=/usr --with-gconf-schema-file-dir=/etc/gconf/schemas
make
Optional: $root make install
If you find that this didn't work, try make clean and then repeat from the autogen step. For example, sometimes I've had it not create the python-loader.
OK, you should now have gnumeric! Test it! If you installed the Debianized version via apt-get, or did "make install", it should be installed to /usr/bin (or /usr/local/bin on Red Hat?) and you can just type gnumeric. Otherwise you will find it in gnumeric-head/src/ and you will have to run it from there.
18.3.2. The Python Console
There is an interactive Python console available from inside Gnumeric. This is a good place to explore things, and if the console is expanded, will be a nice place for scripting. In the meantime, what I have called "Spellbooks" below are much more useful, but are fixed plugins as of Gnumeric startup. So right now I putter in the console as I develop plugin literal in the form of spellbooks. After 1.2.0, Gnumeric will be working on its scripting API, so the two approaches may merge. Or not.
- 18.3.2.1. Enabling the Python Console
- 18.3.2.2. Playing with the Python console
- 18.3.2.3. More fun with the Python console
18.3.2.1. Enabling the Python Console
You can run a Python interpreter from inside Gnumeric, but you have to turn it on. To do this you simply uncomment a line in python-loader/plugins.xml. Normally, that file lives in /usr/lib/gnumeric/$version/plugins/python-loader/, or perhaps /usr/local/lib... on Red Hat. I used to suggest making a local but you should probably make a local copy, but that was pain for little gain. So:
-
gnumeric --version to make sure you get the right version name for the following. (You'll have to do this for every new version of Gnumeric!)
-
cd ~/.gnumeric/ $version /plugins/
-
Edit python-loader/plugin.xml.
-
Uncomment the five lines starting with ui-console-menu service near the bottom (remove the "<!--" and "-->" tags around the <service...> and </service> tags.
-
Save the file.
-
Start gnumeric (same version).
-
Select from the the .
-
Enjoy!
18.3.2.2. Playing with the Python console
At the top there is a drop-down menu . Right now your only choice will be . After you evaluate functions from other plugins, those environments will become available too (JK says this is called lazy loading). But I'll assume you are using Default. (The only real difference is that you have to import Gnumeric first, and you can't see your plugin functions.)
(Note: older releases required you to type print dir() instead of just dir(). Fixed in cvs 16 June 2003, and certainly in 1.1.20 and higher.
Let's start by taking a look at the environment.
>>> import 1Gnumeric >>> dir() ['Gnumeric', '__builtins__', '__doc__', '__name__'] >>> dir(Gnumeric) ['Boolean', 'CellPos', 'FALSE', 'GnumericError', 'GnumericErrorDIV0', 'GnumericErrorNA', 'GnumericErrorNAME', 'GnumericErrorNULL', 'GnumericErrorNUM', 'GnumericErrorRECALC', 'GnumericErrorREF', 'GnumericErrorVALUE', 'MStyle', 'Range', 'TRUE', '__doc__', '__name__', 2'functions', 'plugin_info', 'workbook_new', 'workbooks']
'Gnumeric' is a module that exists only within Gnumeric, and which defines the Gnumeric Python API.
Gnumeric.functions is the list of all the Gnumeric functions you would see in the function browser. You cannot yet do dir(Gnumeric.functions) but maybe someone will bind that soon.
RangeRef is not listed. That seems to limit us, though later in the tutorial we'll see how to use regular functions to get inside RangeRefs.
So do some exploring. First, let's poke around to figure out how to use CellPos.
# I wonder how to use CellPos (I've glanced at the source, but...)
>>> dir(Gnumeric.CellPos) # shows nothing useful
>>> Gnumeric.CellPos()
TypeError: CellPos() takes exactly 2 arguments (0 given)
>>> Gnumeric.CellPos("a1","a2")
TypeError: an integer is required. # Right.
>>> a=Gnumeric.CellPos(1,2) # It worked!
>>> a
<CellPos object at 0x106b6eb8> # Yeah, I know...
>>> dir(a)
['get_tuple']
>>> a.get_tuple()
(1,2) # Cool. That's (col,row)
>>> str(a) # Super cool.
'B3' # JK hasn't implemented this for tuples yet
Similarly, we can explore Gnumeric.Range:
>>> r = Gnumeric.Range((1,2),(3,4))
TypeError: Range() argument 1 must be CellPos, not tuple
>>> r = Gnumeric.Range(a,a)
>>> r
<Range object at 0x1071d888>
>>> dir(r)
['get_tuple']
>>> r.get_tuple()
(3, 7, 3, 7)
If you evaluate in the context of a plugin (rather than in Default), then dir(Gnumeric.plugin_info) will reveal some simple informational functions you can call for the local plugin(s).
Note: obviously I don't really know what I'm doing, or I wouldn't be poking around like this.
18.3.2.3. More fun with the Python console
Jon K. Hellan writes, "Here are some more things you can do from the console:"
# Get a workbook
>>> wb=Gnumeric.workbooks()[0]
>>> wb
<Workbook object at 0x862a490>
>>> dir(wb)
>>> ['gui_add', 'sheet_add', 'sheets']
# Get a sheet
>>> s=wb.sheets()[0]
>>> s
<Sheet object at 0x863e8d0>
>>> dir(s)
['cell_fetch', 'get_extent', 'get_name_unquoted', 'rename',
'style_apply_range', 'style_get', 'style_set_pos', 'style_set_range']
# Get a cell. s.cell_fetch(0,0) and s[0,0] are synonyms. First
# coordinate is columns, i.e. s[1,0] is B1.
>>> c=s[0,0]
>>> c
<Cell object at 0x863d810>
>>> dir(c)
['get_entered_text', 'get_mstyle', 'get_rendered_text', 'get_value',
'get_value_as_string', 'set_text']
# Change the cell - it changes in the grid
>>> c.set_text('foo')
# Retrieve the cell - both ways.
>>> c.get_value()
foo
>>> s.cell_fetch(0,0).get_value()
foo
Very, very nice. Note, after setting a value, it won't show up until that cell is redrawn. That will happen automatically with plugin functions, but in the console, you may have to click on the cell.
18.3.3. Using the built-in Python functions
To enable the Python-loader and Python plugins:
-
Select the menu and the menuitem.
-
Select "Python plugin loader" and "Python functions". Restart Gnumeric.
The quickest way to test whether you now have Python functions is to type =py_capwords("fred flintstone") in the first cell. After you hit <Enter>, you should see "Fred Flintstone".
You can also click on the functions button, and scroll down to the "Python" category. Select that. You should see at least two functions defined: PY_CAPWORDS and PY_PRINTF. They're not very useful, but they prove you've got the plugins. Test them either via the GUI or by typing into the cell.
I'll presume they worked.
18.3.4. Writing your own Python functions
To scribe new magic you must write your spells in places where Gnumeric will find them. That place is in folders under: ~/.gnumeric/<version>/plugins/ Each folder under here is one "spellbook" of new plugin functions. You may put all your spells in one spellbook, or group them neatly depending on your tastes. Each spellbook must have two files. We'll create a spellbook called "myfuncs". A pedestrian name for pedestrian spells. When I have more skill, perhaps I'll make some with better names. Several suggest themselves:
- Transformations: of obvious value for a spreadsheet
- Illusions: statistical functions, clearly
- Charms: presentation graphics
- Necromancy: file repair and missing values?
- Divination: data mining!
- 18.3.4.1. Prepare the spellbook
- 18.3.4.2. Writing new spells
- 18.3.4.3. Do it yourself (mostly)
- 18.3.4.4. More help
- 18.3.4.5. Program Listings
18.3.4.1. Prepare the spellbook
In many ways it would be easier to start by copying the py_func spellbook to your local .gnumeric folder, and just adding a function to that. But in general it will be more useful to be able to write your own separate spellbooks, so here we go.
-
Make the folder: First we make the folders and get into the right one. As noted above, we'll call our folder (spellbook) myfuncs.
-
If they don't already exist:
mkdir ~/.gnumeric
mkdir ~/.gnumeric/<version>
mkdir ~/.gnumeric/<version>/plugins/myfuncs/
cd ~/.gnumeric/<version>/plugins/myfuncs/
-
-
Make the files: A spellbook has two files. The first is the python file with the functions. The second is the XML file "plugin.xml". The XML file holds that master spells that tell Gnumeric what functions we've defined, and what the name of the python file is, and one other important item. We'll create these as blank files.
touch my-func.py
touch plugin.xml
-
Write the master spells The good news is that you only need to do this once per spellbook. After that you just add spells to it.
Your XML file must tell Gnumeric about your plugin. Here is a simple template. (If you want to learn about internationalization, see the example in the system's py-func spellbook.) Open up plugin.xml and insert the following lines:
<?xml version="1.0"?> <plugin id="Gnumeric_MyFuncPlugin"> <information> <name>Other Python functions from HOWTO</name> <description>A few extra python functions demonstrating the API.</description> </information> <loader type="Gnumeric_PythonLoader:python"> <attribute name="module_name" value="my-func"/> 3 </loader> <services> <service type="function_group" id="example"> 4 <category>Local Python</category> <functions> </functions> </service> </services> </plugin>
The value of "name" determines the name of your python script (file). In this case, it must be "my-func.py"
The value of "id" here determines the name of the function dictionary in your python script. In this case, it must be "example_functions" because here the value is "example".
-
Prepare to write the spells: Next we'll create a minimal python file. As noted above, we must name the file my-func.py and it must have a dictionary called example_functions. So open up my-func.py and insert the following lines.
# my-func.py # from Gnumeric import GnumericError, GnumericErrorVALUE import Gnumeric import string example_functions = { }
18.3.4.2. Writing new spells
To add new functions to Python, you now must do five things (three sir!):
Write the python function in your copy of my-func.py.
Insert the function info into the example_functions dictionary at the end of my_func.py
Insert the function name into the functions list at the end of plugin.xml.
Writing a simple script: Let's do something very simple: add two numbers together. First, edit my-func.py.
# Add two numbers together def func_add(num1, num2): return num1 + num2 # Translate the func_add python function to a gnumeric function and register it example_functions = { 'py_add': func_add }
Then let the plugin-loader(?) know about your function. Add the following line near the end of plugin.xml (between <functions> and </functions>).
<function name="py_add"/>
Now start Gnumeric and type py_add(2,3) into a cell. You should get "5". You can also use cell references. If that was in cell A1, go to cell A2 and type py_add(A1,3) and you will get "8". But your function won't show up in the GUI list yet.
Tell the GUI: To make your function show up in the GUI, you have to tell Gnumeric some things about it via a standard header, like this:
# Add two numbers together
def func_add(num1, num2):
'@FUNCTION=PY_ADD\n'\
'@SYNTAX=py_add(num1, num2)\n'\
'@DESCRIPTION=Adds two numbers together.\n'\
'Look, the description can go onto other lines.\n\n'\
'@EXAMPLES=To add two constants, just type them in: py_add(2,3)\n'\
'To add two cells, use the cell addresses: py_add(A1,A2)\n\n'\
'@SEEALSO='
return num1 + num2
The text after '@DESCRIPTION=' is the description that shows up in the function GUI. You can make it as simple or detailed as you want. I'm not sure how many other fields get used right now, as I haven't seen the EXAMPLES show up anywhere.
But this still isn't quite right. Gnumeric doesn't know how many arguments the function can handle, nor of what type. So the function GUI will prompt for the two values it knows about (as type "Any") and then keep prompting for more. But py_add cannot accept all types, nor can it handle more than two arguments, so unless you give it precisely 2 numbers, you will get an error when you click "OK".
Know your limits... We got away last time just because Gnumeric was forgiving. Now we need to say that we can accept only 2 values, of type floating-point (which will also handle ints).
Where before we had: 'py_add': func_add, we should now put: 'py_add': ('ff','num1,num2',func_add) This says that Gnumeric should expect two floating-point numbers ('ff') with names 'num1' and 'num2', and pass them to func_add.
...and surpass them Of course, there is no reason an add function shouldn't be able to handle a range. The simplest way to do that is to accept a range, and then call Gnumeric's own SUM function on it! All of Gnumeric's functions are available to you in the dictionary Gnumeric.functions, keyed by name. So here is how to write py_sum.
-
First, define func_sum (in my-func.py):
def func_sum(gRange): '@FUNCTION=PY_SUM\n'\ '@SYNTAX=PY_SUM(range)\n'\ '@DESCRIPTION=Adds a range of numbers together.'\ 'Just like built-in SUM.\n\n'\ '@EXAMPLES=To add values in A1 to A5, just type them in:\n'\ ' py_sum(a1:a5)\n'\ '@SEEALSO=' try: sum = Gnumeric.functions['sum'] val = sum(gRange) # val = reduce(lambda a,b: a+b, vals) except TypeError: raise GnumericError, GnumericErrorVALUE else: return val
-
Then insert it into your functions dictionary. That dictionary now looks like this (with 'r' denoting a range type):
example_functions = { 'py_add': ('ff','num1,num2',func_add), 'py_sum': ('r', 'values', func_sum) } -
Finally, make an entry in the XML list, so that it now looks like:
<functions> <function name="py_add"/> <function name="py_sum"/> </functions>
I told you this was the easy way to do it. Obviously it's not very useful to just duplicate Gnumeric functions. But that's as far as I've made it. From what can tell, range objects are packaged as opaque pointers of type RangeRefObject. There seems to be no way to work with them from within Python, so we must rely on the Gnumeric functions.
18.3.4.3. Do it yourself (mostly)
All is not lost, despite the opaque pointers. For in Gnumeric we can read about all the functions that have been defined. Some of those take references (including RangeRefs) and return useful information. For example, under "Lookup" we find "Column" and "Row" which return arrays of all the column (or row) indices in the range. So we can redo the sum function.
Presume we can convert our RangeRef to a start tuple and end tuple. Then we can write sum2:
def func_sum2(gRange): '@FUNCTION=PY_SUM2\n'\ '@SYNTAX=PY_SUM2(range)\n'\ '@DESCRIPTION=Adds a range of numbers together,'\ 'without calling built-in SUM.\n\n'\ '@EXAMPLES=To add values in A1 to A5, just type them in:\n'\ ' py_sum(a1:a5)\n'\ '@SEEALSO=' try: [r_begin, r_end] = range_ref_to_tuples(gRange) wb=Gnumeric.Workbooks()[0] # Careful! This is WRONG! It doesn't s=wb.sheets()[0] # use the ACTUAL workbook or sheet. val = 0 for col in range(r_begin[0], r_end[0]): for row in range(r_begin[1], r_end[1]): cell = s[col, row] val = val + cell.get_value() # Note: this doesn't skip blank cells etc. except TypeError: raise GnumericError,GnumericErrorVALUE else: return val
That's fine as far as it goes, but we need to define the helper function "range_ref_to_tuples". Although I'm rather ashamed to show this ugly literal, here's how I did it (someone suggest a better way, please!):
def range_ref_to_tuples(range_ref): '''I need a function to find the bounds of a RangeRef. This one extracts them from the Gnumeric "column" and "row" commands, and returns them as a pair of tuples. Surely there is a better way? For example, return a list of cells??''' col = Gnumeric.functions['column'] row = Gnumeric.functions['row'] # "column" and "row" take references and return an array of col or row # nums for each cell in the reference. For example, [[1, 1, 1], [2, 2, 2]] # for columns and [[2, 3, 4], [2, 3, 4]] for rows. try: columns = col(range_ref) rows = row(range_ref) begin_col = columns[0][0] - 1 begin_row = rows[0][0] - 1 end_col = columns[-1][-1] end_row = rows[-1][-1] # We subtracted 1 from the begin values because in the API, # indexing begins at 0, while "column" and "row" begin at 1. # We did NOT subtract 1 from the end values, in order to make # them suitable for Python's range(begin, end) paradigm. except TypeError: raise GnumericError,GnumericErrorVALUE except NameError: # right name? raise GnumericError,Gnumeric.GnumericErrorNAME except RefError: # right name? raise GnumericError,Gnumeric.GnumericErrorREF except NumError: # right name? raise GnumericError,Gnumeric.GnumericErrorNUM return [ (begin_col, begin_row), (end_col, end_row) ]
From there, insert the function into the dictionary, and insert its name into plugin.xml. I leave these as exercises to the reader (answers in the sample files -- no peeking!). Restart Gnumeric and you should be able to use py_sum2!
There are a couple of glitches:
- It fails the first time with "could not import gobject". Just run again, I don't know what that's about.
- It will only work for Workbook 1 and Sheet 1. JK thinks that there may be no way to get the current Workbook/Sheet in the Python API. Hrm....
- As noted, it should do some simple trapping to skip blank or text-filled cells. That can be done! I just didn't. It's late.
18.3.4.4. More help
Relative to the source tree:
- The Python interface is defined in: plugins/python-loader/py-gnumeric.c That file also has good notes at the beginning.
- There are interesting things about the way it used to be in: doc/developer/python-gnumeric.txt.
18.3.5. Upgrading
To upgrade, first choose any method from the installation section above. But note: when you upgrade your Gnumeric version, it will look for your Python scripts in the corresponding version-named subdirectories. For example, if your scripts are in "~/.gnumeric/1.1.17/plugins", but you just upgraded to 1.1.18, you may need to rename that to "~/.gnumeric/1.1.18/plugins". If you want to keep and run several versions of Gnumeric, you'll have to copy or symlink them.
If you want the Python console, you'll also have to re-enable it, following the directions above. If you had made a local copy of the old one, make sure you don't copy or link that to the new directory. It won't work.
Find the new version with gnumeric --version, making sure to invoke the proper gnumeric.
18.3.6. Fancy tricks
To be written....
- Swapping ranges (not a normal cell function, but I wrote one) that did this. But now I can rewrite it using the GUI, which will make a lot more sense.
- JK's python-only transpose function
- A Gnumeric interface to the Snob clustering algorithm. Coming soon to a spreadsheet near you!
A. Function Reference
This appendix provides a list of all the functions which are currently defined in Gnumeric.
- A.1. Bitwise Operations
- A.2. Complex
- A.3. Database
- A.4. Date/Time
- A.5. Engineering
- A.6. Erlang
- A.7. Finance
- A.8. Gnumeric
- A.9. Information
- A.10. Logic
- A.11. Lookup
- A.12. Mathematics
- A.13. Number Theory
- A.14. Random Numbers
- A.15. Statistics
- A.16. String
- A.17. Time Series Analysis
A.1. Bitwise Operations
BITAND
Synopsis
BITAND(a,b)
Arguments
a: non-negative integer
b: non-negative integer
Description
BITAND returns the bitwise and of the binary representations of its arguments.
BITLSHIFT
Synopsis
BITLSHIFT(a,n)
Arguments
a: non-negative integer
n: integer
Description
BITLSHIFT returns the binary representations of a shifted n positions to the left.
Note
If n is negative, BITLSHIFT shifts the bits to the right by ABS(n) positions.
See also
BITOR
Synopsis
BITOR(a,b)
Arguments
a: non-negative integer
b: non-negative integer
Description
BITOR returns the bitwise or of the binary representations of its arguments.
BITRSHIFT
Synopsis
BITRSHIFT(a,n)
Arguments
a: non-negative integer
n: integer
Description
BITRSHIFT returns the binary representations of a shifted n positions to the right.
Note
If n is negative, BITRSHIFT shifts the bits to the left by ABS(n) positions.
See also
A.2. Complex
- COMPLEX — a complex number of the form x + yi
- IMABS — the absolute value of the complex number z
- IMAGINARY — the imaginary part of the complex number z
- IMARCCOS — the complex arccosine of the complex number
- IMARCCOSH — the complex hyperbolic arccosine of the complex number z
- IMARCCOT — the complex arccotangent of the complex number z
- IMARCCOTH — the complex hyperbolic arccotangent of the complex number z
- IMARCCSC — the complex arccosecant of the complex number z
- IMARCCSCH — the complex hyperbolic arccosecant of the complex number z
- IMARCSEC — the complex arcsecant of the complex number z
- IMARCSECH — the complex hyperbolic arcsecant of the complex number z
- IMARCSIN — the complex arcsine of the complex number z
- IMARCSINH — the complex hyperbolic arcsine of the complex number z
- IMARCTAN — the complex arctangent of the complex number
- IMARCTANH — the complex hyperbolic arctangent of the complex number z
- IMARGUMENT — the argument theta of the complex number z
- IMCONJUGATE — the complex conjugate of the complex number z
- IMCOS — the cosine of the complex number z
- IMCOSH — the hyperbolic cosine of the complex number z
- IMCOT — the cotangent of the complex number z
- IMCOTH — the hyperbolic cotangent of the complex number z
- IMCSC — the cosecant of the complex number z
- IMCSCH — the hyperbolic cosecant of the complex number z
- IMDIV — the quotient of two complex numbers z1/z2
- IMEXP — the exponential of the complex number z
- IMFACT — the factorial of the complex number z
- IMGAMMA — the gamma function of the complex number z
- IMIGAMMA — the incomplete Gamma function
- IMINV — the reciprocal, or inverse, of the complex number z
- IMLN — the natural logarithm of the complex number z
- IMLOG10 — the base-10 logarithm of the complex number z
- IMLOG2 — the base-2 logarithm of the complex number z
- IMNEG — the negative of the complex number z
- IMPOWER — the complex number z1 raised to the z2th power
- IMPRODUCT — the product of the given complex numbers
- IMREAL — the real part of the complex number z
- IMSEC — the secant of the complex number z
- IMSECH — the hyperbolic secant of the complex number z
- IMSIN — the sine of the complex number z
- IMSINH — the hyperbolic sine of the complex number z
- IMSQRT — the square root of the complex number z
- IMSUB — the difference of two complex numbers
- IMSUM — the sum of the given complex numbers
- IMTAN — the tangent of the complex number z
- IMTANH — the hyperbolic tangent of the complex number z
COMPLEX
Synopsis
COMPLEX(x,y,i)
Arguments
x: real part
y: imaginary part
i: the suffix for the complex number, either "i" or "j"; defaults to "i"
Note
If i is neither "i" nor "j", COMPLEX returns #VALUE!
Microsoft Excel Compatibility
This function is Excel compatible.
IMABS
Synopsis
IMABS(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
IMAGINARY
Synopsis
IMAGINARY(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMARCCOS
Synopsis
IMARCCOS(z)
Arguments
z: a complex number
Description
IMARCCOS returns the complex arccosine of the complex number z. The branch cuts are on the real axis, less than -1 and greater than 1.
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCCOSH
Synopsis
IMARCCOSH(z)
Arguments
z: a complex number
Description
IMARCCOSH returns the complex hyperbolic arccosine of the complex number z. The branch cut is on the real axis, less than 1.
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCCOT
Synopsis
IMARCCOT(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCCOTH
Synopsis
IMARCCOTH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCCSC
Synopsis
IMARCCSC(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCCSCH
Synopsis
IMARCCSCH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCSEC
Synopsis
IMARCSEC(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCSECH
Synopsis
IMARCSECH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCSIN
Synopsis
IMARCSIN(z)
Arguments
z: a complex number
Description
IMARCSIN returns the complex arcsine of the complex number z. The branch cuts are on the real axis, less than -1 and greater than 1.
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCSINH
Synopsis
IMARCSINH(z)
Arguments
z: a complex number
Description
IMARCSINH returns the complex hyperbolic arcsine of the complex number z. The branch cuts are on the imaginary axis, below -i and above i.
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCTAN
Synopsis
IMARCTAN(z)
Arguments
z: a complex number
Description
IMARCTAN returns the complex arctangent of the complex number z. The branch cuts are on the imaginary axis, below -i and above i.
Note
If z is not a valid complex number, #VALUE! is returned.
IMARCTANH
Synopsis
IMARCTANH(z)
Arguments
z: a complex number
Description
IMARCTANH returns the complex hyperbolic arctangent of the complex number z. The branch cuts are on the real axis, less than -1 and greater than 1.
Note
If z is not a valid complex number, #VALUE! is returned.
IMARGUMENT
Synopsis
IMARGUMENT(z)
Arguments
z: a complex number
Description
The argument theta of a complex number is its angle in radians from the real axis.
Note
If z is not a valid complex number, #VALUE! is returned. If z is 0, 0 is returned. This is different from Excel which returns an error.
IMCONJUGATE
Synopsis
IMCONJUGATE(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
IMCOS
Synopsis
IMCOS(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
IMCOSH
Synopsis
IMCOSH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMCOT
Synopsis
IMCOT(z)
Arguments
z: a complex number
Description
IMCOT(z) = IMCOS(z)/IMSIN(z).
Note
If z is not a valid complex number, #VALUE! is returned.
IMCOTH
Synopsis
IMCOTH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMCSC
Synopsis
IMCSC(z)
Arguments
z: a complex number
Description
IMCSC(z) = 1/IMSIN(z).
Note
If z is not a valid complex number, #VALUE! is returned.
IMCSCH
Synopsis
IMCSCH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMDIV
Synopsis
IMDIV(z1,z2)
Arguments
z1: a complex number
z2: a complex number
Note
If z1 or z2 is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMEXP
Synopsis
IMEXP(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMLN.
IMFACT
Synopsis
IMFACT(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
See also
IMGAMMA
Synopsis
IMGAMMA(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
See also
IMIGAMMA
Synopsis
IMIGAMMA(a,z,lower,regularize)
Arguments
a: a complex number
z: a complex number
lower: if true (the default), the lower incomplete gamma function, otherwise the upper incomplete gamma function
regularize: if true (the default), the regularized version of the incomplete gamma function
Note
The regularized incomplete gamma function is the unregularized incomplete gamma function divided by GAMMA(a).
IMINV
Synopsis
IMINV(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMLN
Synopsis
IMLN(z)
Arguments
z: a complex number
Description
The result will have an imaginary part between -π and +π.
The natural logarithm is not uniquely defined on complex numbers. You may need to add or subtract an even multiple of π to the imaginary part.
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
IMLOG10
Synopsis
IMLOG10(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
IMLOG2
Synopsis
IMLOG2(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
IMNEG
Synopsis
IMNEG(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMPOWER
Synopsis
IMPOWER(z1,z2)
Arguments
z1: a complex number
z2: a complex number
Note
If z1 or z2 is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMPRODUCT
Synopsis
IMPRODUCT(z1,z2,…)
Arguments
z1: a complex number
z2: a complex number
Note
If any of z1, z2,... is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMREAL
Synopsis
IMREAL(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMSEC
Synopsis
IMSEC(z)
Arguments
z: a complex number
Description
IMSEC(z) = 1/IMCOS(z).
Note
If z is not a valid complex number, #VALUE! is returned.
IMSECH
Synopsis
IMSECH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMSIN
Synopsis
IMSIN(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
IMSINH
Synopsis
IMSINH(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
IMSQRT
Synopsis
IMSQRT(z)
Arguments
z: a complex number
Note
If z is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMSUB
Synopsis
IMSUB(z1,z2)
Arguments
z1: a complex number
z2: a complex number
Note
If z1 or z2 is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
IMSUM
Synopsis
IMSUM(z1,z2,…)
Arguments
z1: a complex number
z2: a complex number
Note
If any of z1, z2,... is not a valid complex number, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
A.3. Database
- DAVERAGE — average of the values in field in database belonging to records that match criteria
- DCOUNT — count of numbers in field in database belonging to records that match criteria
- DCOUNTA — count of cells with data in field in database belonging to records that match criteria
- DGET — a value from field in database belonging to records that match criteria
- DMAX — largest number in field in database belonging to a record that match criteria
- DMIN — smallest number in field in database belonging to a record that match criteria
- DPRODUCT — product of all values in field in database belonging to records that match criteria
- DSTDEV — sample standard deviation of the values in field in database belonging to records that match criteria
- DSTDEVP — standard deviation of the population of values in field in database belonging to records that match criteria
- DSUM — sum of the values in field in database belonging to records that match criteria
- DVAR — sample variance of the values in field in database belonging to records that match criteria
- DVARP — variance of the population of values in field in database belonging to records that match criteria
- GETPIVOTDATA — summary data from a pivot table
DAVERAGE
Synopsis
DAVERAGE(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DCOUNT
Synopsis
DCOUNT(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
DCOUNTA
Synopsis
DCOUNTA(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DGET
Synopsis
DGET(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
Note
If none of the records match the conditions, DGET returns #VALUE! If more than one record match the conditions, DGET returns #NUM!
See also
DMAX
Synopsis
DMAX(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DMIN.
DMIN
Synopsis
DMIN(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DPRODUCT
Synopsis
DPRODUCT(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DSUM.
DSTDEV
Synopsis
DSTDEV(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DSTDEVP
Synopsis
DSTDEVP(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DSUM
Synopsis
DSUM(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DVAR
Synopsis
DVAR(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DVARP
Synopsis
DVARP(database,field,criteria)
Arguments
database: a range in which rows of related information are records and columns of data are fields
field: a string or integer specifying which field is to be used
criteria: a range containing conditions
Description
database is a range in which rows of related information are records and columns of data are fields. The first row of a database contains labels for each column.
field is a string or integer specifying which field is to be used. If field is an integer n then the nth column will be used. If field is a string, then the column with the matching label will be used.
criteria is a range containing conditions. The first row of a criteria should contain labels. Each label specifies to which field the conditions given in that column apply. Each cell below the label specifies a condition such as ">3" or "<9". An equality condition can be given by simply specifying a value, e. g. "3" or "Jody". For a record to be considered it must satisfy all conditions in at least one of the rows of criteria.
See also
DVAR.
GETPIVOTDATA
Synopsis
GETPIVOTDATA(pivot_table,field_name)
Arguments
pivot_table: cell range containing the pivot table
field_name: name of the field for which the summary data is requested
Note
If the summary data is unavailable, GETPIVOTDATA returns #REF!
A.4. Date/Time
- ASCENSIONTHURSDAY — Ascension Thursday in the Gregorian calendar according to the Roman rite of the Christian Church
- ASHWEDNESDAY — Ash Wednesday in the Gregorian calendar according to the Roman rite of the Christian Church
- DATE — create a date serial value
- DATE2HDATE — Hebrew date
- DATE2HDATE_HEB — Hebrew date in Hebrew
- DATE2JULIAN — Julian day number for given Gregorian date
- DATE2UNIX — the Unix timestamp corresponding to a date d
- DATEDIF — difference between dates
- DATEVALUE — the date part of a date and time serial value
- DAY — the day-of-month part of a date serial value
- DAYS — difference between dates in days
- DAYS360 — days between dates
- EASTERSUNDAY — Easter Sunday in the Gregorian calendar according to the Roman rite of the Christian Church
- EDATE — adjust a date by a number of months
- EOMONTH — end of month
- GOODFRIDAY — Good Friday in the Gregorian calendar according to the Roman rite of the Christian Church
- HDATE — Hebrew date
- HDATE_DAY — Hebrew day of Gregorian date
- HDATE_HEB — Hebrew date in Hebrew
- HDATE_JULIAN — Julian day number for given Gregorian date
- HDATE_MONTH — Hebrew month of Gregorian date
- HDATE_YEAR — Hebrew year of Gregorian date
- HOUR — compute hour part of fractional day
- ISOWEEKNUM — ISO week number
- ISOYEAR — year corresponding to the ISO week number
- MINUTE — compute minute part of fractional day
- MONTH — the month part of a date serial value
- NETWORKDAYS — number of workdays in range
- NOW — the date and time serial value of the current time
- ODF.TIME — create a time serial value
- PENTECOSTSUNDAY — Pentecost Sunday in the Gregorian calendar according to the Roman rite of the Christian Church
- SECOND — compute seconds part of fractional day
- TIME — create a time serial value
- TIMEVALUE — the time part of a date and time serial value
- TODAY — the date serial value of today
- UNIX2DATE — date value corresponding to the Unix timestamp t
- WEEKDAY — day-of-week
- WEEKNUM — week number
- WORKDAY — add working days
- YEAR — the year part of a date serial value
- YEARFRAC — fractional number of years between dates
ASCENSIONTHURSDAY
Synopsis
ASCENSIONTHURSDAY(year)
Arguments
year: year between 1582 and 9956, defaults to the year of the next Ascension Thursday
Note
Two digit years are adjusted as elsewhere in Gnumeric. Dates before 1904 may also be prohibited.
See also
ASHWEDNESDAY
Synopsis
ASHWEDNESDAY(year)
Arguments
year: year between 1582 and 9956, defaults to the year of the next Ash Wednesday
Note
Two digit years are adjusted as elsewhere in Gnumeric. Dates before 1904 may also be prohibited.
See also
DATE
Synopsis
DATE(year,month,day)
Arguments
year: year of date
month: month of year
day: day of month
Description
The DATE function creates date serial values. 1-Jan-1900 is serial value 1, 2-Jan-1900 is serial value 2, and so on. For compatibility reasons, a serial value is reserved for the non-existing date 29-Feb-1900.
Note
If month or day is less than 1 or too big, then the year and/or month will be adjusted. For spreadsheets created with the Mac version of Excel, serial 1 is 1-Jan-1904.
Microsoft Excel Compatibility
This function is Excel compatible.
DATE2HDATE
Synopsis
DATE2HDATE(date)
Arguments
date: Gregorian date, defaults to today
See also
DATE2HDATE_HEB
Synopsis
DATE2HDATE_HEB(date)
Arguments
date: Gregorian date, defaults to today
See also
DATE2JULIAN
Synopsis
DATE2JULIAN(date)
Arguments
date: Gregorian date, defaults to today
See also
DATE2UNIX
Synopsis
DATE2UNIX(d)
Arguments
d: date
Description
The DATE2UNIX function translates a date into a Unix timestamp. A Unix timestamp is the number of seconds since midnight (0:00) of January 1st, 1970 GMT.
DATEDIF
Synopsis
DATEDIF(start_date,end_date,interval)
Arguments
start_date: starting date serial value
end_date: ending date serial value
interval: counting unit
Description
DATEDIF returns the distance from start_date to end_date according to the unit specified by interval.
Note
If interval is "y", "m", or "d" then the distance is measured in complete years, months, or days respectively. If interval is "ym" or "yd" then the distance is measured in complete months or days, respectively, but excluding any difference in years. If interval is "md" then the distance is measured in complete days but excluding any difference in months.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
DATEVALUE
Synopsis
DATEVALUE(serial)
Arguments
serial: date and time serial value
Description
DATEVALUE returns the date serial value part of a date and time serial value.
Microsoft Excel Compatibility
This function is Excel compatible.
DAY
Synopsis
DAY(date)
Arguments
date: date serial value
Description
The DAY function returns the day-of-month part of date.
Microsoft Excel Compatibility
This function is Excel compatible.
DAYS
Synopsis
DAYS(end_date,start_date)
Arguments
end_date: ending date serial value
start_date: starting date serial value
Description
DAYS returns the positive or negative number of days from start_date to end_date.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
DAYS360
Synopsis
DAYS360(start_date,end_date,method)
Arguments
start_date: starting date serial value
end_date: ending date serial value
method: counting method
Description
DAYS360 returns the number of days from start_date to end_date.
Note
If method is 0, the default, the MS Excel (tm) US method will be used. This is a somewhat complicated industry standard method where the last day of February is considered to be the 30th day of the month, but only for start_date. If method is 1, the European method will be used. In this case, if the day of the month is 31 it will be considered as 30 If method is 2, a saner version of the US method is used in which both dates get the same February treatment.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
EASTERSUNDAY
Synopsis
EASTERSUNDAY(year)
Arguments
year: year between 1582 and 9956, defaults to the year of the next Easter Sunday
Note
Two digit years are adjusted as elsewhere in Gnumeric. Dates before 1904 may also be prohibited.
OpenDocument Format (ODF) Compatibility
The 1-argument version of EASTERSUNDAY is compatible with OpenOffice for years after 1904. This function is not specified in ODF/OpenFormula.
See also
EDATE
Synopsis
EDATE(date,months)
Arguments
date: date serial value
months: signed number of months
Description
EDATE returns date moved forward or backward the number of months specified by months.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
DATE.
EOMONTH
Synopsis
EOMONTH(date,months)
Arguments
date: date serial value
months: signed number of months
Description
EOMONTH returns the date serial value of the end of the month specified by date adjusted forward or backward the number of months specified by months.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
GOODFRIDAY
Synopsis
GOODFRIDAY(year)
Arguments
year: year between 1582 and 9956, defaults to the year of the next Good Friday
Note
Two digit years are adjusted as elsewhere in Gnumeric. Dates before 1904 may also be prohibited.
See also
HDATE
Synopsis
HDATE(year,month,day)
Arguments
year: Gregorian year of date, defaults to the current year
month: Gregorian month of year, defaults to the current month
day: Gregorian day of month, defaults to the current day
HDATE_DAY
Synopsis
HDATE_DAY(year,month,day)
Arguments
year: Gregorian year of date, defaults to the current year
month: Gregorian month of year, defaults to the current month
day: Gregorian day of month, defaults to the current day
See also
HDATE_HEB
Synopsis
HDATE_HEB(year,month,day)
Arguments
year: Gregorian year of date, defaults to the current year
month: Gregorian month of year, defaults to the current month
day: Gregorian day of month, defaults to the current day
HDATE_JULIAN
Synopsis
HDATE_JULIAN(year,month,day)
Arguments
year: Gregorian year of date, defaults to the current year
month: Gregorian month of year, defaults to the current month
day: Gregorian day of month, defaults to the current day
See also
HDATE_MONTH
Synopsis
HDATE_MONTH(year,month,day)
Arguments
year: Gregorian year of date, defaults to the current year
month: Gregorian month of year, defaults to the current month
day: Gregorian day of month, defaults to the current day
See also
HDATE_YEAR
Synopsis
HDATE_YEAR(year,month,day)
Arguments
year: Gregorian year of date, defaults to the current year
month: Gregorian month of year, defaults to the current month
day: Gregorian day of month, defaults to the current day
See also
HOUR
Synopsis
HOUR(time)
Arguments
time: time of day as fractional day
Description
The HOUR function computes the hour part of the fractional day given by time.
Microsoft Excel Compatibility
This function is Excel compatible.
ISOWEEKNUM
Synopsis
ISOWEEKNUM(date)
Arguments
date: date serial value
Description
ISOWEEKNUM calculates the week number according to the ISO 8601 standard. Weeks start on Mondays and week 1 contains the first Thursday of the year.
Note
January 1 of a year is sometimes in week 52 or 53 of the previous year. Similarly, December 31 is sometimes in week 1 of the following year.
ISOYEAR
Synopsis
ISOYEAR(date)
Arguments
date: date serial value
Description
ISOYEAR calculates the year to go with week number according to the ISO 8601 standard.
Note
January 1 of a year is sometimes in week 52 or 53 of the previous year. Similarly, December 31 is sometimes in week 1 of the following year.
See also
MINUTE
Synopsis
MINUTE(time)
Arguments
time: time of day as fractional day
Description
The MINUTE function computes the minute part of the fractional day given by time.
Microsoft Excel Compatibility
This function is Excel compatible.
MONTH
Synopsis
MONTH(date)
Arguments
date: date serial value
Description
The MONTH function returns the month part of date.
Microsoft Excel Compatibility
This function is Excel compatible.
NETWORKDAYS
Synopsis
NETWORKDAYS(start_date,end_date,holidays,weekend)
Arguments
start_date: starting date serial value
end_date: ending date serial value
holidays: array of holidays
weekend: array of 0s and 1s, indicating whether a weekday (S, M, T, W, T, F, S) is on the weekend, defaults to {1,0,0,0,0,0,1}
Description
NETWORKDAYS calculates the number of days from start_date to end_date skipping weekends and holidays in the process.
Note
If an entry of weekend is non-zero, the corresponding weekday is not a work day.
Microsoft Excel Compatibility
This function is Excel compatible if the last argument is omitted.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
NOW
Synopsis
NOW()Description
The NOW function returns the date and time serial value of the moment it is computed. Recomputing later will produce a different value.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
DATE.
ODF.TIME
Synopsis
ODF.TIME(hour,minute,second)
Arguments
hour: hour
minute: minute
second: second
Description
The ODF.TIME function computes the time given by hour, minute, and second as a fraction of a day.
Note
While the return value is automatically formatted to look like a time between 0:00 and 24:00, the underlying serial time value can be any number.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
PENTECOSTSUNDAY
Synopsis
PENTECOSTSUNDAY(year)
Arguments
year: year between 1582 and 9956, defaults to the year of the next Pentecost Sunday
Note
Two digit years are adjusted as elsewhere in Gnumeric. Dates before 1904 may also be prohibited.
See also
SECOND
Synopsis
SECOND(time)
Arguments
time: time of day as fractional day
Description
The SECOND function computes the seconds part of the fractional day given by time.
Microsoft Excel Compatibility
This function is Excel compatible.
TIME
Synopsis
TIME(hour,minute,second)
Arguments
hour: hour of the day
minute: minute within the hour
second: second within the minute
Description
The TIME function computes the fractional day after midnight at the time given by hour, minute, and second.
Note
While the return value is automatically formatted to look like a time between 0:00 and 24:00, the underlying serial time value is a number between 0 and 1. If any of hour, minute, and second is negative, #NUM! is returned
Microsoft Excel Compatibility
This function is Excel compatible.
TIMEVALUE
Synopsis
TIMEVALUE(serial)
Arguments
serial: date and time serial value
Description
TIMEVALUE returns the time-of-day part of a date and time serial value.
Microsoft Excel Compatibility
This function is Excel compatible.
TODAY
Synopsis
TODAY()Description
The TODAY function returns the date serial value of the day it is computed. Recomputing on a later date will produce a different value.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
DATE.
UNIX2DATE
Synopsis
UNIX2DATE(t)
Arguments
t: Unix time stamp
Description
The UNIX2DATE function translates Unix timestamps into the corresponding date. A Unix timestamp is the number of seconds since midnight (0:00) of January 1st, 1970 GMT.
WEEKDAY
Synopsis
WEEKDAY(date,method)
Arguments
date: date serial value
method: numbering system, defaults to 1
Description
The WEEKDAY function returns the day-of-week of date. The value of method determines how days are numbered; it defaults to 1.
Note
If method is 1, then Sunday is 1, Monday is 2, etc. If method is 2, then Monday is 1, Tuesday is 2, etc. If method is 3, then Monday is 0, Tuesday is 1, etc. If method is 11, then Monday is 1, Tuesday is 2, etc. If method is 12, then Tuesday is 1, Wednesday is 2, etc. If method is 13, then Wednesday is 1, Thursday is 2, etc. If method is 14, then Thursday is 1, Friday is 2, etc. If method is 15, then Friday is 1, Saturday is 2, etc. If method is 16, then Saturday is 1, Sunday is 2, etc. If method is 17, then Sunday is 1, Monday is 2, etc.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
WEEKNUM
Synopsis
WEEKNUM(date,method)
Arguments
date: date serial value
method: numbering system, defaults to 1
Description
WEEKNUM calculates the week number according to method which defaults to 1.
Note
If method is 1, then weeks start on Sundays and January 1 is in week 1. If method is 2, then weeks start on Mondays and January 1 is in week 1. If method is 150, then the ISO 8601 numbering is used.
See also
WORKDAY
Synopsis
WORKDAY(date,days,holidays,weekend)
Arguments
date: date serial value
days: number of days to add
holidays: array of holidays
weekend: array of 0s and 1s, indicating whether a weekday (S, M, T, W, T, F, S) is on the weekend, defaults to {1,0,0,0,0,0,1}
Description
WORKDAY adjusts date by days skipping over weekends and holidays in the process.
Note
days may be negative. If an entry of weekend is non-zero, the corresponding weekday is not a work day.
Microsoft Excel Compatibility
This function is Excel compatible if the last argument is omitted.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
YEAR
Synopsis
YEAR(date)
Arguments
date: date serial value
Description
The YEAR function returns the year part of date.
Microsoft Excel Compatibility
This function is Excel compatible.
YEARFRAC
Synopsis
YEARFRAC(start_date,end_date,basis)
Arguments
start_date: starting date serial value
end_date: ending date serial value
basis: calendar basis
Description
YEARFRAC calculates the number of days from start_date to end_date according to the calendar specified by basis, which defaults to 0, and expresses the result as a fractional number of years.
Note
If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
DATE.
A.5. Engineering
- BASE — string of digits representing the number n in base b
- BESSELI — Modified Bessel function of the first kind of order α at x
- BESSELJ — Bessel function of the first kind of order α at x
- BESSELK — Modified Bessel function of the second kind of order α at x
- BESSELY — Bessel function of the second kind of order α at x
- BIN2DEC — decimal representation of the binary number x
- BIN2HEX — hexadecimal representation of the binary number x
- BIN2OCT — octal representation of the binary number x
- CONVERT — a converted measurement
- DEC2BIN — binary representation of the decimal number x
- DEC2HEX — hexadecimal representation of the decimal number x
- DEC2OCT — octal representation of the decimal number x
- DECIMAL — decimal representation of x
- DELTA — Kronecker delta function
- ERF — Gauss error function
- ERFC — Complementary Gauss error function
- GESTEP — step function with step at x1 evaluated at x0
- HEX2BIN — binary representation of the hexadecimal number x
- HEX2DEC — decimal representation of the hexadecimal number x
- HEX2OCT — octal representation of the hexadecimal number x
- HEXREP — hexadecimal representation of numeric value
- INVSUMINV — the reciprocal of the sum of reciprocals of the arguments
- OCT2BIN — binary representation of the octal number x
- OCT2DEC — decimal representation of the octal number x
- OCT2HEX — hexadecimal representation of the octal number x
BASE
Synopsis
BASE(n,b,length)
Arguments
n: integer
b: base (2 ≤ b ≤ 36)
length: minimum length of the resulting string
Description
BASE converts n to its string representation in base b. Leading zeroes will be added to reach the minimum length given by length.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
BESSELI
Synopsis
BESSELI(X,α)
Arguments
X: number
α: order (any non-negative number)
Note
If x or α are not numeric, #VALUE! is returned. If α < 0, #NUM! is returned.
Microsoft Excel Compatibility
This function is Excel compatible if only integer orders α are used.
BESSELJ
Synopsis
BESSELJ(X,α)
Arguments
X: number
α: order (any non-negative integer)
Note
If x or α are not numeric, #VALUE! is returned. If α < 0, #NUM! is returned.
Microsoft Excel Compatibility
This function is Excel compatible if only integer orders α are used.
BESSELK
Synopsis
BESSELK(X,α)
Arguments
X: number
α: order (any non-negative number)
Note
If x or α are not numeric, #VALUE! is returned. If α < 0, #NUM! is returned.
Microsoft Excel Compatibility
This function is Excel compatible if only integer orders α are used.
BESSELY
Synopsis
BESSELY(X,α)
Arguments
X: number
α: order (any non-negative integer)
Note
If x or α are not numeric, #VALUE! is returned. If α < 0, #NUM! is returned.
Microsoft Excel Compatibility
This function is Excel compatible if only integer orders α are used.
BIN2DEC
Synopsis
BIN2DEC(x)
Arguments
x: a binary number, either as a string or as a number involving only the digits 0 and 1
Microsoft Excel Compatibility
This function is Excel compatible.
BIN2HEX
Synopsis
BIN2HEX(x,places)
Arguments
x: a binary number, either as a string or as a number involving only the digits 0 and 1
places: number of digits
Description
If places is given, BIN2HEX pads the result with zeros to achieve exactly places digits. If this is not possible, BIN2HEX returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
BIN2OCT
Synopsis
BIN2OCT(x,places)
Arguments
x: a binary number, either as a string or as a number involving only the digits 0 and 1
places: number of digits
Description
If places is given, BIN2OCT pads the result with zeros to achieve exactly places digits. If this is not possible, BIN2OCT returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
CONVERT
Synopsis
CONVERT(x,from,to)
Arguments
x: number
from: unit (string)
to: unit (string)
Description
CONVERT returns a conversion from one measurement system to another. x is a value in from units that is to be converted into to units.
from and to can be any of the following:
Weight and mass:
'brton' Imperial ton
'cwt' U.S. (short) hundredweight
'g' Gram
'grain' Grain
'hweight' Imperial (long) hundredweight
'LTON' Imperial ton
'sg' Slug
'shweight' U.S. (short) hundredweight
'lbm' Pound
'lcwt' Imperial (long) hundredweight
'u' U (atomic mass)
'uk_cwt' Imperial (long) hundredweight
'uk_ton' Imperial ton
'ozm' Ounce
'stone' Stone
'ton' Ton
Distance:
'm' Meter
'mi' Statute mile
'survey_mi' U.S. survey mile
'Nmi' Nautical mile
'in' Inch
'ft' Foot
'yd' Yard
'ell' English Ell
'ang' Angstrom
'ly' Light-Year
'pc' Parsec
'parsec' Parsec
'Pica' Pica Points
'Picapt' Pica Points
'picapt' Pica Points
'pica' Pica
Time:
'yr' Year
'day' Day
'hr' Hour
'mn' Minute
'sec' Second
Pressure:
'Pa' Pascal
'psi' PSI
'atm' Atmosphere
'Pa' Pascal
'mmHg' mm of Mercury
'Torr' Torr
Force:
'N' Newton
'dyn' Dyne
'pond' Pond
'lbf' Pound force
Energy:
'J' Joule
'e' Erg
'c' Thermodynamic calorie
'cal' IT calorie
'eV' Electron volt
'HPh' Horsepower-hour
'Wh' Watt-hour
'flb' Foot-pound
'BTU' BTU
Power:
'HP' Horsepower
'PS' Pferdestärke
'W' Watt
Magnetism:
'T' Tesla
'ga' Gauss
Temperature:
'C' Degree Celsius
'F' Degree Fahrenheit
'K' Kelvin
'Rank' Degree Rankine
'Reau' Degree Réaumur
Volume (liquid measure):
'tsp' Teaspoon
'tspm' Teaspoon (modern, metric)
'tbs' Tablespoon
'oz' Fluid ounce
'cup' Cup
'pt' Pint
'us_pt' U.S. pint
'uk_pt' Imperial pint (U.K.)
'qt' Quart
'uk_qt' Imperial quart
'gal' Gallon
'uk_gal' Imperial gallon
'GRT' Registered ton
'regton' Registered ton
'MTON' Measurement ton (freight ton)
'l' Liter
'L' Liter
'lt' Liter
'ang3' Cubic Angstrom
'ang^3' Cubic Angstrom
'barrel' U.S. oil barrel (bbl)
'bushel' U.S. bushel
'ft3' Cubic feet
'ft^3' Cubic feet
'in3' Cubic inch
'in^3' Cubic inch
'ly3' Cubic light-year
'ly^3' Cubic light-year
'm3' Cubic meter
'm^3' Cubic meter
'mi3' Cubic mile
'mi^3' Cubic mile
'yd3' Cubic yard
'yd^3' Cubic yard
'Nmi3' Cubic nautical mile
'Nmi^3' Cubic nautical mile
'Picapt3' Cubic Pica
'Picapt^3' Cubic Pica
'Pica3' Cubic Pica
'Pica^3' Cubic Pica
Area:
'uk_acre' International acre
'us_acre' U.S. survey/statute acre
'ang2' Square angstrom
'ang^2' Square angstrom
'ar' Are
'ha' Hectare
'in2' Square inches
'in^2' Square inches
'ly2' Square light-year
'ly^2' Square light-year
'm2' Square meter
'm^2' Square meter
'Morgen' Morgen (North German Confederation)
'mi2' Square miles
'mi^2' Square miles
'Nmi2' Square nautical miles
'Nmi^2' Square nautical miles
'Picapt2' Square Pica
'Picapt^2' Square Pica
'Pica2' Square Pica
'Pica^2' Square Pica
'yd2' Square yards
'yd^2' Square yards
Bits and Bytes:
'bit' Bit
'byte' Byte
Speed:
'admkn' Admiralty knot
'kn' knot
'm/h' Meters per hour
'm/hr' Meters per hour
'm/s' Meters per second
'm/sec' Meters per second
'mph' Miles per hour
For metric units any of the following prefixes can be used:
'Y' yotta 1E+24
'Z' zetta 1E+21
'E' exa 1E+18
'P' peta 1E+15
'T' tera 1E+12
'G' giga 1E+09
'M' mega 1E+06
'k' kilo 1E+03
'h' hecto 1E+02
'e' deca (deka) 1E+01
'd' deci 1E-01
'c' centi 1E-02
'm' milli 1E-03
'u' micro 1E-06
'n' nano 1E-09
'p' pico 1E-12
'f' femto 1E-15
'a' atto 1E-18
'z' zepto 1E-21
'y' yocto 1E-24
For bits and bytes any of the following prefixes can be also be used:
'Yi' yobi 2^80
'Zi' zebi 2^70
'Ei' exbi 2^60
'Pi' pebi 2^50
'Ti' tebi 2^40
'Gi' gibi 2^30
'Mi' mebi 2^20
'ki' kibi 2^10
Note
If from and to are different types, CONVERT returns #N/A!
Microsoft Excel Compatibility
This function is Excel compatible (except "picapt").
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
DEC2BIN
Synopsis
DEC2BIN(x,places)
Arguments
x: integer (− 513 < x < 512)
places: number of digits
Description
If places is given and x is non-negative, DEC2BIN pads the result with zeros to achieve exactly places digits. If this is not possible, DEC2BIN returns #NUM!
If places is given and x is negative, places is ignored.
Note
If x < − 512 or x > 511, DEC2BIN returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
DEC2HEX
Synopsis
DEC2HEX(x,places)
Arguments
x: integer
places: number of digits
Description
If places is given, DEC2HEX pads the result with zeros to achieve exactly places digits. If this is not possible, DEC2HEX returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
DEC2OCT
Synopsis
DEC2OCT(x,places)
Arguments
x: integer
places: number of digits
Description
If places is given, DEC2OCT pads the result with zeros to achieve exactly places digits. If this is not possible, DEC2OCT returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
DECIMAL
Synopsis
DECIMAL(x,base)
Arguments
x: number in base base
base: base of x, (2 ≤ base ≤ 36)
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
BASE.
DELTA
Synopsis
DELTA(x0,x1)
Arguments
x0: number
x1: number, defaults to 0
Description
DELTA returns 1 if x1 = x0 and 0 otherwise.
Note
If either argument is non-numeric, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
ERF
Synopsis
ERF(lower,upper)
Arguments
lower: lower limit of the integral, defaults to 0
upper: upper limit of the integral
Description
ERF returns 2/sqrt(π)* integral from lower to upper of exp(-t*t) dt
Microsoft Excel Compatibility
This function is Excel compatible if two arguments are supplied and neither is negative.
See also
ERFC.
ERFC
Synopsis
ERFC(x)
Arguments
x: number
Description
ERFC returns 2/sqrt(π)* integral from x to ∞ of exp(-t*t) dt
See also
ERF.
GESTEP
Synopsis
GESTEP(x0,x1)
Arguments
x0: number
x1: number, defaults to 0
Description
GESTEP returns 1 if x1 ≤ x0 and 0 otherwise.
Note
If either argument is non-numeric, #VALUE! is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
HEX2BIN
Synopsis
HEX2BIN(x,places)
Arguments
x: a hexadecimal number, either as a string or as a number if no A to F are needed
places: number of digits
Description
If places is given, HEX2BIN pads the result with zeros to achieve exactly places digits. If this is not possible, HEX2BIN returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
HEX2DEC
Synopsis
HEX2DEC(x)
Arguments
x: a hexadecimal number, either as a string or as a number if no A to F are needed
Microsoft Excel Compatibility
This function is Excel compatible.
HEX2OCT
Synopsis
HEX2OCT(x,places)
Arguments
x: a hexadecimal number, either as a string or as a number if no A to F are needed
places: number of digits
Description
If places is given, HEX2OCT pads the result with zeros to achieve exactly places digits. If this is not possible, HEX2OCT returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
HEXREP
Synopsis
HEXREP(x)
Arguments
x: number
Description
HEXREP returns a hexadecimal string representation of x.
Note
This is a function meant for debugging. The layout of the result may change and even depend on how Gnumeric was compiled.
INVSUMINV
Synopsis
INVSUMINV(x0,x1,…)
Arguments
x0: non-negative number
x1: non-negative number
Description
INVSUMINV sum calculates the reciprocal (the inverse) of the sum of reciprocals (inverses) of all its arguments.
Note
If any of the arguments is negative, #VALUE! is returned.
If any argument is zero, the result is zero.
See also
OCT2BIN
Synopsis
OCT2BIN(x,places)
Arguments
x: a octal number, either as a string or as a number
places: number of digits
Description
If places is given, OCT2BIN pads the result with zeros to achieve exactly places digits. If this is not possible, OCT2BIN returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
OCT2DEC
Synopsis
OCT2DEC(x)
Arguments
x: a octal number, either as a string or as a number
Microsoft Excel Compatibility
This function is Excel compatible.
OCT2HEX
Synopsis
OCT2HEX(x,places)
Arguments
x: a octal number, either as a string or as a number
places: number of digits
Description
If places is given, OCT2HEX pads the result with zeros to achieve exactly places digits. If this is not possible, OCT2HEX returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
A.6. Erlang
DIMCIRC
Synopsis
DIMCIRC(traffic,gos)
Arguments
traffic: number of calls
gos: grade of service
Description
DIMCIRC returns the number of circuits required given traffic calls with grade of service gos.
OFFCAP
Synopsis
OFFCAP(circuits,gos)
Arguments
circuits: number of circuits
gos: grade of service
Description
OFFCAP returns the traffic capacity given circuits circuits with grade of service gos.
OFFTRAF
Synopsis
OFFTRAF(traffic,circuits)
Arguments
traffic: number of carried calls
circuits: number of circuits
Description
OFFTRAF returns the predicted number of offered calls given traffic carried calls (taken from measurements) on circuits circuits.
Note
traffic cannot exceed circuits.
A.7. Finance
- ACCRINT — accrued interest
- ACCRINTM — accrued interest
- AMORDEGRC — depreciation of an asset using French accounting conventions
- AMORLINC — depreciation of an asset using French accounting conventions
- COUPDAYBS — number of days from coupon period to settlement
- COUPDAYS — number of days in the coupon period of the settlement date
- COUPDAYSNC — number of days from the settlement date to the next coupon period
- COUPNCD — the next coupon date after settlement
- COUPNUM — number of coupons
- COUPPCD — the last coupon date before settlement
- CUM_BIV_NORM_DIST — cumulative bivariate normal distribution
- CUMIPMT — cumulative interest payment
- CUMPRINC — cumulative principal
- DB — depreciation of an asset
- DDB — depreciation of an asset
- DISC — discount rate
- DOLLARDE — convert to decimal dollar amount
- DOLLARFR — convert to dollar fraction
- DURATION — the (Macaulay) duration of a security
- EFFECT — effective interest rate
- EURO — equivalent of 1 EUR
- EUROCONVERT — pre-Euro amount from one currency to another
- FV — future value
- FVSCHEDULE — future value
- G_DURATION — the duration of a investment
- INTRATE — interest rate
- IPMT — interest payment for period
- IRR — internal rate of return
- ISPMT — interest payment for period
- MDURATION — the modified (Macaulay) duration of a security
- MIRR — modified internal rate of return
- NOMINAL — nominal interest rate
- NPER — number of periods
- NPV — net present value
- ODDFPRICE — price of a security that has an odd first period
- ODDFYIELD — yield of a security that has an odd first period
- ODDLPRICE — price of a security that has an odd last period
- ODDLYIELD — yield of a security that has an odd last period
- OPT_2_ASSET_CORRELATION — theoretical price of options on 2 assets with correlation rho
- OPT_AMER_EXCHANGE — theoretical price of an American option to exchange assets
- OPT_BAW_AMER — theoretical price of an option according to the Barone Adesie & Whaley approximation
- OPT_BINOMIAL — theoretical price of either an American or European style option using a binomial tree
- OPT_BJER_STENS — theoretical price of American options according to the Bjerksund & Stensland approximation technique
- OPT_BS — price of a European option
- OPT_BS_CARRYCOST — elasticity of a European option
- OPT_BS_DELTA — delta of a European option
- OPT_BS_GAMMA — gamma of a European option
- OPT_BS_RHO — rho of a European option
- OPT_BS_THETA — theta of a European option
- OPT_BS_VEGA — vega of a European option
- OPT_COMPLEX_CHOOSER — theoretical price of a complex chooser option
- OPT_EURO_EXCHANGE — theoretical price of a European option to exchange assets
- OPT_EXEC — theoretical price of executive stock options
- OPT_EXTENDIBLE_WRITER — theoretical price of extendible writer options
- OPT_FIXED_STRK_LKBK — theoretical price of a fixed-strike lookback option
- OPT_FLOAT_STRK_LKBK — theoretical price of floating-strike lookback option
- OPT_FORWARD_START — theoretical price of forward start options
- OPT_FRENCH — theoretical price of a European option adjusted for trading day volatility
- OPT_GARMAN_KOHLHAGEN — theoretical price of a European currency option
- OPT_JUMP_DIFF — theoretical price of an option according to the Jump Diffusion process
- OPT_MILTERSEN_SCHWARTZ — theoretical price of options on commodities futures according to Miltersen & Schwartz
- OPT_ON_OPTIONS — theoretical price of options on options
- OPT_RGW — theoretical price of an American option according to the Roll-Geske-Whaley approximation
- OPT_SIMPLE_CHOOSER — theoretical price of a simple chooser option
- OPT_SPREAD_APPROX — theoretical price of a European option on the spread between two futures contracts
- OPT_TIME_SWITCH — theoretical price of time switch options
- PMT — payment for annuity
- PPMT — interest payment for period
- PRICE — price of a security
- PRICEDISC — discounted price
- PRICEMAT — price at maturity
- PV — present value
- RATE — rate of investment
- RECEIVED — amount to be received at maturity
- RRI — equivalent interest rate for an investment increasing in value
- SLN — depreciation of an asset
- SYD — sum-of-years depreciation
- TBILLEQ — bond-equivalent yield for a treasury bill
- TBILLPRICE — price of a treasury bill
- TBILLYIELD — yield of a treasury bill
- VDB — depreciation of an asset
- XIRR — internal rate of return
- XNPV — net present value
- YIELD — yield of a security
- YIELDDISC — yield of a discounted security
- YIELDMAT — yield of a security
ACCRINT
Synopsis
ACCRINT(issue,first_interest,settlement,rate,par,frequency,basis,calc_method)
Arguments
issue: date of issue
first_interest: date of first interest payment
settlement: settlement date
rate: nominal annual interest rate
par: par value, defaults to $1000
frequency: number of interest payments per year
basis: calendar basis, defaults to 0
calc_method: calculation method, defaults to TRUE
Description
If first_interest < settlement and calc_method is TRUE, then ACCRINT returns the sum of the interest accrued in all coupon periods from issue date until settlement date.
If first_interest < settlement and calc_method is FALSE, then ACCRINT returns the sum of the interest accrued in all coupon periods from first_interest date until settlement date.
Otherwise ACCRINT returns the sum of the interest accrued in all coupon periods from issue date until settlement date.
Note
frequency must be one of 1, 2 or 4, but the exact value does not affect the result. issue must precede both first_interest and settlement. frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
ACCRINTM
Synopsis
ACCRINTM(issue,maturity,rate,par,basis)
Arguments
issue: date of issue
maturity: maturity date
rate: nominal annual interest rate
par: par value
basis: calendar basis
Description
ACCRINTM calculates the accrued interest from issue to maturity.
Note
par defaults to $1000. If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
AMORDEGRC
Synopsis
AMORDEGRC(cost,purchase_date,first_period,salvage,period,rate,basis)
Arguments
cost: initial cost of asset
purchase_date: date of purchase
first_period: end of first period
salvage: value after depreciation
period: subject period
rate: depreciation rate
basis: calendar basis
Description
AMORDEGRC calculates the depreciation of an asset using French accounting conventions. Assets purchased in the middle of a period take prorated depreciation into account. This is similar to AMORLINC, except that a depreciation coefficient is applied in the calculation depending on the life of the assets.
The depreciation coefficient used is:
1.0 for an expected lifetime less than 3 years,
1.5 for an expected lifetime of at least 3 years but less than 5 years,
2.0 for an expected lifetime of at least 5 years but at most 6 years,
2.5 for an expected lifetime of more than 6 years.
Note
Special depreciation rules are applied for the last two periods resulting in a possible total depreciation exceeding the difference of cost - salvage. Named for AMORtissement DEGRessif Comptabilite. If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
AMORLINC
Synopsis
AMORLINC(cost,purchase_date,first_period,salvage,period,rate,basis)
Arguments
cost: initial cost of asset
purchase_date: date of purchase
first_period: end of first period
salvage: value after depreciation
period: subject period
rate: depreciation rate
basis: calendar basis
Description
AMORLINC calculates the depreciation of an asset using French accounting conventions. Assets purchased in the middle of a period take prorated depreciation into account.
Note
Named for AMORtissement LINeaire Comptabilite. If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
COUPDAYBS
Synopsis
COUPDAYBS(settlement,maturity,frequency,basis,eom)
Arguments
settlement: settlement date
maturity: maturity date
frequency: number of interest payments per year
basis: calendar basis
eom: end-of-month flag
Description
COUPDAYBS calculates the number of days from the beginning of the coupon period to the settlement date.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
COUPDAYS
Synopsis
COUPDAYS(settlement,maturity,frequency,basis,eom)
Arguments
settlement: settlement date
maturity: maturity date
frequency: number of interest payments per year
basis: calendar basis
eom: end-of-month flag
Description
COUPDAYS calculates the number of days in the coupon period of the settlement date.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
COUPDAYSNC
Synopsis
COUPDAYSNC(settlement,maturity,frequency,basis,eom)
Arguments
settlement: settlement date
maturity: maturity date
frequency: number of interest payments per year
basis: calendar basis
eom: end-of-month flag
Description
COUPDAYSNC calculates number of days from the settlement date to the next coupon period.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
COUPNCD
Synopsis
COUPNCD(settlement,maturity,frequency,basis,eom)
Arguments
settlement: settlement date
maturity: maturity date
frequency: number of interest payments per year
basis: calendar basis
eom: end-of-month flag
Description
COUPNCD calculates the coupon date following settlement.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
COUPNUM
Synopsis
COUPNUM(settlement,maturity,frequency,basis,eom)
Arguments
settlement: settlement date
maturity: maturity date
frequency: number of interest payments per year
basis: calendar basis
eom: end-of-month flag
Description
COUPNUM calculates the number of coupons to be paid between the settlement and maturity dates, rounded up.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
COUPPCD
Synopsis
COUPPCD(settlement,maturity,frequency,basis,eom)
Arguments
settlement: settlement date
maturity: maturity date
frequency: number of interest payments per year
basis: calendar basis
eom: end-of-month flag
Description
COUPPCD calculates the coupon date preceding settlement.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
CUM_BIV_NORM_DIST
Synopsis
CUM_BIV_NORM_DIST(a,b,rho)
Arguments
a: limit for first random variable
b: limit for second random variable
rho: correlation of the two random variables
Description
CUM_BIV_NORM_DIST calculates the probability that two standard normal distributed random variables with correlation rho are respectively each less than a and b.
CUMIPMT
Synopsis
CUMIPMT(rate,nper,pv,start_period,end_period,type)
Arguments
rate: interest rate per period
nper: number of periods
pv: present value
start_period: first period to accumulate for
end_period: last period to accumulate for
type: payment type
Description
CUMIPMT calculates the cumulative interest paid on a loan from start_period to end_period.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
See also
IPMT.
CUMPRINC
Synopsis
CUMPRINC(rate,nper,pv,start_period,end_period,type)
Arguments
rate: interest rate per period
nper: number of periods
pv: present value
start_period: first period to accumulate for
end_period: last period to accumulate for
type: payment type
Description
CUMPRINC calculates the cumulative principal paid on a loan from start_period to end_period.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
See also
PPMT.
DB
Synopsis
DB(cost,salvage,life,period,month)
Arguments
cost: initial cost of asset
salvage: value after depreciation
life: number of periods
period: subject period
month: number of months in first year of depreciation
Description
DB calculates the depreciation of an asset for a given period using the fixed-declining balance method.
DDB
Synopsis
DDB(cost,salvage,life,period,factor)
Arguments
cost: initial cost of asset
salvage: value after depreciation
life: number of periods
period: subject period
factor: factor at which the balance declines
Description
DDB calculates the depreciation of an asset for a given period using the double-declining balance method.
DISC
Synopsis
DISC(settlement,maturity,par,redemption,basis)
Arguments
settlement: settlement date
maturity: maturity date
par: price per $100 face value
redemption: amount received at maturity
basis: calendar basis
Description
DISC calculates the discount rate for a security.
Note
redemption is the redemption value per $100 face value. If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
DOLLARDE
Synopsis
DOLLARDE(fractional_dollar,fraction)
Arguments
fractional_dollar: amount to convert
fraction: denominator
Description
DOLLARDE converts a fractional dollar amount into a decimal amount. This is the inverse of the DOLLARFR function.
See also
DOLLARFR
Synopsis
DOLLARFR(decimal_dollar,fraction)
Arguments
decimal_dollar: amount to convert
fraction: denominator
Description
DOLLARFR converts a decimal dollar amount into a fractional amount which is represented as the digits after the decimal point. For example, 2/8 would be represented as .2 while 3/16 would be represented as .03. This is the inverse of the DOLLARDE function.
See also
DURATION
Synopsis
DURATION(settlement,maturity,coupon,yield,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
coupon: annual coupon rate
yield: annual yield of security
frequency: number of interest payments per year
basis: calendar basis
Description
DURATION calculates the (Macaulay) duration of a security.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
EFFECT
Synopsis
EFFECT(rate,nper)
Arguments
rate: nominal annual interest rate
nper: number of periods used for compounding
Description
EFFECT calculates the effective interest rate using the formula (1+rate/nper)^nper-1.
See also
EURO
Synopsis
EURO(currency)
Arguments
currency: three-letter currency code
Description
EURO calculates the national currency amount corresponding to 1 EUR for any of the national currencies that were replaced by the Euro on its introduction.
Note
currency must be one of ATS (Austria), BEF (Belgium), CYP (Cyprus), DEM (Germany), EEK (Estonia), ESP (Spain), EUR (Euro), FIM (Finland), FRF (France), GRD (Greece), IEP (Ireland), ITL (Italy), LUF (Luxembourg), MTL (Malta), NLG (The Netherlands), PTE (Portugal), SIT (Slovenia), or SKK (Slovakia). This function is not likely to be useful anymore.
See also
EUROCONVERT
Synopsis
EUROCONVERT(n,source,target,full_precision,triangulation_precision)
Arguments
n: amount
source: three-letter source currency code
target: three-letter target currency code
full_precision: whether to provide the full precision; defaults to false
triangulation_precision: number of digits (at least 3) to be rounded to after conversion of the source currency to euro; defaults to no rounding
Description
EUROCONVERT converts n units of currency source to currency target. The rates used are the official ones used on the introduction of the Euro.
Note
If full_precision is true, the result is not rounded; if it false the result is rounded to 0 or 2 decimals depending on the target currency; defaults to false. source and target must be one of the currencies listed for the EURO function. This function is not likely to be useful anymore.
See also
EURO.
FV
Synopsis
FV(rate,nper,pmt,pv,type)
Arguments
rate: effective interest rate per period
nper: number of periods
pmt: payment at each period
pv: present value
type: payment type
Description
FV calculates the future value of pv moved nper periods into the future, assuming a periodic payment of pmt and an interest rate of rate per period.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
See also
PV.
FVSCHEDULE
Synopsis
FVSCHEDULE(principal,schedule)
Arguments
principal: initial value
schedule: range of interest rates
Description
FVSCHEDULE calculates the future value of principal after applying a range of interest rates with compounding.
See also
FV.
G_DURATION
Synopsis
G_DURATION(rate,pv,fv)
Arguments
rate: effective annual interest rate
pv: present value
fv: future value
Description
G_DURATION calculates the number of periods needed for an investment to attain a desired value.
OpenDocument Format (ODF) Compatibility
G_DURATION is the OpenFormula function PDURATION.
INTRATE
Synopsis
INTRATE(settlement,maturity,investment,redemption,basis)
Arguments
settlement: settlement date
maturity: maturity date
investment: amount paid on settlement
redemption: amount received at maturity
basis: calendar basis
Description
INTRATE calculates the interest of a fully vested security.
Note
If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
IPMT
Synopsis
IPMT(rate,per,nper,pv,fv,type)
Arguments
rate: effective annual interest rate
per: period number
nper: number of periods
pv: present value
fv: future value
type: payment type
Description
IPMT calculates the interest part of an annuity's payment for period number per.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
See also
PPMT.
IRR
Synopsis
IRR(values,guess)
Arguments
values: cash flow
guess: an estimate of what the result should be
Description
IRR calculates the internal rate of return of a cash flow with periodic payments. values lists the payments (negative values) and receipts (positive values) for each period.
Note
The optional guess is needed because there can be more than one valid result. It defaults to 10%.
See also
XIRR.
ISPMT
Synopsis
ISPMT(rate,per,nper,pv)
Arguments
rate: effective annual interest rate
per: period number
nper: number of periods
pv: present value
Description
ISPMT calculates the interest payment for period number per.
See also
PV.
MDURATION
Synopsis
MDURATION(settlement,maturity,coupon,yield,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
coupon: annual coupon rate
yield: annual yield of security
frequency: number of interest payments per year
basis: calendar basis
Description
MDURATION calculates the modified (Macaulay) duration of a security.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
MIRR
Synopsis
MIRR(values,finance_rate,reinvest_rate)
Arguments
values: cash flow
finance_rate: interest rate for financing cost
reinvest_rate: interest rate for reinvestments
Description
MIRR calculates the modified internal rate of return of a periodic cash flow.
NOMINAL
Synopsis
NOMINAL(rate,nper)
Arguments
rate: effective annual interest rate
nper: number of periods used for compounding
Description
NOMINAL calculates the nominal interest rate from the effective rate.
See also
NPER
Synopsis
NPER(rate,pmt,pv,fv,type)
Arguments
rate: effective annual interest rate
pmt: payment at each period
pv: present value
fv: future value
type: payment type
Description
NPER calculates the number of periods of an investment based on periodic constant payments and a constant interest rate.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
NPV
Synopsis
NPV(rate,value1,value2,…)
Arguments
rate: effective interest rate per period
value1: cash flow for period 1
value2: cash flow for period 2
Description
NPV calculates the net present value of a cash flow.
See also
PV.
ODDFPRICE
Synopsis
ODDFPRICE(settlement,maturity,issue,first_interest,rate,yield,redemption,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
issue: date of issue
first_interest: first interest date
rate: nominal annual interest rate
yield: annual yield of security
redemption: amount received at maturity
frequency: number of interest payments per year
basis: calendar basis
Description
ODDFPRICE calculates the price per $100 face value of a security that pays periodic interest, but has an odd first period.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
ODDFYIELD
Synopsis
ODDFYIELD(settlement,maturity,issue,first_interest,rate,price,redemption,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
issue: date of issue
first_interest: first interest date
rate: nominal annual interest rate
price: price of security
redemption: amount received at maturity
frequency: number of interest payments per year
basis: calendar basis
Description
ODDFYIELD calculates the yield of a security that pays periodic interest, but has an odd first period.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
ODDLPRICE
Synopsis
ODDLPRICE(settlement,maturity,last_interest,rate,yield,redemption,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
last_interest: last interest date
rate: nominal annual interest rate
yield: annual yield of security
redemption: amount received at maturity
frequency: number of interest payments per year
basis: calendar basis
Description
ODDLPRICE calculates the price per $100 face value of a security that pays periodic interest, but has an odd last period.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
ODDLYIELD
Synopsis
ODDLYIELD(settlement,maturity,last_interest,rate,price,redemption,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
last_interest: last interest date
rate: nominal annual interest rate
price: price of security
redemption: amount received at maturity
frequency: number of interest payments per year
basis: calendar basis
Description
ODDLYIELD calculates the yield of a security that pays periodic interest, but has an odd last period.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
OPT_2_ASSET_CORRELATION
Synopsis
OPT_2_ASSET_CORRELATION(call_put_flag,spot1,spot2,strike1,strike2,time,cost_of_carry1,cost_of_carry2,rate,volatility1,volatility2,rho)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot1: spot price of the underlying asset of the first option
spot2: spot price of the underlying asset of the second option
strike1: strike prices of the first option
strike2: strike prices of the second option
time: time to maturity in years
cost_of_carry1: net cost of holding the underlying asset of the first option (for common stocks, the risk free rate less the dividend yield)
cost_of_carry2: net cost of holding the underlying asset of the second option (for common stocks, the risk free rate less the dividend yield)
rate: annualized risk-free interest rate
volatility1: annualized volatility in price of the underlying asset of the first option
volatility2: annualized volatility in price of the underlying asset of the second option
rho: correlation between the two underlying assets
Description
OPT_2_ASSET_CORRELATION models the theoretical price of options on 2 assets with correlation rho. The payoff for a call is max(spot2 - strike2,0) if spot1 > strike1 or 0 otherwise. The payoff for a put is max (strike2 - spot2, 0) if spot1 < strike1 or 0 otherwise.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_AMER_EXCHANGE
Synopsis
OPT_AMER_EXCHANGE(spot1,spot2,qty1,qty2,time,rate,cost_of_carry1,cost_of_carry2,volatility1,volatility2,rho)
Arguments
spot1: spot price of asset 1
spot2: spot price of asset 2
qty1: quantity of asset 1
qty2: quantity of asset 2
time: time to maturity in years
rate: annualized risk-free interest rate
cost_of_carry1: net cost of holding asset 1 (for common stocks, the risk free rate less the dividend yield)
cost_of_carry2: net cost of holding asset 2 (for common stocks, the risk free rate less the dividend yield)
volatility1: annualized volatility in price of asset 1
volatility2: annualized volatility in price of asset 2
rho: correlation between the prices of the two assets
Description
OPT_AMER_EXCHANGE models the theoretical price of an American option to exchange one asset with quantity qty2 and spot price spot2 for another with quantity qty1 and spot price spot1.
See also
OPT_EURO_EXCHANGE, OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_BAW_AMER
Synopsis
OPT_BAW_AMER(call_put_flag,spot,strike,time,rate,cost_of_carry,volatility)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in days
rate: annualized risk-free interest rate
cost_of_carry: net cost of holding the underlying asset
volatility: annualized volatility of the asset
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_BINOMIAL
Synopsis
OPT_BINOMIAL(amer_euro_flag,call_put_flag,num_time_steps,spot,strike,time,rate,volatility,cost_of_carry)
Arguments
amer_euro_flag: 'a' for an American style option or 'e' for a European style option
call_put_flag: 'c' for a call and 'p' for a put
num_time_steps: number of time steps used in the valuation
spot: spot price
strike: strike price
time: time to maturity in years
rate: annualized risk-free interest rate
volatility: annualized volatility of the asset
cost_of_carry: net cost of holding the underlying asset
Note
A larger num_time_steps yields greater accuracy but OPT_BINOMIAL is slower to calculate.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_BJER_STENS
Synopsis
OPT_BJER_STENS(call_put_flag,spot,strike,time,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in days
rate: annualized risk-free interest rate
volatility: annualized volatility of the asset
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_BS
Synopsis
OPT_BS(call_put_flag,spot,strike,time,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in years
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_BS uses the Black-Scholes model to calculate the price of a European option struck at strike on an asset with spot price spot.
Note
The returned value will be expressed in the same units as strike and spot.
See also
OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_VEGA, OPT_BS_GAMMA.
OPT_BS_CARRYCOST
Synopsis
OPT_BS_CARRYCOST(call_put_flag,spot,strike,time,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in years
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_BS_CARRYCOST uses the Black-Scholes model to calculate the 'elasticity' of a European option struck at strike on an asset with spot price spot. The elasticity of an option is the rate of change of its price with respect to its cost_of_carry.
Note
Elasticity is expressed as the rate of change of the option value, per 100% volatility.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_BS_DELTA
Synopsis
OPT_BS_DELTA(call_put_flag,spot,strike,time,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in years
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_BS_DELTA uses the Black-Scholes model to calculate the 'delta' of a European option struck at strike on an asset with spot price spot.
Note
The returned value will be expressed in the same units as strike and spot.
See also
OPT_BS, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_VEGA, OPT_BS_GAMMA.
OPT_BS_GAMMA
Synopsis
OPT_BS_GAMMA(spot,strike,time,rate,volatility,cost_of_carry)
Arguments
spot: spot price
strike: strike price
time: time to maturity in years
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_BS_GAMMA uses the Black-Scholes model to calculate the 'gamma' of a European option struck at strike on an asset with spot price spot. The gamma of an option is the second derivative of its price with respect to the price of the underlying asset.
Note
Gamma is expressed as the rate of change of delta per unit change in spot. Gamma is the same for calls and puts.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_VEGA.
OPT_BS_RHO
Synopsis
OPT_BS_RHO(call_put_flag,spot,strike,time,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in years
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_BS_RHO uses the Black-Scholes model to calculate the 'rho' of a European option struck at strike on an asset with spot price spot. The rho of an option is the rate of change of its price with respect to the risk free interest rate.
Note
Rho is expressed as the rate of change of the option value, per 100% change in rate.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_THETA, OPT_BS_VEGA, OPT_BS_GAMMA.
OPT_BS_THETA
Synopsis
OPT_BS_THETA(call_put_flag,spot,strike,time,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in years
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_BS_THETA uses the Black-Scholes model to calculate the 'theta' of a European option struck at strike on an asset with spot price spot. The theta of an option is the rate of change of its price with respect to time to expiry.
Note
Theta is expressed as the negative of the rate of change of the option value, per 365.25 days.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_VEGA, OPT_BS_GAMMA.
OPT_BS_VEGA
Synopsis
OPT_BS_VEGA(spot,strike,time,rate,volatility,cost_of_carry)
Arguments
spot: spot price
strike: strike price
time: time to maturity in years
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_BS_VEGA uses the Black-Scholes model to calculate the 'vega' of a European option struck at strike on an asset with spot price spot. The vega of an option is the rate of change of its price with respect to volatility.
Note
Vega is the same for calls and puts. Vega is expressed as the rate of change of option value, per 100% volatility.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_COMPLEX_CHOOSER
Synopsis
OPT_COMPLEX_CHOOSER(spot,strike_call,strike_put,time,time_call,time_put,rate,cost_of_carry,volatility)
Arguments
spot: spot price
strike_call: strike price, if exercised as a call option
strike_put: strike price, if exercised as a put option
time: time in years until the holder chooses a put or a call option
time_call: time in years to maturity of the call option if chosen
time_put: time in years to maturity of the put option if chosen
rate: annualized risk-free interest rate
cost_of_carry: net cost of holding the underlying asset
volatility: annualized volatility of the asset in percent for the period through to the exercise date
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_EURO_EXCHANGE
Synopsis
OPT_EURO_EXCHANGE(spot1,spot2,qty1,qty2,time,rate,cost_of_carry1,cost_of_carry2,volatility1,volatility2,rho)
Arguments
spot1: spot price of asset 1
spot2: spot price of asset 2
qty1: quantity of asset 1
qty2: quantity of asset 2
time: time to maturity in years
rate: annualized risk-free interest rate
cost_of_carry1: net cost of holding asset 1 (for common stocks, the risk free rate less the dividend yield)
cost_of_carry2: net cost of holding asset 2 (for common stocks, the risk free rate less the dividend yield)
volatility1: annualized volatility in price of asset 1
volatility2: annualized volatility in price of asset 2
rho: correlation between the prices of the two assets
Description
OPT_EURO_EXCHANGE models the theoretical price of a European option to exchange one asset with quantity qty2 and spot price spot2 for another with quantity qty1 and spot price spot1.
See also
OPT_AMER_EXCHANGE, OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_EXEC
Synopsis
OPT_EXEC(call_put_flag,spot,strike,time,rate,volatility,cost_of_carry,lambda)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in days
rate: annualized risk-free interest rate
volatility: annualized volatility of the asset
cost_of_carry: net cost of holding the underlying asset
lambda: jump rate for executives
Note
The model assumes executives forfeit their options if they leave the company.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_EXTENDIBLE_WRITER
Synopsis
OPT_EXTENDIBLE_WRITER(call_put_flag,spot,strike1,strike2,time1,time2,rate,cost_of_carry,volatility)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike1: strike price at which the option is struck
strike2: strike price at which the option is re-struck if out of the money at time1
time1: initial maturity of the option in years
time2: extended maturity in years if chosen
rate: annualized risk-free interest rate
cost_of_carry: net cost of holding the underlying asset
volatility: annualized volatility of the asset
Description
OPT_EXTENDIBLE_WRITER models the theoretical price of extendible writer options. These are options that have their maturity extended to time2 if the option is out of the money at time1.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_FIXED_STRK_LKBK
Synopsis
OPT_FIXED_STRK_LKBK(call_put_flag,spot,spot_min,spot_max,strike,time,rate,cost_of_carry,volatility)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
spot_min: minimum spot price of the underlying asset so far observed
spot_max: maximum spot price of the underlying asset so far observed
strike: strike price
time: time to maturity in years
rate: annualized risk-free interest rate
cost_of_carry: net cost of holding the underlying asset
volatility: annualized volatility of the asset
Description
OPT_FIXED_STRK_LKBK determines the theoretical price of a fixed-strike lookback option where the holder of the option may exercise on expiry at the most favourable price observed during the options life of the underlying asset.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_FLOAT_STRK_LKBK
Synopsis
OPT_FLOAT_STRK_LKBK(call_put_flag,spot,spot_min,spot_max,time,rate,cost_of_carry,volatility)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
spot_min: minimum spot price of the underlying asset so far observed
spot_max: maximum spot price of the underlying asset so far observed
time: time to maturity in years
rate: annualized risk-free interest rate
cost_of_carry: net cost of holding the underlying asset
volatility: annualized volatility of the asset
Description
OPT_FLOAT_STRK_LKBK determines the theoretical price of a floating-strike lookback option where the holder of the option may exercise on expiry at the most favourable price observed during the options life of the underlying asset.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_FORWARD_START
Synopsis
OPT_FORWARD_START(call_put_flag,spot,alpha,time_start,time,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
alpha: fraction setting the strike price at the future date time_start
time_start: time until the option starts in days
time: time to maturity in days
rate: annualized risk-free interest rate
volatility: annualized volatility of the asset
cost_of_carry: net cost of holding the underlying asset
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_FRENCH
Synopsis
OPT_FRENCH(call_put_flag,spot,strike,time,ttime,rate,volatility,cost_of_carry)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: ratio of the number of calendar days to exercise and the number of calendar days in the year
ttime: ratio of the number of trading days to exercise and the number of trading days in the year
rate: risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
cost_of_carry: net cost of holding the underlying asset (for common stocks, the risk free rate less the dividend yield), defaults to 0
Description
OPT_FRENCH values the theoretical price of a European option adjusted for trading day volatility, struck at strike on an asset with spot price spot.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_GARMAN_KOHLHAGEN
Synopsis
OPT_GARMAN_KOHLHAGEN(call_put_flag,spot,strike,time,domestic_rate,foreign_rate,volatility)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: number of days to exercise
domestic_rate: domestic risk-free interest rate to the exercise date in percent
foreign_rate: foreign risk-free interest rate to the exercise date in percent
volatility: annualized volatility of the asset in percent for the period through to the exercise date
Description
OPT_GARMAN_KOHLHAGEN values the theoretical price of a European currency option struck at strike on an asset with spot price spot.
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_JUMP_DIFF
Synopsis
OPT_JUMP_DIFF(call_put_flag,spot,strike,time,rate,volatility,lambda,gamma)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time: time to maturity in years
rate: the annualized rate of interest
volatility: annualized volatility of the asset in percent for the period through to the exercise date
lambda: expected number of 'jumps' per year
gamma: proportion of volatility explained by the 'jumps'
Description
OPT_JUMP_DIFF models the theoretical price of an option according to the Jump Diffusion process (Merton).
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_MILTERSEN_SCHWARTZ
Synopsis
OPT_MILTERSEN_SCHWARTZ(call_put_flag,p_t,f_t,strike,t1,t2,v_s,v_e,v_f,rho_se,rho_sf,rho_ef,kappa_e,kappa_f)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
p_t: zero coupon bond with expiry at option maturity
f_t: futures price
strike: strike price
t1: time to maturity of the option
t2: time to maturity of the underlying commodity futures contract
v_s: volatility of the spot commodity price
v_e: volatility of the future convenience yield
v_f: volatility of the forward rate of interest
rho_se: correlation between the spot commodity price and the convenience yield
rho_sf: correlation between the spot commodity price and the forward interest rate
rho_ef: correlation between the forward interest rate and the convenience yield
kappa_e: speed of mean reversion of the convenience yield
kappa_f: speed of mean reversion of the forward interest rate
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_ON_OPTIONS
Synopsis
OPT_ON_OPTIONS(type_flag,spot,strike1,strike2,time1,time2,rate,cost_of_carry,volatility)
Arguments
type_flag: 'cc' for calls on calls, 'cp' for calls on puts, and so on for 'pc', and 'pp'
spot: spot price
strike1: strike price at which the option being valued is struck
strike2: strike price at which the underlying option is struck
time1: time in years to maturity of the option
time2: time in years to the maturity of the underlying option
rate: annualized risk-free interest rate
cost_of_carry: net cost of holding the underlying asset of the underlying option
volatility: annualized volatility in price of the underlying asset of the underlying option
Note
For common stocks, cost_of_carry is the risk free rate less the dividend yield. time2 ≥ time1
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_RGW
Synopsis
OPT_RGW(spot,strike,time_payout,time_exp,rate,d,volatility)
Arguments
spot: spot price
strike: strike price
time_payout: time to dividend payout
time_exp: time to expiration
rate: annualized interest rate
d: amount of the dividend to be paid expressed in currency
volatility: annualized volatility of the asset in percent for the period through to the exercise date
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_SIMPLE_CHOOSER
Synopsis
OPT_SIMPLE_CHOOSER(call_put_flag,spot,strike,time1,time2,cost_of_carry,volatility)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
time1: time in years until the holder chooses a put or a call option
time2: time in years until the chosen option expires
cost_of_carry: net cost of holding the underlying asset
volatility: annualized volatility of the asset
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_SPREAD_APPROX
Synopsis
OPT_SPREAD_APPROX(call_put_flag,fut_price1,fut_price2,strike,time,rate,volatility1,volatility2,rho)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
fut_price1: price of the first futures contract
fut_price2: price of the second futures contract
strike: strike price
time: time to maturity in years
rate: annualized risk-free interest rate
volatility1: annualized volatility in price of the first underlying futures contract
volatility2: annualized volatility in price of the second underlying futures contract
rho: correlation between the two futures contracts
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
OPT_TIME_SWITCH
Synopsis
OPT_TIME_SWITCH(call_put_flag,spot,strike,a,time,m,dt,rate,cost_of_carry,volatility)
Arguments
call_put_flag: 'c' for a call and 'p' for a put
spot: spot price
strike: strike price
a: amount received for each time period
time: time to maturity in years
m: number of time units the option has already met the condition
dt: agreed upon discrete time period expressed as a fraction of a year
rate: annualized risk-free interest rate
cost_of_carry: net cost of holding the underlying asset
volatility: annualized volatility of the asset
Description
OPT_TIME_SWITCH models the theoretical price of time switch options. (Pechtl 1995). The holder receives a * dt for each period that the asset price was greater than strike (for a call) or below it (for a put).
See also
OPT_BS, OPT_BS_DELTA, OPT_BS_RHO, OPT_BS_THETA, OPT_BS_GAMMA.
PMT
Synopsis
PMT(rate,nper,pv,fv,type)
Arguments
rate: effective annual interest rate
nper: number of periods
pv: present value
fv: future value
type: payment type
Description
PMT calculates the payment amount for an annuity.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
PPMT
Synopsis
PPMT(rate,per,nper,pv,fv,type)
Arguments
rate: effective annual interest rate
per: period number
nper: number of periods
pv: present value
fv: future value
type: payment type
Description
PPMT calculates the principal part of an annuity's payment for period number per.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
See also
IPMT.
PRICE
Synopsis
PRICE(settlement,maturity,rate,yield,redemption,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
rate: nominal annual interest rate
yield: annual yield of security
redemption: amount received at maturity
frequency: number of interest payments per year
basis: calendar basis
Description
PRICE calculates the price per $100 face value of a security that pays periodic interest.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
PRICEDISC
Synopsis
PRICEDISC(settlement,maturity,discount,redemption,basis)
Arguments
settlement: settlement date
maturity: maturity date
discount: annual rate at which to discount
redemption: amount received at maturity
basis: calendar basis
Description
PRICEDISC calculates the price per $100 face value of a bond that does not pay interest at maturity.
Note
If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
PRICEMAT
Synopsis
PRICEMAT(settlement,maturity,issue,discount,yield,basis)
Arguments
settlement: settlement date
maturity: maturity date
issue: date of issue
discount: annual rate at which to discount
yield: annual yield of security
basis: calendar basis
Description
PRICEMAT calculates the price per $100 face value of a bond that pays interest at maturity.
Note
If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
PV
Synopsis
PV(rate,nper,pmt,fv,type)
Arguments
rate: effective interest rate per period
nper: number of periods
pmt: payment at each period
fv: future value
type: payment type
Description
PV calculates the present value of fv which is nper periods into the future, assuming a periodic payment of pmt and an interest rate of rate per period.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
See also
FV.
RATE
Synopsis
RATE(nper,pmt,pv,fv,type,guess)
Arguments
nper: number of periods
pmt: payment at each period
pv: present value
fv: future value
type: payment type
guess: an estimate of what the result should be
Description
RATE calculates the rate of return.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period. The optional guess is needed because there can be more than one valid result. It defaults to 10%.
RECEIVED
Synopsis
RECEIVED(settlement,maturity,investment,rate,basis)
Arguments
settlement: settlement date
maturity: maturity date
investment: amount paid on settlement
rate: nominal annual interest rate
basis: calendar basis
Description
RECEIVED calculates the amount to be received when a security matures.
Note
If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
See also
RRI
Synopsis
RRI(p,pv,fv)
Arguments
p: number of periods
pv: present value
fv: future value
Description
RRI determines an equivalent interest rate for an investment that increases in value. The interest is compounded after each complete period.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period. Note that p need not be an integer but for fractional value the calculated rate is only approximate.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
SLN
Synopsis
SLN(cost,salvage,life)
Arguments
cost: initial cost of asset
salvage: value after depreciation
life: number of periods
Description
SLN calculates the depreciation of an asset using the straight-line method.
SYD
Synopsis
SYD(cost,salvage,life,period)
Arguments
cost: initial cost of asset
salvage: value after depreciation
life: number of periods
period: subject period
Description
SYD calculates the depreciation of an asset using the sum-of-years method.
TBILLEQ
Synopsis
TBILLEQ(settlement,maturity,discount)
Arguments
settlement: settlement date
maturity: maturity date
discount: annual rate at which to discount
Description
TBILLEQ calculates the bond-equivalent yield for a treasury bill.
See also
TBILLPRICE
Synopsis
TBILLPRICE(settlement,maturity,discount)
Arguments
settlement: settlement date
maturity: maturity date
discount: annual rate at which to discount
Description
TBILLPRICE calculates the price per $100 face value for a treasury bill.
See also
TBILLYIELD
Synopsis
TBILLYIELD(settlement,maturity,price)
Arguments
settlement: settlement date
maturity: maturity date
price: price
Description
TBILLYIELD calculates the yield of a treasury bill.
See also
VDB
Synopsis
VDB(cost,salvage,life,start_period,end_period,factor,no_switch)
Arguments
cost: initial cost of asset
salvage: value after depreciation
life: number of periods
start_period: first period to accumulate for
end_period: last period to accumulate for
factor: factor at which the balance declines
no_switch: do not switch to straight-line depreciation
Description
VDB calculates the depreciation of an asset for a given period range using the variable-rate declining balance method.
Note
If no_switch is FALSE, the calculation switches to straight-line depreciation when depreciation is greater than the declining balance calculation.
XIRR
Synopsis
XIRR(values,dates,guess)
Arguments
values: cash flow
dates: dates of cash flow
guess: an estimate of what the result should be
Description
XIRR calculates the annualized internal rate of return of a cash flow at arbitrary points in time. values lists the payments (negative values) and receipts (positive values) with one value for each entry in dates.
Note
The optional guess is needed because there can be more than one valid result. It defaults to 10%.
See also
IRR.
XNPV
Synopsis
XNPV(rate,values,dates)
Arguments
rate: effective annual interest rate
values: cash flow
dates: dates of cash flow
Description
XNPV calculates the net present value of a cash flow at irregular times.
Note
If type is 0, the default, payment is at the end of each period. If type is 1, payment is at the beginning of each period.
See also
NPV.
YIELD
Synopsis
YIELD(settlement,maturity,rate,price,redemption,frequency,basis)
Arguments
settlement: settlement date
maturity: maturity date
rate: nominal annual interest rate
price: price of security
redemption: amount received at maturity
frequency: number of interest payments per year
basis: calendar basis
Description
YIELD calculates the yield of a security that pays periodic interest.
Note
frequency may be 1 (annual), 2 (semi-annual), or 4 (quarterly). If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
YIELDDISC
Synopsis
YIELDDISC(settlement,maturity,price,redemption,basis)
Arguments
settlement: settlement date
maturity: maturity date
price: price of security
redemption: amount received at maturity
basis: calendar basis
Description
YIELDDISC calculates the yield of a discounted security.
Note
If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
YIELDMAT
Synopsis
YIELDMAT(settlement,maturity,issue,rate,price,basis)
Arguments
settlement: settlement date
maturity: maturity date
issue: date of issue
rate: nominal annual interest rate
price: price of security
basis: calendar basis
Description
YIELDMAT calculates the yield of a security for which the interest is paid at maturity date.
Note
If basis is 0, then the US 30/360 method is used. If basis is 1, then actual number of days is used. If basis is 2, then actual number of days is used within a month, but years are considered only 360 days. If basis is 3, then actual number of days is used within a month, but years are always considered 365 days. If basis is 4, then the European 30/360 method is used.
A.8. Gnumeric
- GNUMERIC_VERSION — the current version of Gnumeric
A.9. Information
- CELL — information of type about cell
- COUNTBLANK — the number of blank cells in range
- ERROR — the error with the given name
- ERROR.TYPE — the type of error
- EXPRESSION — expression in cell as a string
- GET.FORMULA — the formula in cell as a string
- GET.LINK — the target of the hyperlink attached to cell as a string
- GETENV — the value of execution environment variable name
- INFO — information about the current operating environment according to type
- ISBLANK — TRUE if value is blank
- ISERR — TRUE if value is any error value except #N/A
- ISERROR — TRUE if value is any error value
- ISEVEN — TRUE if n is even
- ISFORMULA — TRUE if cell contains a formula
- ISLOGICAL — TRUE if value is a logical value
- ISNA — TRUE if value is the #N/A error value
- ISNONTEXT — TRUE if value is not text
- ISNUMBER — TRUE if value is a number
- ISODD — TRUE if n is odd
- ISREF — TRUE if value is a reference
- ISTEXT — TRUE if value is text
- N — text converted to a number
- NA — the error value #N/A
- TYPE — a number indicating the data type of value
CELL
Synopsis
CELL(type,cell)
Arguments
type: string specifying the type of information requested
cell: cell reference
Description
type specifies the type of information you want to obtain:
address Returns the given cell reference as text.
col Returns the number of the column in cell.
color Returns 0.
contents Returns the contents of the cell in cell.
column Returns the number of the column in cell.
columnwidth Returns the column width.
coord Returns the absolute address of cell.
datatype same as type
filename Returns the name of the file of cell.
format Returns the code of the format of the cell.
formulatype same as type
locked Returns 1 if cell is locked.
parentheses Returns 1 if cell contains a negative value
and its format displays it with parentheses.
prefix Returns a character indicating the horizontal
alignment of cell.
prefixcharacter same as prefix
protect Returns 1 if cell is locked.
row Returns the number of the row in cell.
sheetname Returns the name of the sheet of cell.
type Returns "l" if cell contains a string,
"v" if it contains some other value, and
"b" if cell is blank.
value Returns the contents of the cell in cell.
width Returns the column width.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
COUNTBLANK
Synopsis
COUNTBLANK(range)
Arguments
range: a cell range
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ERROR.TYPE
Synopsis
ERROR.TYPE(error)
Arguments
error: an error
Description
ERROR.TYPE returns an error number corresponding to the given error value. The error numbers for error values are:
#DIV/0! 2
#VALUE! 3
#REF! 4
#NAME? 5
#NUM! 6
#N/A 7
Microsoft Excel Compatibility
This function is Excel compatible.
See also
EXPRESSION
Synopsis
EXPRESSION(cell)
Arguments
cell: a cell reference
Note
If cell contains no expression, EXPRESSION returns empty.
See also
TEXT.
GET.FORMULA
Synopsis
GET.FORMULA(cell)
Arguments
cell: the referenced cell
OpenDocument Format (ODF) Compatibility
GET.FORMULA is the OpenFormula function FORMULA.
See also
GET.LINK
Synopsis
GET.LINK(cell)
Arguments
cell: the referenced cell
Note
The value return is not updated automatically when the link attached to cell changes but requires a recalculation.
See also
GETENV
Synopsis
GETENV(name)
Arguments
name: the name of the environment variable
Note
If a variable called name does not exist, #N/A will be returned. Variable names are case sensitive.
INFO
Synopsis
INFO(type)
Arguments
type: string giving the type of information requested
Description
INFO returns information about the current operating environment according to type:
memavail Returns the amount of memory available, bytes.
memused Returns the amount of memory used (bytes).
numfile Returns the number of active worksheets.
osversion Returns the operating system version.
recalc Returns the recalculation mode (automatic).
release Returns the version of Gnumeric as text.
system Returns the name of the environment.
totmem Returns the amount of total memory available.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
CELL.
ISBLANK
Synopsis
ISBLANK(value)
Arguments
value: a value
Description
This function checks if a value is blank. Empty cells are blank, but empty strings are not.
Microsoft Excel Compatibility
This function is Excel compatible.
ISERR
Synopsis
ISERR(value)
Arguments
value: a value
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ISERROR
Synopsis
ISERROR(value)
Arguments
value: a value
Microsoft Excel Compatibility
This function is Excel compatible.
ISEVEN
Synopsis
ISEVEN(n)
Arguments
n: number
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ISFORMULA
Synopsis
ISFORMULA(cell)
Arguments
cell: the referenced cell
OpenDocument Format (ODF) Compatibility
ISFORMULA is OpenFormula compatible.
See also
ISLOGICAL
Synopsis
ISLOGICAL(value)
Arguments
value: a value
Description
This function checks if a value is either TRUE or FALSE.
Microsoft Excel Compatibility
This function is Excel compatible.
ISNA
Synopsis
ISNA(value)
Arguments
value: a value
Microsoft Excel Compatibility
This function is Excel compatible.
See also
NA.
ISNONTEXT
Synopsis
ISNONTEXT(value)
Arguments
value: a value
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ISNUMBER
Synopsis
ISNUMBER(value)
Arguments
value: a value
Description
This function checks if a value is a number. Neither TRUE nor FALSE are numbers for this purpose.
Microsoft Excel Compatibility
This function is Excel compatible.
ISODD
Synopsis
ISODD(n)
Arguments
n: number
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ISREF
Synopsis
ISREF(value,…)
Arguments
value: a value
Description
This function checks if a value is a cell reference.
Microsoft Excel Compatibility
This function is Excel compatible.
ISTEXT
Synopsis
ISTEXT(value)
Arguments
value: a value
Microsoft Excel Compatibility
This function is Excel compatible.
See also
N
Synopsis
N(text)
Arguments
text: string
Note
If text contains non-numerical text, 0 is returned.
Microsoft Excel Compatibility
This function is Excel compatible.
NA
Synopsis
NA()Microsoft Excel Compatibility
This function is Excel compatible.
See also
ISNA.
A.10. Logic
AND
Synopsis
AND(b0,b1,…)
Arguments
b0: logical value
b1: logical value
Description
AND calculates the logical conjunction of its arguments b0,b1,...
Note
If an argument is numerical, zero is considered FALSE and anything else TRUE. Strings and empty values are ignored. If no logical values are provided, then the error #VALUE! is returned. This function is strict: if any argument is an error, the result will be the first such error.
Microsoft Excel Compatibility
This function is Excel compatible.
FALSE
Synopsis
FALSE()Description
FALSE returns the value FALSE.
Microsoft Excel Compatibility
This function is Excel compatible.
IF
Synopsis
IF(cond,trueval,falseval)
Arguments
cond: condition
trueval: value to use if condition is true
falseval: value to use if condition is false
Description
This function first evaluates the condition. If the result is true, it will then evaluate and return the second argument. Otherwise, it will evaluate and return the last argument.
IFERROR
Synopsis
IFERROR(x,y)
Arguments
x: value to test for error
y: alternate value
Description
This function returns the first value, unless that is an error, in which case it returns the second.
IFNA
Synopsis
IFNA(x,y)
Arguments
x: value to test for #N/A error
y: alternate value
Description
This function returns the first value, unless that is #N/A, in which case it returns the second.
IFS
Synopsis
IFS(cond1,value1,cond2,value2,…)
Arguments
cond1: condition
value1: value if condition1 is true
cond2: condition
value2: value if condition2 is true
Description
This function returns the value after the first true conditional. If no conditional is true, #VALUE! is returned.
See also
IF.
NOT
Synopsis
NOT(b)
Arguments
b: logical value
Description
NOT calculates the logical negation of its argument.
Note
If the argument is numerical, zero is considered FALSE and anything else TRUE. Strings and empty values are ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
OR
Synopsis
OR(b0,b1,…)
Arguments
b0: logical value
b1: logical value
Description
OR calculates the logical disjunction of its arguments b0,b1,...
Note
If an argument is numerical, zero is considered FALSE and anything else TRUE. Strings and empty values are ignored. If no logical values are provided, then the error #VALUE! is returned. This function is strict: if any argument is an error, the result will be the first such error.
Microsoft Excel Compatibility
This function is Excel compatible.
SWITCH
Synopsis
SWITCH(ref,choice1,value1,choice2,value2,…)
Arguments
ref: value
choice1: first choice value
value1: first result value
choice2: second choice value
value2: second result value
Description
This function compares the reference value, ref, against the choice values, choice1 etc., and returns the corresponding result value when it finds a match. The choices may be followed by a default value to use. If there are no choices that match and no default value, #N/A is return.
TRUE
Synopsis
TRUE()Description
TRUE returns the value TRUE.
Microsoft Excel Compatibility
This function is Excel compatible.
XOR
Synopsis
XOR(b0,b1,…)
Arguments
b0: logical value
b1: logical value
Description
XOR calculates the logical exclusive disjunction of its arguments b0,b1,...
Note
If an argument is numerical, zero is considered FALSE and anything else TRUE. Strings and empty values are ignored. If no logical values are provided, then the error #VALUE! is returned. This function is strict: if any argument is an error, the result will be the first such error.
A.11. Lookup
- ADDRESS — cell address as text
- AREAS — number of areas in reference
- ARRAY — vertical array of the arguments
- CHOOSE — the (index+1)th argument
- COLUMN — vector of column numbers
- COLUMNNUMBER — column number for the given column called name
- COLUMNS — number of columns in reference
- FLIP — matrix flipped
- HLOOKUP — search the first row of range for value
- HYPERLINK — second or first arguments
- INDEX — reference to a cell in the given array
- INDIRECT — contents of the cell pointed to by the ref_text string
- LOOKUP — contents of vector2 at the corresponding location to value in vector1
- MATCH — the index of seek in vector
- OFFSET — an offset cell range
- ROW — vector of row numbers
- ROWS — number of rows in reference
- SHEET — sheet number of reference
- SHEETS — number of sheets in reference
- SORT — sorted list of numbers as vertical array
- TRANSPOSE — the transpose of matrix
- VLOOKUP — search the first column of range for value
ADDRESS
Synopsis
ADDRESS(row_num,col_num,abs_num,a1,text)
Arguments
row_num: row number
col_num: column number
abs_num: 1 for an absolute, 2 for a row absolute and column relative, 3 for a row relative and column absolute, and 4 for a relative reference; defaults to 1
a1: if TRUE, an A1-style reference is provided, otherwise an R1C1-style reference; defaults to TRUE
text: name of the worksheet, defaults to no sheet
Note
If row_num or col_num is less than one, ADDRESS returns #VALUE! If abs_num is greater than 4 ADDRESS returns #VALUE!
See also
CHOOSE
Synopsis
CHOOSE(index,value1,value2,…)
Arguments
index: positive number
value1: first value
value2: second value
Description
CHOOSE returns its (index+1)th argument.
Note
index is truncated to an integer. If index < 1 or the truncated index > number of values, CHOOSE returns #VALUE!
See also
IF.
COLUMN
Synopsis
COLUMN(x)
Arguments
x: reference, defaults to the position of the current expression
Description
COLUMN function returns a Nx1 array containing the sequence of integers from the first column to the last column of x.
Note
If x is neither an array nor a reference nor a range, returns #VALUE!
COLUMNNUMBER
Synopsis
COLUMNNUMBER(name)
Arguments
name: column name such as "IV"
Note
If name is invalid, COLUMNNUMBER returns #VALUE!
See also
COLUMNS
Synopsis
COLUMNS(reference)
Arguments
reference: array or area
Note
If reference is neither an array nor a reference nor a range, COLUMNS returns #VALUE!
FLIP
Synopsis
FLIP(matrix,vertical)
Arguments
matrix: range
vertical: if true, matrix is flipped vertically, otherwise horizontally; defaults to TRUE
See also
HLOOKUP
Synopsis
HLOOKUP(value,range,row,approximate,as_index)
Arguments
value: search value
range: range to search
row: 1-based row offset indicating the return values
approximate: if false, an exact match of value must be found; defaults to TRUE
as_index: if true, the 0-based column offset is returned; defaults to FALSE
Description
HLOOKUP function finds the row in range that has a first cell similar to value. If approximate is not true it finds the column with an exact equality. If approximate is true, it finds the last column with first value less than or equal to value. If as_index is true the 0-based column offset is returned.
Note
If approximate is true, then the values must be sorted in order of ascending value. HLOOKUP returns #REF! if row falls outside range.
See also
HYPERLINK
Synopsis
HYPERLINK(link_location,label)
Arguments
link_location: string
label: string, optional
Description
HYPERLINK function currently returns its 2nd argument, or if that is omitted the 1st argument.
INDEX
Synopsis
INDEX(array,row,col,area,…)
Arguments
array: cell or inline array
row: desired row, defaults to 1
col: desired column, defaults to 1
area: from which area to select a cell, defaults to 1
Description
INDEX gives a reference to a cell in the given array. The cell is selected by row and col, which count the rows and columns in the array.
Note
If the reference falls outside the range of array, INDEX returns #REF!
INDIRECT
Synopsis
INDIRECT(ref_text,format)
Arguments
ref_text: textual reference
format: if true, ref_text is given in A1-style, otherwise it is given in R1C1 style; defaults to true
Note
If ref_text is not a valid reference in the style determined by format, INDIRECT returns #REF!
LOOKUP
Synopsis
LOOKUP(value,vector1,vector2)
Arguments
value: value to look up
vector1: range to search:
vector2: range of return values
Description
If vector1 has more rows than columns, LOOKUP searches the first row of vector1, otherwise the first column. If vector2 is omitted the return value is taken from the last row or column of vector1.
Note
If LOOKUP can't find value it uses the largest value less than value. The data must be sorted. If value is smaller than the first value it returns #N/A. If the corresponding location does not exist in vector2, it returns #N/A.
MATCH
Synopsis
MATCH(seek,vector,type)
Arguments
seek: value to find
vector: n by 1 or 1 by n range to be searched
type: +1 (the default) to find the largest value ≤ seek, 0 to find the first value = seek, or -1 to find the smallest value ≥ seek
Description
MATCH searches vector for seek and returns the 1-based index.
Note
For type = -1 the data must be sorted in descending order; for type = +1 the data must be sorted in ascending order. If seek could not be found, #N/A is returned. If vector is neither n by 1 nor 1 by n, #N/A is returned.
See also
OFFSET
Synopsis
OFFSET(range,row,col,height,width)
Arguments
range: reference or range
row: number of rows to offset range
col: number of columns to offset range
height: height of the offset range, defaults to height of range
width: width of the offset range, defaults to width of range
Description
OFFSET returns the cell range starting at offset (row,col) from range of height height and width width.
Note
If range is neither a reference nor a range, OFFSET returns #VALUE!
ROW
Synopsis
ROW(x)
Arguments
x: reference, defaults to the position of the current expression
Description
ROW function returns a 1xN array containing the sequence of integers from the first row to the last row of x.
Note
If x is neither an array nor a reference nor a range, returns #VALUE!
ROWS
Synopsis
ROWS(reference)
Arguments
reference: array, reference, or range
Note
If reference is neither an array nor a reference nor a range, ROWS returns #VALUE!
SHEET
Synopsis
SHEET(reference)
Arguments
reference: reference or literal sheet name, defaults to the current sheet
Note
If reference is neither a reference nor a literal sheet name, SHEET returns #VALUE!
See also
SHEETS
Synopsis
SHEETS(reference)
Arguments
reference: array, reference, or range, defaults to the maximum range
Note
If reference is neither an array nor a reference nor a range, SHEETS returns #VALUE!
SORT
Synopsis
SORT(ref,order)
Arguments
ref: list of numbers
order: 0 (descending order) or 1 (ascending order); defaults to 0
Note
Strings, booleans, and empty cells are ignored.
See also
VLOOKUP
Synopsis
VLOOKUP(value,range,column,approximate,as_index)
Arguments
value: search value
range: range to search
column: 1-based column offset indicating the return values
approximate: if false, an exact match of value must be found; defaults to TRUE
as_index: if true, the 0-based row offset is returned; defaults to FALSE
Description
VLOOKUP function finds the row in range that has a first cell similar to value. If approximate is not true it finds the row with an exact equality. If approximate is true, it finds the last row with first value less than or equal to value. If as_index is true the 0-based row offset is returned.
Note
If approximate is true, then the values must be sorted in order of ascending value. VLOOKUP returns #REF! if column falls outside range.
See also
A.12. Mathematics
- ABS — absolute value
- ACOS — the arc cosine of x
- ACOSH — the hyperbolic arc cosine of x
- ACOT — inverse cotangent of x
- ACOTH — the inverse hyperbolic cotangent of x
- AGM — the arithmetic-geometric mean
- ARABIC — the Roman numeral roman as number
- ASIN — the arc sine of x
- ASINH — the inverse hyperbolic sine of x
- ATAN — the arc tangent of x
- ATAN2 — the arc tangent of the ratio y/x
- ATANH — the inverse hyperbolic tangent of x
- AVERAGEIF — average of the cells in actual range for which the corresponding cells in the range meet the given criteria
- AVERAGEIFS — average of the cells in actual_range for which the corresponding cells in the range meet the given criteria
- BETA — Euler beta function
- BETALN — natural logarithm of the absolute value of the Euler beta function
- CEIL — smallest integer larger than or equal to x
- CEILING — nearest multiple of significance whose absolute value is at least ABS(x)
- CHOLESKY — the Cholesky decomposition of the symmetric positive-definite matrix
- COMBIN — binomial coefficient
- COMBINA — the number of k-combinations of an n-element set with repetition
- COS — the cosine of x
- COSH — the hyperbolic cosine of x
- COSPI — the cosine of Pi*x
- COT — the cotangent of x
- COTH — the hyperbolic cotangent of x
- COTPI — the cotangent of Pi*x
- COUNTIF — count of the cells meeting the given criteria
- COUNTIFS — count of the cells meeting the given criteria
- CSC — the cosecant of x
- CSCH — the hyperbolic cosecant of x
- DEGREES — equivalent degrees to x radians
- EIGEN — eigenvalues and eigenvectors of the symmetric matrix
- EVEN — x rounded away from 0 to the next even integer
- EXP — e raised to the power of x
- EXPM1 — EXP(x)-1
- FACT — the factorial of x, i.e. x!
- FACTDOUBLE — double factorial
- FIB — Fibonacci numbers
- FLOOR — nearest multiple of significance whose absolute value is at most ABS(x)
- G_PRODUCT — product of all the values and cells referenced
- GAMMA — the Gamma function
- GAMMALN — natural logarithm of the Gamma function
- GCD — the greatest common divisor
- GD — Gudermannian function
- HYPOT — the square root of the sum of the squares of the arguments
- IGAMMA — the incomplete Gamma function
- INT — largest integer not larger than x
- LAMBERTW — the Lambert W function
- LCM — the least common multiple
- LINSOLVE — solve linear equation
- LN — the natural logarithm of x
- LN1P — LN(1+x)
- LOG — logarithm of x with base base
- LOG10 — the base-10 logarithm of x
- LOG2 — the base-2 logarithm of x
- MAXIFS — maximum of the cells in actual_range for which the corresponding cells in the range meet the given criteria
- MDETERM — the determinant of the matrix matrix
- MINIFS — minimum of the cells in actual_range for which the corresponding cells in the range meet the given criteria
- MINVERSE — the inverse matrix of matrix
- MMULT — the matrix product of mat1 and mat2
- MOD — the remainder of x under division by n
- MPSEUDOINVERSE — the pseudo-inverse matrix of matrix
- MROUND — x rounded to a multiple of m
- MULTINOMIAL — multinomial coefficient (x1+⋯+xn) choose (x1,…,xn)
- MUNIT — the n by n identity matrix
- ODD — x rounded away from 0 to the next odd integer
- ODF.SUMPRODUCT — multiplies components and adds the results
- PI — the constant 𝜋
- POCHHAMMER — the value of GAMMA(x+n)/GAMMA(x)
- POWER — the value of x raised to the power y raised to the power of 1/z
- PRODUCT — product of the given values
- QUOTIENT — integer portion of a division
- RADIANS — the number of radians equivalent to x degrees
- REDUCEPI — reduce modulo Pi divided by a power of 2
- ROMAN — n as a roman numeral text
- ROUND — rounded x
- ROUNDDOWN — x rounded towards 0
- ROUNDUP — x rounded away from 0
- SEC — Secant
- SECH — the hyperbolic secant of x
- SERIESSUM — sum of a power series at x
- SIGN — sign of x
- SIN — the sine of x
- SINH — the hyperbolic sine of x
- SINPI — the sine of Pi*x
- SQRT — square root of x
- SQRTPI — the square root of x times 𝜋
- SUM — sum of the given values
- SUMA — sum of all values and cells referenced
- SUMIF — sum of the cells in actual_range for which the corresponding cells in the range meet the given criteria
- SUMIFS — sum of the cells in actual_range for which the corresponding cells in the range meet the given criteria
- SUMPRODUCT — multiplies components and adds the results
- SUMSQ — sum of the squares of all values and cells referenced
- SUMX2MY2 — sum of the difference of squares
- SUMX2PY2 — sum of the sum of squares
- SUMXMY2 — sum of the squares of differences
- TAN — the tangent of x
- TANH — the hyperbolic tangent of x
- TANPI — the tangent of Pi*x
- TRUNC — x truncated to d digits
ABS
Synopsis
ABS(x)
Arguments
x: number
Description
ABS gives the absolute value of x, i.e. the non-negative number of the same magnitude as x.
Microsoft Excel Compatibility
This function is Excel compatible.
ACOS
Synopsis
ACOS(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
ACOSH
Synopsis
ACOSH(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
AGM
Synopsis
AGM(a,b)
Arguments
a: value
b: value
Description
AGM computes the arithmetic-geometric mean of the two values.
ARABIC
Synopsis
ARABIC(roman)
Arguments
roman: Roman numeral
Description
Any Roman symbol to the left of a larger symbol (directly or indirectly) reduces the final value by the symbol amount, otherwise, it increases the final amount by the symbol's amount.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
ASIN
Synopsis
ASIN(x)
Arguments
x: number
Description
ASIN calculates the arc sine of x; that is the value whose sine is x.
Note
If x falls outside the range -1 to 1, ASIN returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
ASINH
Synopsis
ASINH(x)
Arguments
x: number
Description
ASINH calculates the inverse hyperbolic sine of x; that is the value whose hyperbolic sine is x.
Microsoft Excel Compatibility
This function is Excel compatible.
ATAN
Synopsis
ATAN(x)
Arguments
x: number
Description
ATAN calculates the arc tangent of x; that is the value whose tangent is x.
Note
The result will be between −π/2 and +π/2.
Microsoft Excel Compatibility
This function is Excel compatible.
ATAN2
Synopsis
ATAN2(x,y)
Arguments
x: x-coordinate
y: y-coordinate
Description
ATAN2 calculates the direction from the origin to the point (x,y) as an angle from the x-axis in radians.
Note
The result will be between −π and +π. The order of the arguments may be unexpected.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
ATANH
Synopsis
ATANH(x)
Arguments
x: number
Description
ATANH calculates the inverse hyperbolic tangent of x; that is the value whose hyperbolic tangent is x.
Note
If the absolute value of x is greater than 1.0, ATANH returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
AVERAGEIF
Synopsis
AVERAGEIF(range,criteria,actual_range)
Arguments
range: cell area
criteria: condition for a cell to be included
actual_range: cell area, defaults to range
Microsoft Excel Compatibility
This function is Excel compatible.
AVERAGEIFS
Synopsis
AVERAGEIFS(actual_range,range1,criteria1,…)
Arguments
actual_range: cell area
range1: cell area
criteria1: condition for a cell to be included
Microsoft Excel Compatibility
This function is Excel compatible.
BETA
Synopsis
BETA(x,y)
Arguments
x: number
y: number
Description
BETA function returns the value of the Euler beta function extended to all real numbers except 0 and negative integers.
Note
If x, y, or (x + y) are non-positive integers, BETA returns #NUM!
BETALN
Synopsis
BETALN(x,y)
Arguments
x: number
y: number
Description
BETALN function returns the natural logarithm of the absolute value of the Euler beta function extended to all real numbers except 0 and negative integers.
Note
If x, y, or (x + y) are non-positive integers, BETALN returns #NUM!
CEIL
Synopsis
CEIL(x)
Arguments
x: number
Description
CEIL(x) is the smallest integer that is at least as large as x.
OpenDocument Format (ODF) Compatibility
This function is the OpenFormula function CEILING(x).
CEILING
Synopsis
CEILING(x,significance)
Arguments
x: number
significance: base multiple (defaults to 1 for x > 0 and -1 for x < 0)
Description
CEILING(x,significance) is the nearest multiple of significance whose absolute value is at least ABS(x).
Note
If x or significance is non-numeric, CEILING returns a #VALUE! error. If x and significance have different signs, CEILING returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
CEILING(x) is exported to ODF as CEILING(x,SIGN(x),1). CEILING(x,significance) is the OpenFormula function CEILING(x,significance,1).
CHOLESKY
Synopsis
CHOLESKY(matrix)
Arguments
matrix: a symmetric positive definite matrix
Note
If the Cholesky-Banachiewicz algorithm applied to matrix fails, Cholesky returns #NUM! If matrix does not contain an equal number of columns and rows, CHOLESKY returns #VALUE!
COMBIN
Synopsis
COMBIN(n,k)
Arguments
n: non-negative integer
k: non-negative integer
Description
COMBIN returns the binomial coefficient "n choose k", the number of k-combinations of an n-element set without repetition.
Note
If n is less than k COMBIN returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
COMBINA
Synopsis
COMBINA(n,k)
Arguments
n: non-negative integer
k: non-negative integer
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
COS
Synopsis
COS(x)
Arguments
x: angle in radians
Description
This function is Excel compatible.
COSH
Synopsis
COSH(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
COTPI
Synopsis
COTPI(x)
Arguments
x: number of half turns
See also
COT.
COUNTIF
Synopsis
COUNTIF(range,criteria)
Arguments
range: cell area
criteria: condition for a cell to be counted
Microsoft Excel Compatibility
This function is Excel compatible.
COUNTIFS
Synopsis
COUNTIFS(range,criteria,…)
Arguments
range: cell area
criteria: condition for a cell to be counted
Microsoft Excel Compatibility
This function is Excel compatible.
CSC
Synopsis
CSC(x)
Arguments
x: angle in radians
Microsoft Excel Compatibility
This function is not Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
CSCH
Synopsis
CSCH(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is not Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
DEGREES
Synopsis
DEGREES(x)
Arguments
x: angle in radians
Microsoft Excel Compatibility
This function is Excel compatible.
EIGEN
Synopsis
EIGEN(matrix)
Arguments
matrix: a symmetric matrix
Note
If matrix is not symmetric, matching off-diagonal cells will be averaged on the assumption that the non-symmetry is caused by unimportant rounding errors. If matrix does not contain an equal number of columns and rows, EIGEN returns #VALUE!
EVEN
Synopsis
EVEN(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ODD.
EXP
Synopsis
EXP(x)
Arguments
x: number
Note
e is the base of the natural logarithm.
Microsoft Excel Compatibility
This function is Excel compatible.
EXPM1
Synopsis
EXPM1(x)
Arguments
x: number
Note
This function has a higher resulting precision than evaluating EXP(x)-1.
FACT
Synopsis
FACT(x)
Arguments
x: number
Note
The domain of this function has been extended using the GAMMA function.
Microsoft Excel Compatibility
This function is Excel compatible.
FACTDOUBLE
Synopsis
FACTDOUBLE(x)
Arguments
x: non-negative integer
Description
FACTDOUBLE function returns the double factorial x!!
Note
If x is not an integer, it is truncated. If x is negative, FACTDOUBLE returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
See also
FACT.
FIB
Synopsis
FIB(n)
Arguments
n: positive integer
Description
FIB(n) is the nth Fibonacci number.
Note
If n is not an integer, it is truncated. If it is negative or zero FIB returns #NUM!
FLOOR
Synopsis
FLOOR(x,significance)
Arguments
x: number
significance: base multiple (defaults to 1 for x > 0 and -1 for x < 0)
Description
FLOOR(x,significance) is the nearest multiple of significance whose absolute value is at most ABS(x)
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
FLOOR(x) is exported to ODF as FLOOR(x,SIGN(x),1). FLOOR(x,significance) is the OpenFormula function FLOOR(x,significance,1).
G_PRODUCT
Synopsis
G_PRODUCT(x1,x2,…)
Arguments
x1: number
x2: number
Note
Empty cells are ignored and the empty product is 1.
GAMMALN
Synopsis
GAMMALN(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
See also
GCD
Synopsis
GCD(n0,n1,…)
Arguments
n0: positive integer
n1: positive integer
Description
GCD calculates the greatest common divisor of the given numbers n0,n1,..., the greatest integer that is a divisor of each argument.
Note
If any of the arguments is not an integer, it is truncated.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
LCM.
HYPOT
Synopsis
HYPOT(n0,n1,…)
Arguments
n0: number
n1: number
IGAMMA
Synopsis
IGAMMA(a,x,lower,regularize,real)
Arguments
a: number
x: number
lower: if true (the default), the lower incomplete gamma function, otherwise the upper incomplete gamma function
regularize: if true (the default), the regularized version of the incomplete gamma function
real: if true (the default), the real part of the result, otherwise the imaginary part
Note
The regularized incomplete gamma function is the unregularized incomplete gamma function divided by GAMMA(a) This is a real valued function as long as neither a nor z are negative.
INT
Synopsis
INT(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
LAMBERTW
Synopsis
LAMBERTW(x,k)
Arguments
x: number
k: branch
Note
k defaults to 0, the principal branch. k must be either 0 or -1.
See also
EXP.
LCM
Synopsis
LCM(n0,n1,…)
Arguments
n0: positive integer
n1: positive integer
Description
LCM calculates the least common multiple of the given numbers n0,n1,..., the smallest integer that is a multiple of each argument.
Note
If any of the arguments is not an integer, it is truncated.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
GCD.
LINSOLVE
Synopsis
LINSOLVE(A,B)
Arguments
A: a matrix
B: a matrix
Description
Solves the equation A*X=B and returns X.
Note
If the matrix A is singular, #VALUE! is returned.
See also
LN
Synopsis
LN(x)
Arguments
x: positive number
Note
If x ≤ 0, LN returns #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
LN1P
Synopsis
LN1P(x)
Arguments
x: positive number
Description
LN1P calculates LN(1+x) but yielding a higher precision than evaluating LN(1+x).
Note
If x ≤ -1, LN returns #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
LOG
Synopsis
LOG(x,base)
Arguments
x: positive number
base: base of the logarithm, defaults to 10
Note
base must be positive and not equal to 1. If x ≤ 0, LOG returns #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
LOG10
Synopsis
LOG10(x)
Arguments
x: positive number
Note
If x ≤ 0, LOG10 returns #NUM!
LOG2
Synopsis
LOG2(x)
Arguments
x: positive number
Note
If x ≤ 0, LOG2 returns #NUM!
MAXIFS
Synopsis
MAXIFS(actual_range,range1,criteria1,…)
Arguments
actual_range: cell area
range1: cell area
criteria1: condition for a cell to be included
Microsoft Excel Compatibility
This function is Excel compatible.
MDETERM
Synopsis
MDETERM(matrix)
Arguments
matrix: a square matrix
Microsoft Excel Compatibility
This function is Excel compatible.
MINIFS
Synopsis
MINIFS(actual_range,range1,criteria1,…)
Arguments
actual_range: cell area
range1: cell area
criteria1: condition for a cell to be included
Microsoft Excel Compatibility
This function is Excel compatible.
MINVERSE
Synopsis
MINVERSE(matrix)
Arguments
matrix: a square matrix
Note
If matrix is not invertible, MINVERSE returns #NUM! If matrix does not contain an equal number of columns and rows, MINVERSE returns #VALUE!
Microsoft Excel Compatibility
This function is Excel compatible.
MMULT
Synopsis
MMULT(mat1,mat2)
Arguments
mat1: a matrix
mat2: a matrix
Note
The number of columns in mat1 must equal the number of rows in mat2; otherwise #VALUE! is returned. The result of MMULT is an array, in which the number of rows is the same as in mat1), and the number of columns is the same as in (mat2).
Microsoft Excel Compatibility
This function is Excel compatible.
MOD
Synopsis
MOD(x,n)
Arguments
x: integer
n: integer
Description
MOD function returns the remainder when x is divided by n.
Note
If n is 0, MOD returns #DIV/0!
Microsoft Excel Compatibility
This function is Excel compatible.
MPSEUDOINVERSE
Synopsis
MPSEUDOINVERSE(matrix,threshold)
Arguments
matrix: a matrix
threshold: a relative size threshold for discarding eigenvalues
See also
MROUND
Synopsis
MROUND(x,m)
Arguments
x: number
m: number
Note
If x and m have different sign, MROUND returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
MULTINOMIAL
Synopsis
MULTINOMIAL(x1,x2,xn,…)
Arguments
x1: first number
x2: second number
xn: nth number
Microsoft Excel Compatibility
This function is Excel compatible.
MUNIT
Synopsis
MUNIT(n)
Arguments
n: size of the matrix
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
ODD
Synopsis
ODD(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
See also
EVEN.
ODF.SUMPRODUCT
Synopsis
ODF.SUMPRODUCT(,…)Description
Multiplies corresponding data entries in the given arrays or ranges, and then returns the sum of those products.
Note
If an entry is not numeric or logical, the value zero is used instead. If arrays or range arguments do not have the same dimensions, return #VALUE! error. This function differs from SUMPRODUCT by considering booleans.
Microsoft Excel Compatibility
This function is not Excel compatible. Use SUMPRODUCT instead.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
PI
Synopsis
PI()Microsoft Excel Compatibility
This function is Excel compatible, but it returns 𝜋 with a better precision.
See also
POCHHAMMER
Synopsis
POCHHAMMER(x,n)
Arguments
x: number
n: number
See also
POWER
Synopsis
POWER(x,y,z)
Arguments
x: number
y: number
z: number
Note
If both x and y equal 0, POWER returns #NUM! If x = 0 and y < 0, POWER returns #DIV/0! If x < 0 and y is not an integer, POWER returns #NUM! z defaults to 1 If z is not a positive integer, POWER returns #NUM! If x < 0, y is odd, and z is even, POWER returns #NUM!
See also
EXP.
PRODUCT
Synopsis
PRODUCT(values,…)
Arguments
values: a list of values to multiply
Description
PRODUCT computes the product of all the values and cells referenced in the argument list.
Note
If all cells are empty, the result will be 0.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
QUOTIENT
Synopsis
QUOTIENT(numerator,denominator)
Arguments
numerator: integer
denominator: non-zero integer
Description
QUOTIENT yields the integer portion of the division numerator/denominator.
QUOTIENT (numerator,denominator)⨉denominator+MOD(numerator,denominator)=numerator
Microsoft Excel Compatibility
This function is Excel compatible.
See also
MOD.
RADIANS
Synopsis
RADIANS(x)
Arguments
x: angle in degrees
Microsoft Excel Compatibility
This function is Excel compatible.
REDUCEPI
Synopsis
REDUCEPI(x,e,q)
Arguments
x: number
e: scale
q: get lower bits of quotient, defaults to FALSE
Note
This function returns a value, xr, such that x=xr+j*Pi/2^e where j is an integer and the absolute value of xr does not exceed Pi/2^(e+1). If optional argument q is TRUE, returns instead the e+1 lower bits of j. The reduction is performed as-if using an exact value of Pi. The lowest valid e is -1 representing reduction modulo 2*Pi; the highest is 7 representing reduction modulo Pi/256.
See also
PI.
ROMAN
Synopsis
ROMAN(n,type)
Arguments
n: non-negative integer
type: 0,1,2,3,or 4, defaults to 0
Description
ROMAN returns the arabic number n as a roman numeral text.
If type is 0 or it is omitted, ROMAN returns classic roman numbers.
Type 1 is more concise than classic type, type 2 is more concise than type 1, and type 3 is more concise than type 2. Type 4 is a simplified type.
Microsoft Excel Compatibility
This function is Excel compatible.
ROUND
Synopsis
ROUND(x,d)
Arguments
x: number
d: integer, defaults to 0
Description
If d is greater than zero, x is rounded to the given number of digits.
If d is zero, x is rounded to the next integer.
If d is less than zero, x is rounded to the left of the decimal point
Microsoft Excel Compatibility
This function is Excel compatible.
ROUNDDOWN
Synopsis
ROUNDDOWN(x,d)
Arguments
x: number
d: integer, defaults to 0
Description
If d is greater than zero, x is rounded toward 0 to the given number of digits.
If d is zero, x is rounded toward 0 to the next integer.
If d is less than zero, x is rounded toward 0 to the left of the decimal point
Microsoft Excel Compatibility
This function is Excel compatible.
ROUNDUP
Synopsis
ROUNDUP(x,d)
Arguments
x: number
d: integer, defaults to 0
Description
If d is greater than zero, x is rounded away from 0 to the given number of digits.
If d is zero, x is rounded away from 0 to the next integer.
If d is less than zero, x is rounded away from 0 to the left of the decimal point
Microsoft Excel Compatibility
This function is Excel compatible.
SEC
Synopsis
SEC(x)
Arguments
x: angle in radians
Microsoft Excel Compatibility
This function is not Excel compatible.
OpenDocument Format (ODF) Compatibility
SEC(x) is exported to OpenFormula as 1/COS(x).
SECH
Synopsis
SECH(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is not Excel compatible.
OpenDocument Format (ODF) Compatibility
SECH(x) is exported to OpenFormula as 1/COSH(x).
SERIESSUM
Synopsis
SERIESSUM(x,n,m,coeff)
Arguments
x: number where to evaluate the power series
n: non-negative integer, exponent of the lowest term of the series
m: increment to each exponent
coeff: coefficients of the power series
Microsoft Excel Compatibility
This function is Excel compatible.
SIGN
Synopsis
SIGN(x)
Arguments
x: number
Description
SIGN returns 1 if the x is positive and it returns -1 if x is negative.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ABS.
SIN
Synopsis
SIN(x)
Arguments
x: angle in radians
Microsoft Excel Compatibility
This function is Excel compatible.
SINH
Synopsis
SINH(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
SQRT
Synopsis
SQRT(x)
Arguments
x: non-negative number
Note
If x is negative, SQRT returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
See also
SQRTPI
Synopsis
SQRTPI(x)
Arguments
x: non-negative number
Microsoft Excel Compatibility
This function is Excel compatible.
See also
PI.
SUM
Synopsis
SUM(values,…)
Arguments
values: a list of values to add
Description
SUM computes the sum of all the values and cells referenced in the argument list.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
SUMA
Synopsis
SUMA(area0,area1,…)
Arguments
area0: first cell area
area1: second cell area
Description
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1).
SUMIF
Synopsis
SUMIF(range,criteria,actual_range)
Arguments
range: cell area
criteria: condition for a cell to be summed
actual_range: cell area, defaults to range
Note
If the actual_range has a size that differs from the size of range, actual_range is resized (retaining the top-left corner) to match the size of range.
Microsoft Excel Compatibility
This function is Excel compatible.
SUMIFS
Synopsis
SUMIFS(actual_range,range1,criteria1,…)
Arguments
actual_range: cell area
range1: cell area
criteria1: condition for a cell to be included
Microsoft Excel Compatibility
This function is Excel compatible.
SUMPRODUCT
Synopsis
SUMPRODUCT(,…)Description
Multiplies corresponding data entries in the given arrays or ranges, and then returns the sum of those products.
Note
If an entry is not numeric, the value zero is used instead. If arrays or range arguments do not have the same dimensions, return #VALUE! error. This function ignores logicals, so using SUMPRODUCT(A1:A5>0) will not work. Instead use SUMPRODUCT(--(A1:A5>0))
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is not OpenFormula compatible. Use ODF.SUMPRODUCT instead.
See also
SUMSQ
Synopsis
SUMSQ(area0,area1,…)
Arguments
area0: first cell area
area1: second cell area
Microsoft Excel Compatibility
This function is Excel compatible.
SUMX2MY2
Synopsis
SUMX2MY2(array0,array1)
Arguments
array0: first cell area
array1: second cell area
Description
SUMX2MY2 function returns the sum of the difference of squares of corresponding values in two arrays. The equation of SUMX2MY2 is SUM(x^2-y^2).
Microsoft Excel Compatibility
This function is Excel compatible.
SUMX2PY2
Synopsis
SUMX2PY2(array0,array1)
Arguments
array0: first cell area
array1: second cell area
Description
SUMX2PY2 function returns the sum of the sum of squares of corresponding values in two arrays. The equation of SUMX2PY2 is SUM(x^2+y^2).
Note
If array0 and array1 have different number of data points, SUMX2PY2 returns #N/A.
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
SUMXMY2
Synopsis
SUMXMY2(array0,array1)
Arguments
array0: first cell area
array1: second cell area
Description
SUMXMY2 function returns the sum of the squares of the differences of corresponding values in two arrays. The equation of SUMXMY2 is SUM((x-y)^2).
Note
If array0 and array1 have different number of data points, SUMXMY2 returns #N/A.
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
TAN
Synopsis
TAN(x)
Arguments
x: angle in radians
Microsoft Excel Compatibility
This function is Excel compatible.
TANH
Synopsis
TANH(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
TRUNC
Synopsis
TRUNC(x,d)
Arguments
x: number
d: non-negative integer, defaults to 0
Note
If d is omitted or negative then it defaults to zero. If it is not an integer then it is truncated to an integer.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
INT.
A.13. Number Theory
- ISPRIME — whether n is prime
- ITHPRIME — ith prime
- NT_D — number of divisors
- NT_MU — Möbius mu function
- NT_OMEGA — Number of distinct prime factors
- NT_PHI — Euler's totient function
- NT_PI — number of primes upto n
- NT_RADICAL — Radical function
- NT_SIGMA — sigma function
- PFACTOR — smallest prime factor
ISPRIME
Synopsis
ISPRIME(n)
Arguments
n: positive integer
Description
ISPRIME returns TRUE if n is prime and FALSE otherwise.
ITHPRIME
Synopsis
ITHPRIME(i)
Arguments
i: positive integer
Description
ITHPRIME finds the ith prime.
NT_D
Synopsis
NT_D(n)
Arguments
n: positive integer
Description
NT_D calculates the number of divisors of n.
NT_MU
Synopsis
NT_MU(n)
Arguments
n: positive integer
Description
NT_MU function (Möbius mu function) returns 0 if n is divisible by the square of a prime. Otherwise, if n has an odd number of different prime factors, NT_MU returns -1, and if n has an even number of different prime factors, it returns 1. If n = 1, NT_MU returns 1.
NT_OMEGA
Synopsis
NT_OMEGA(n)
Arguments
n: positive integer
Note
Returns the number of distinct prime factors without multiplicity.
NT_PHI
Synopsis
NT_PHI(n)
Arguments
n: positive integer
Note
Euler's totient function gives the number of integers less than or equal to n that are relatively prime (coprime) to n.
NT_PI
Synopsis
NT_PI(n)
Arguments
n: positive integer
Description
NT_PI returns the number of primes less than or equal to n.
NT_RADICAL
Synopsis
NT_RADICAL(n)
Arguments
n: positive integer
Note
The function computes the product of its distinct prime factors
NT_SIGMA
Synopsis
NT_SIGMA(n)
Arguments
n: positive integer
Description
NT_SIGMA calculates the sum of the divisors of n.
A.14. Random Numbers
- RAND — a random number between zero and one
- RANDBERNOULLI — random variate from a Bernoulli distribution
- RANDBETA — random variate from a Beta distribution
- RANDBETWEEN — a random integer number between and including bottom and top
- RANDBINOM — random variate from a binomial distribution
- RANDCAUCHY — random variate from a Cauchy or Lorentz distribution
- RANDCHISQ — random variate from a Chi-square distribution
- RANDDISCRETE — random variate from a finite discrete distribution
- RANDEXP — random variate from an exponential distribution
- RANDEXPPOW — random variate from an exponential power distribution
- RANDFDIST — random variate from an F distribution
- RANDGAMMA — random variate from a Gamma distribution
- RANDGEOM — random variate from a geometric distribution
- RANDGUMBEL — random variate from a Gumbel distribution
- RANDHYPERG — random variate from a hypergeometric distribution
- RANDLANDAU — random variate from the Landau distribution
- RANDLAPLACE — random variate from a Laplace distribution
- RANDLEVY — random variate from a Lévy distribution
- RANDLOG — random variate from a logarithmic distribution
- RANDLOGISTIC — random variate from a logistic distribution
- RANDLOGNORM — random variate from a lognormal distribution
- RANDNEGBINOM — random variate from a negative binomial distribution
- RANDNORM — random variate from a normal distribution
- RANDNORMTAIL — random variate from the upper tail of a normal distribution with mean 0
- RANDPARETO — random variate from a Pareto distribution
- RANDPOISSON — random variate from a Poisson distribution
- RANDRAYLEIGH — random variate from a Rayleigh distribution
- RANDRAYLEIGHTAIL — random variate from the tail of a Rayleigh distribution
- RANDSNORM — random variate from a skew-normal distribution
- RANDSTDIST — random variate from a skew-t distribution
- RANDTDIST — random variate from a Student t distribution
- RANDUNIFORM — random variate from the uniform distribution from a to b
- RANDWEIBULL — random variate from a Weibull distribution
- SIMTABLE — one of the values in the given argument list depending on the round number of the simulation tool
RAND
Synopsis
RAND()Microsoft Excel Compatibility
This function is Excel compatible.
See also
RANDBERNOULLI
Synopsis
RANDBERNOULLI(p)
Arguments
p: probability of success
Note
If p < 0 or p > 1 RANDBERNOULLI returns #NUM!
See also
RANDBETA
Synopsis
RANDBETA(a,b)
Arguments
a: parameter of the Beta distribution
b: parameter of the Beta distribution
RANDBETWEEN
Synopsis
RANDBETWEEN(bottom,top)
Arguments
bottom: lower limit
top: upper limit
Note
If bottom > top, RANDBETWEEN returns #NUM!
Microsoft Excel Compatibility
This function is Excel compatible.
See also
RANDBINOM
Synopsis
RANDBINOM(p,n)
Arguments
p: probability of success in a single trial
n: number of trials
Note
If p < 0 or p > 1 RANDBINOM returns #NUM! If n < 0 RANDBINOM returns #NUM!
See also
RANDCAUCHY
Synopsis
RANDCAUCHY(a)
Arguments
a: scale parameter of the distribution
Note
If a < 0 RANDCAUCHY returns #NUM!
See also
RAND.
RANDCHISQ
Synopsis
RANDCHISQ(df)
Arguments
df: degrees of freedom
RANDDISCRETE
Synopsis
RANDDISCRETE(val_range,prob_range)
Arguments
val_range: possible values of the random variable
prob_range: probabilities of the corresponding values in val_range, defaults to equal probabilities
Description
RANDDISCRETE returns one of the values in the val_range. The probabilities for each value are given in the prob_range.
Note
If the sum of all values in prob_range is not one, RANDDISCRETE returns #NUM! If val_range and prob_range are not the same size, RANDDISCRETE returns #NUM! If val_range or prob_range is not a range, RANDDISCRETE returns #VALUE!
See also
RANDEXP
Synopsis
RANDEXP(b)
Arguments
b: parameter of the exponential distribution
See also
RANDEXPPOW
Synopsis
RANDEXPPOW(a,b)
Arguments
a: scale parameter of the exponential power distribution
b: exponent of the exponential power distribution
Description
For b = 1 the exponential power distribution reduces to the Laplace distribution.
For b = 2 the exponential power distribution reduces to the normal distribution with σ = a/sqrt(2)
See also
RAND.
RANDFDIST
Synopsis
RANDFDIST(df1,df2)
Arguments
df1: numerator degrees of freedom
df2: denominator degrees of freedom
RANDGAMMA
Synopsis
RANDGAMMA(a,b)
Arguments
a: shape parameter of the Gamma distribution
b: scale parameter of the Gamma distribution
Note
If a ≤ 0, RANDGAMMA returns #NUM!
See also
RAND.
RANDGEOM
Synopsis
RANDGEOM(p)
Arguments
p: probability of success in a single trial
Note
If p < 0 or p > 1 RANDGEOM returns #NUM!
See also
RAND.
RANDGUMBEL
Synopsis
RANDGUMBEL(a,b,type)
Arguments
a: parameter of the Gumbel distribution
b: parameter of the Gumbel distribution
type: type of the Gumbel distribution, defaults to 1
Note
If type is neither 1 nor 2, RANDGUMBEL returns #NUM!
See also
RAND.
RANDHYPERG
Synopsis
RANDHYPERG(n1,n2,t)
Arguments
n1: number of objects of type 1
n2: number of objects of type 2
t: total number of objects selected
See also
RAND.
RANDLANDAU
Synopsis
RANDLANDAU()See also
RAND.
RANDLAPLACE
Synopsis
RANDLAPLACE(a)
Arguments
a: parameter of the Laplace distribution
See also
RAND.
RANDLEVY
Synopsis
RANDLEVY(c,α,β)
Arguments
c: parameter of the Lévy distribution
α: parameter of the Lévy distribution
β: parameter of the Lévy distribution, defaults to 0
Description
For α = 1, β=0, the Lévy distribution reduces to the Cauchy (or Lorentzian) distribution.
For α = 2, β=0, the Lévy distribution reduces to the normal distribution.
Note
If α ≤ 0 or α > 2, RANDLEVY returns #NUM! If β < -1 or β > 1, RANDLEVY returns #NUM!
See also
RAND.
RANDLOG
Synopsis
RANDLOG(p)
Arguments
p: probability
Note
If p < 0 or p > 1 RANDLOG returns #NUM!
See also
RAND.
RANDLOGISTIC
Synopsis
RANDLOGISTIC(a)
Arguments
a: parameter of the logistic distribution
See also
RAND.
RANDLOGNORM
Synopsis
RANDLOGNORM(ζ,σ)
Arguments
ζ: parameter of the lognormal distribution
σ: standard deviation of the distribution
Note
If σ < 0, RANDLOGNORM returns #NUM!
See also
RAND.
RANDNEGBINOM
Synopsis
RANDNEGBINOM(p,n)
Arguments
p: probability of success in a single trial
n: number of failures
Note
If p < 0 or p > 1 RANDNEGBINOM returns #NUM! If n < 1 RANDNEGBINOM returns #NUM!
See also
RANDNORM
Synopsis
RANDNORM(μ,σ)
Arguments
μ: mean of the distribution
σ: standard deviation of the distribution
Note
If σ < 0, RANDNORM returns #NUM!
See also
RAND.
RANDNORMTAIL
Synopsis
RANDNORMTAIL(a,σ)
Arguments
a: lower limit of the tail
σ: standard deviation of the normal distribution
Note
The method is based on Marsaglia's famous rectangle-wedge-tail algorithm (Ann Math Stat 32, 894-899 (1961)), with this aspect explained in Knuth, v2, 3rd ed, p139, 586 (exercise 11).
See also
RAND.
RANDPARETO
Synopsis
RANDPARETO(a,b)
Arguments
a: parameter of the Pareto distribution
b: parameter of the Pareto distribution
See also
RAND.
RANDPOISSON
Synopsis
RANDPOISSON(λ)
Arguments
λ: parameter of the Poisson distribution
Note
If λ < 0 RANDPOISSON returns #NUM!
See also
RANDRAYLEIGH
Synopsis
RANDRAYLEIGH(σ)
Arguments
σ: scale parameter of the Rayleigh distribution
See also
RAND.
RANDRAYLEIGHTAIL
Synopsis
RANDRAYLEIGHTAIL(a,σ)
Arguments
a: lower limit of the tail
σ: scale parameter of the Rayleigh distribution
See also
RANDSNORM
Synopsis
RANDSNORM(𝛼,𝜉,𝜔)
Arguments
𝛼: shape parameter of the skew-normal distribution, defaults to 0
𝜉: location parameter of the skew-normal distribution, defaults to 0
𝜔: scale parameter of the skew-normal distribution, defaults to 1
Description
The random variates are drawn from a skew-normal distribution with shape parameter 𝛼. When 𝛼=0, the skewness vanishes, and we obtain the standard normal density; as 𝛼 increases (in absolute value), the skewness of the distribution increases; when 𝛼 approaches infinity the density converges to the so-called half-normal (or folded normal) density function; if the sign of 𝛼 changes, the density is reflected on the opposite side of the vertical axis.
Note
The mean of a skew-normal distribution with location parameter 𝜉=0 is not 0. The standard deviation of a skew-normal distribution with scale parameter 𝜔=1 is not 1. The skewness of a skew-normal distribution is in general not 𝛼. If 𝜔 < 0, RANDSNORM returns #NUM!
See also
RANDSTDIST
Synopsis
RANDSTDIST(df,𝛼)
Arguments
df: degrees of freedom
𝛼: shape parameter of the skew-t distribution, defaults to 0
Note
The mean of a skew-t distribution is not 0. The standard deviation of a skew-t distribution is not 1. The skewness of a skew-t distribution is in general not 𝛼.
RANDTDIST
Synopsis
RANDTDIST(df)
Arguments
df: degrees of freedom
See also
RAND.
RANDUNIFORM
Synopsis
RANDUNIFORM(a,b)
Arguments
a: lower limit of the uniform distribution
b: upper limit of the uniform distribution
Note
If a > b RANDUNIFORM returns #NUM!
See also
RANDWEIBULL
Synopsis
RANDWEIBULL(a,b)
Arguments
a: scale parameter of the Weibull distribution
b: shape parameter of the Weibull distribution
See also
RAND.
SIMTABLE
Synopsis
SIMTABLE(d1,d2,…)
Arguments
d1: first value
d2: second value
Description
SIMTABLE returns one of the values in the given argument list depending on the round number of the simulation tool. When the simulation tool is not activated, SIMTABLE returns d1.
With the simulation tool and the SIMTABLE function you can test given decision variables. Each SIMTABLE function contains the possible values of a simulation variable. In most valid simulation models you should have the same number of values dN for all decision variables. If the simulation is run more rounds than there are values defined, SIMTABLE returns #N/A error (e.g. if A1 contains `=SIMTABLE(1)' and A2 `=SIMTABLE(1,2)', A1 yields #N/A error on the second round).
The successive use of the simulation tool also requires that you give to the tool at least one input variable having RAND() or any other RAND<distribution name>() function in it. On each round, the simulation tool iterates for the given number of rounds over all the input variables to reevaluate them. On each iteration, the values of the output variables are stored, and when the round is completed, descriptive statistical information is created according to the values.
A.15. Statistics
- ADTEST — Anderson-Darling Test of Normality
- AVEDEV — average of the absolute deviations of a data set
- AVERAGE — average of all the numeric values and cells
- AVERAGEA — average of all the values and cells
- BERNOULLI — probability mass function of a Bernoulli distribution
- BETA.DIST — cumulative distribution function of the beta distribution
- BETADIST — cumulative distribution function of the beta distribution
- BETAINV — inverse of the cumulative distribution function of the beta distribution
- BINOM.DIST.RANGE — probability of the binomial distribution over an interval
- BINOMDIST — probability mass or cumulative distribution function of the binomial distribution
- CAUCHY — probability density or cumulative distribution function of the Cauchy, Lorentz or Breit-Wigner distribution
- CHIDIST — survival function of the chi-squared distribution
- CHIINV — inverse of the survival function of the chi-squared distribution
- CHITEST — p value of the Goodness of Fit Test
- CONFIDENCE — margin of error of a confidence interval for the population mean
- CONFIDENCE.T — margin of error of a confidence interval for the population mean using the Student's t-distribution
- CORREL — Pearson correlation coefficient of two data sets
- COUNT — total number of integer or floating point arguments passed
- COUNTA — number of arguments passed not including empty cells
- COVAR — covariance of two data sets
- COVARIANCE.S — sample covariance of two data sets
- CRITBINOM — right-tailed critical value of the binomial distribution
- CRONBACH — Cronbach's alpha
- CVMTEST — Cramér-von Mises Test of Normality
- DEVSQ — sum of squares of deviations of a data set
- EXPONDIST — probability density or cumulative distribution function of the exponential distribution
- EXPPOWDIST — the probability density function of the Exponential Power distribution
- FDIST — survival function of the F distribution
- FINV — inverse of the survival function of the F distribution
- FISHER — Fisher transformation
- FISHERINV — inverse of the Fisher transformation
- FORECAST — estimates a future value according to existing values using simple linear regression
- FREQUENCY — frequency table
- FTEST — p-value for the two-tailed hypothesis test comparing the variances of two populations
- GAMMADIST — probability density or cumulative distribution function of the gamma distribution
- GAMMAINV — inverse of the cumulative gamma distribution
- GEOMDIST — probability mass or cumulative distribution function of the geometric distribution
- GEOMEAN — geometric mean
- GROWTH — exponential growth prediction
- HARMEAN — harmonic mean
- HYPGEOMDIST — probability mass or cumulative distribution function of the hypergeometric distribution
- INTERCEPT — the intercept of a linear regression line
- KURT — unbiased estimate of the kurtosis of a data set
- KURTP — population kurtosis of a data set
- LANDAU — approximate probability density function of the Landau distribution
- LAPLACE — probability density function of the Laplace distribution
- LARGE — k-th largest value in a data set
- LEVERAGE — calculate regression leverage
- LINEST — multiple linear regression coefficients and statistics
- LKSTEST — Lilliefors (Kolmogorov-Smirnov) Test of Normality
- LOGEST — exponential least square fit
- LOGFIT — logarithmic least square fit (using a trial and error method)
- LOGINV — inverse of the cumulative distribution function of the lognormal distribution
- LOGISTIC — probability density function of the logistic distribution
- LOGNORMDIST — cumulative distribution function of the lognormal distribution
- LOGREG — the logarithmic regression
- MAX — largest value, with negative numbers considered smaller than positive numbers
- MAXA — largest value, with negative numbers considered smaller than positive numbers
- MEDIAN — median of a data set
- MIN — smallest value, with negative numbers considered smaller than positive numbers
- MINA — smallest value, with negative numbers considered smaller than positive numbers
- MODE — first most common number in the dataset
- MODE.MULT — most common numbers in the dataset
- NEGBINOMDIST — probability mass function of the negative binomial distribution
- NORMDIST — probability density or cumulative distribution function of a normal distribution
- NORMINV — inverse of the cumulative distribution function of a normal distribution
- NORMSDIST — cumulative distribution function of the standard normal distribution
- NORMSINV — inverse of the cumulative distribution function of the standard normal distribution
- OWENT — Owen's T function
- PARETO — probability density function of the Pareto distribution
- PEARSON — Pearson correlation coefficient of the paired set of data
- PERCENTILE — determines the 100*k-th percentile of the given data points (Hyndman-Fan method 7: N-1 basis)
- PERCENTILE.EXC — determines the 100*k-th percentile of the given data points (Hyndman-Fan method 6: N+1 basis)
- PERCENTRANK — rank of a data point in a data set (Hyndman-Fan method 7: N-1 basis)
- PERCENTRANK.EXC — rank of a data point in a data set (Hyndman-Fan method 6: N+1 basis)
- PERMUT — number of k-permutations of a n-set
- PERMUTATIONA — the number of permutations of y objects chosen from x objects with repetition allowed
- POISSON — probability mass or cumulative distribution function of the Poisson distribution
- PROB — probability of an interval for a discrete (and finite) probability distribution
- QUARTILE — the k-th quartile of the data points (Hyndman-Fan method 7: N-1 basis)
- QUARTILE.EXC — the k-th quartile of the data points (Hyndman-Fan method 6: N+1 basis)
- R.DBETA — probability density function of the beta distribution
- R.DBINOM — probability density function of the binomial distribution
- R.DCAUCHY — probability density function of the Cauchy distribution
- R.DCHISQ — probability density function of the chi-square distribution
- R.DEXP — probability density function of the exponential distribution
- R.DF — probability density function of the F distribution
- R.DGAMMA — probability density function of the gamma distribution
- R.DGEOM — probability density function of the geometric distribution
- R.DGUMBEL — probability density function of the Gumbel distribution
- R.DHYPER — probability density function of the hypergeometric distribution
- R.DLNORM — probability density function of the log-normal distribution
- R.DNBINOM — probability density function of the negative binomial distribution
- R.DNORM — probability density function of the normal distribution
- R.DPOIS — probability density function of the Poisson distribution
- R.DRAYLEIGH — probability density function of the Rayleigh distribution
- R.DSNORM — probability density function of the skew-normal distribution
- R.DST — probability density function of the skew-t distribution
- R.DT — probability density function of the Student t distribution
- R.DWEIBULL — probability density function of the Weibull distribution
- R.PBETA — cumulative distribution function of the beta distribution
- R.PBINOM — cumulative distribution function of the binomial distribution
- R.PCAUCHY — cumulative distribution function of the Cauchy distribution
- R.PCHISQ — cumulative distribution function of the chi-square distribution
- R.PEXP — cumulative distribution function of the exponential distribution
- R.PF — cumulative distribution function of the F distribution
- R.PGAMMA — cumulative distribution function of the gamma distribution
- R.PGEOM — cumulative distribution function of the geometric distribution
- R.PGUMBEL — cumulative distribution function of the Gumbel distribution
- R.PHYPER — cumulative distribution function of the hypergeometric distribution
- R.PLNORM — cumulative distribution function of the log-normal distribution
- R.PNBINOM — cumulative distribution function of the negative binomial distribution
- R.PNORM — cumulative distribution function of the normal distribution
- R.PPOIS — cumulative distribution function of the Poisson distribution
- R.PRAYLEIGH — cumulative distribution function of the Rayleigh distribution
- R.PSNORM — cumulative distribution function of the skew-normal distribution
- R.PST — cumulative distribution function of the skew-t distribution
- R.PT — cumulative distribution function of the Student t distribution
- R.PTUKEY — cumulative distribution function of the Studentized range distribution
- R.PWEIBULL — cumulative distribution function of the Weibull distribution
- R.QBETA — probability quantile function of the beta distribution
- R.QBINOM — probability quantile function of the binomial distribution
- R.QCAUCHY — probability quantile function of the Cauchy distribution
- R.QCHISQ — probability quantile function of the chi-square distribution
- R.QEXP — probability quantile function of the exponential distribution
- R.QF — probability quantile function of the F distribution
- R.QGAMMA — probability quantile function of the gamma distribution
- R.QGEOM — probability quantile function of the geometric distribution
- R.QGUMBEL — probability quantile function of the Gumbel distribution
- R.QHYPER — probability quantile function of the hypergeometric distribution
- R.QLNORM — probability quantile function of the log-normal distribution
- R.QNBINOM — probability quantile function of the negative binomial distribution
- R.QNORM — probability quantile function of the normal distribution
- R.QPOIS — probability quantile function of the Poisson distribution
- R.QRAYLEIGH — probability quantile function of the Rayleigh distribution
- R.QSNORM — probability quantile function of the skew-normal distribution
- R.QST — probability quantile function of the skew-t distribution
- R.QT — probability quantile function of the Student t distribution
- R.QTUKEY — probability quantile function of the Studentized range distribution
- R.QWEIBULL — probability quantile function of the Weibull distribution
- RANK — rank of a number in a list of numbers
- RANK.AVG — rank of a number in a list of numbers
- RAYLEIGH — probability density function of the Rayleigh distribution
- RAYLEIGHTAIL — probability density function of the Rayleigh tail distribution
- RSQ — square of the Pearson correlation coefficient of the paired set of data
- SFTEST — Shapiro-Francia Test of Normality
- SKEW — unbiased estimate for skewness of a distribution
- SKEWP — population skewness of a data set
- SLOPE — the slope of a linear regression line
- SMALL — k-th smallest value in a data set
- SNORM.DIST.RANGE — probability of the standard normal distribution over an interval
- SSMEDIAN — median for grouped data
- STANDARDIZE — z-score of a value
- STDEV — sample standard deviation of the given sample
- STDEVA — sample standard deviation of the given sample
- STDEVP — population standard deviation of the given population
- STDEVPA — population standard deviation of an entire population
- STEYX — standard error of the predicted y-value in the regression
- SUBTOTAL — the subtotal of the given list of arguments
- TDIST — survival function of the Student t-distribution
- TINV — two tailed inverse of the Student t-distribution
- TREND — estimates future values of a given data set using a least squares approximation
- TRIMMEAN — mean of the interior of a data set
- TTEST — p-value for a hypothesis test comparing the means of two populations using the Student t-distribution
- VAR — sample variance of the given sample
- VARA — sample variance of the given sample
- VARP — variance of an entire population
- VARPA — variance of an entire population
- WEIBULL — probability density or cumulative distribution function of the Weibull distribution
- ZTEST — the probability of observing a sample mean as large as or larger than the mean of the given sample
ADTEST
Synopsis
ADTEST(x)
Arguments
x: array of sample values
Description
This function returns an array with the first row giving the p-value of the Anderson-Darling Test, the second row the test statistic of the test, and the third the number of observations in the sample.
Note
If there are less than 8 sample values, ADTEST returns #VALUE!
AVEDEV
Synopsis
AVEDEV(number1,number2,…)
Arguments
number1: first value
number2: second value
Microsoft Excel Compatibility
This function is Excel compatible.
See also
AVERAGE
Synopsis
AVERAGE(number1,number2,…)
Arguments
number1: first value
number2: second value
Microsoft Excel Compatibility
This function is Excel compatible.
AVERAGEA
Synopsis
AVERAGEA(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1). Note that empty cells are not counted.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
BERNOULLI
Synopsis
BERNOULLI(k,p)
Arguments
k: integer
p: probability of success
Note
If k != 0 and k != 1 this function returns a #NUM! error. If p < 0 or p > 1 this function returns a #NUM! error.
See also
BETA.DIST
Synopsis
BETA.DIST(x,alpha,beta,cumulative,a,b)
Arguments
x: number
alpha: scale parameter
beta: scale parameter
cumulative: whether to evaluate the density function or the cumulative distribution function
a: optional lower bound, defaults to 0
b: optional upper bound, defaults to 1
Note
If x < a or x > b this function returns a #NUM! error. If alpha <= 0 or beta <= 0, this function returns a #NUM! error. If a >= b this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
BETADIST
Synopsis
BETADIST(x,alpha,beta,a,b)
Arguments
x: number
alpha: scale parameter
beta: scale parameter
a: optional lower bound, defaults to 0
b: optional upper bound, defaults to 1
Note
If x < a or x > b this function returns a #NUM! error. If alpha <= 0 or beta <= 0, this function returns a #NUM! error. If a >= b this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
BETAINV
Synopsis
BETAINV(p,alpha,beta,a,b)
Arguments
p: probability
alpha: scale parameter
beta: scale parameter
a: optional lower bound, defaults to 0
b: optional upper bound, defaults to 1
Note
If p < 0 or p > 1 this function returns a #NUM! error. If alpha <= 0 or beta <= 0, this function returns a #NUM! error. If a >= b this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
BINOM.DIST.RANGE
Synopsis
BINOM.DIST.RANGE(trials,p,start,end)
Arguments
trials: number of trials
p: probability of success in each trial
start: start of the interval
end: end of the interval, defaults to start
Note
If start, end or trials are non-integer they are truncated. If trials < 0 this function returns a #NUM! error. If p < 0 or p > 1 this function returns a #NUM! error. If start > end this function returns 0.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
BINOMDIST
Synopsis
BINOMDIST(n,trials,p,cumulative)
Arguments
n: number of successes
trials: number of trials
p: probability of success in each trial
cumulative: whether to evaluate the mass function or the cumulative distribution function
Note
If n or trials are non-integer they are truncated. If n < 0 or trials < 0 this function returns a #NUM! error. If n > trials this function returns a #NUM! error. If p < 0 or p > 1 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
CAUCHY
Synopsis
CAUCHY(x,a,cumulative)
Arguments
x: number
a: scale parameter
cumulative: whether to evaluate the density function or the cumulative distribution function
Note
If a < 0 this function returns a #NUM! error. If cumulative is neither TRUE nor FALSE this function returns a #VALUE! error.
See also
CHIDIST
Synopsis
CHIDIST(x,dof)
Arguments
x: number
dof: number of degrees of freedom
Description
The survival function is 1 minus the cumulative distribution function.
Note
If dof is non-integer it is truncated. If dof < 1 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
CHIDIST(x,dof) is the OpenFormula function LEGACY.CHIDIST(x,dof).
CHIINV
Synopsis
CHIINV(p,dof)
Arguments
p: probability
dof: number of degrees of freedom
Description
The survival function is 1 minus the cumulative distribution function.
Note
If p < 0 or p > 1 or dof < 1 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
CHIINV(p,dof) is the OpenFormula function LEGACY.CHIDIST(p,dof).
CHITEST
Synopsis
CHITEST(actual_range,theoretical_range)
Arguments
actual_range: observed data
theoretical_range: expected values
Note
If the actual range is not an n by 1 or 1 by n range, but an n by m range, then CHITEST uses (n-1) times (m-1) as degrees of freedom. This is useful if the expected values were calculated from the observed value in a test of independence or test of homogeneity.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
CHITEST is the OpenFormula function LEGACY.CHITEST.
CONFIDENCE
Synopsis
CONFIDENCE(alpha,stddev,size)
Arguments
alpha: significance level
stddev: population standard deviation
size: sample size
Note
This function requires the usually unknown population standard deviation. If size is non-integer it is truncated. If size < 0 this function returns a #NUM! error. If size is 0 this function returns a #DIV/0! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
CONFIDENCE.T
Synopsis
CONFIDENCE.T(alpha,stddev,size)
Arguments
alpha: significance level
stddev: sample standard deviation
size: sample size
Note
If stddev < 0 or = 0 this function returns a #NUM! error. If size is non-integer it is truncated. If size < 1 this function returns a #NUM! error. If size is 1 this function returns a #DIV/0! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
CORREL
Synopsis
CORREL(array1,array2)
Arguments
array1: first data set
array2: second data set
Description
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
COUNT
Synopsis
COUNT(number1,number2,…)
Arguments
number1: first value
number2: second value
Microsoft Excel Compatibility
This function is Excel compatible.
See also
COUNTA
Synopsis
COUNTA(number1,number2,…)
Arguments
number1: first value
number2: second value
Microsoft Excel Compatibility
This function is Excel compatible.
COVAR
Synopsis
COVAR(array1,array2)
Arguments
array1: first data set
array2: set data set
Description
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
COVARIANCE.S
Synopsis
COVARIANCE.S(array1,array2)
Arguments
array1: first data set
array2: set data set
Description
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
CRITBINOM
Synopsis
CRITBINOM(trials,p,alpha)
Arguments
trials: number of trials
p: probability of success in each trial
alpha: significance level (area of the tail)
Note
If trials is a non-integer it is truncated. If trials < 0 this function returns a #NUM! error. If p < 0 or p > 1 this function returns a #NUM! error. If alpha < 0 or alpha > 1 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
CRONBACH
Synopsis
CRONBACH(ref1,ref2,…)
Arguments
ref1: first data set
ref2: second data set
See also
VAR.
CVMTEST
Synopsis
CVMTEST(x)
Arguments
x: array of sample values
Description
This function returns an array with the first row giving the p-value of the Cramér-von Mises Test, the second row the test statistic of the test, and the third the number of observations in the sample.
Note
If there are less than 8 sample values, CVMTEST returns #VALUE!
DEVSQ
Synopsis
DEVSQ(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
EXPONDIST
Synopsis
EXPONDIST(x,y,cumulative)
Arguments
x: number
y: scale parameter
cumulative: whether to evaluate the density function or the cumulative distribution function
Description
If cumulative is false it will return: y * exp (-y*x), otherwise it will return 1 - exp (-y*x).
Note
If x < 0 or y <= 0 this will return an error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
EXPPOWDIST
Synopsis
EXPPOWDIST(x,a,b)
Arguments
x: number
a: scale parameter
b: scale parameter
Description
This distribution has been recommended for lifetime analysis when a U-shaped hazard function is desired. This corresponds to rapid failure once the product starts to wear out after a period of steady or even improving reliability.
See also
FDIST
Synopsis
FDIST(x,dof_of_num,dof_of_denom)
Arguments
x: number
dof_of_num: numerator degrees of freedom
dof_of_denom: denominator degrees of freedom
Description
The survival function is 1 minus the cumulative distribution function.
Note
If x < 0 this function returns a #NUM! error. If dof_of_num < 1 or dof_of_denom < 1, this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
FDIST is the OpenFormula function LEGACY.FDIST.
See also
FINV.
FINV
Synopsis
FINV(p,dof_of_num,dof_of_denom)
Arguments
p: probability
dof_of_num: numerator degrees of freedom
dof_of_denom: denominator degrees of freedom
Description
The survival function is 1 minus the cumulative distribution function.
Note
If p < 0 or p > 1 this function returns a #NUM! error. If dof_of_num < 1 or dof_of_denom < 1 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
FINV is the OpenFormula function LEGACY.FINV.
See also
FISHER
Synopsis
FISHER(x)
Arguments
x: number
Note
If x is not a number, this function returns a #VALUE! error. If x <= -1 or x >= 1, this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
FISHERINV
Synopsis
FISHERINV(x)
Arguments
x: number
Note
If x is a non-number this function returns a #VALUE! error.
Microsoft Excel Compatibility
This function is Excel compatible.
FORECAST
Synopsis
FORECAST(x,known_ys,known_xs)
Arguments
x: x-value whose matching y-value should be forecast
known_ys: known y-values
known_xs: known x-values
Description
This function estimates a future value according to existing values using simple linear regression.
Note
If known_xs or known_ys contains no data entries or different number of data entries, this function returns a #N/A error. If the variance of the known_xs is zero, this function returns a #DIV/0 error.
Microsoft Excel Compatibility
This function is Excel compatible.
FREQUENCY
Synopsis
FREQUENCY(data_array,bins_array)
Arguments
data_array: data values
bins_array: array of cutoff values
Description
The results are given as an array.
If the bins_array is empty, this function returns the number of data points in data_array.
Microsoft Excel Compatibility
This function is Excel compatible.
FTEST
Synopsis
FTEST(array1,array2)
Arguments
array1: sample from the first population
array2: sample from the second population
Microsoft Excel Compatibility
This function is Excel compatible.
GAMMADIST
Synopsis
GAMMADIST(x,alpha,beta,cumulative)
Arguments
x: number
alpha: scale parameter
beta: scale parameter
cumulative: whether to evaluate the density function or the cumulative distribution function
Note
If x < 0 this function returns a #NUM! error. If alpha <= 0 or beta <= 0, this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
GAMMAINV
Synopsis
GAMMAINV(p,alpha,beta)
Arguments
p: probability
alpha: scale parameter
beta: scale parameter
Note
If p < 0 or p > 1 this function returns a #NUM! error. If alpha <= 0 or beta <= 0 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
GEOMDIST
Synopsis
GEOMDIST(k,p,cumulative)
Arguments
k: number of trials
p: probability of success in any trial
cumulative: whether to evaluate the mass function or the cumulative distribution function
Note
If k < 0 this function returns a #NUM! error. If p < 0 or p > 1 this function returns a #NUM! error. If cumulative is neither TRUE nor FALSE this function returns a #VALUE! error.
See also
GEOMEAN
Synopsis
GEOMEAN(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
The geometric mean is equal to the Nth root of the product of the N values.
Microsoft Excel Compatibility
This function is Excel compatible.
GROWTH
Synopsis
GROWTH(known_ys,known_xs,new_xs,affine)
Arguments
known_ys: known y-values
known_xs: known x-values; defaults to the array {1, 2, 3, …}
new_xs: x-values for which to estimate the y-values; defaults to known_xs
affine: if true, the model contains a constant term, defaults to true
Description
GROWTH function applies the “least squares” method to fit an exponential curve to your data and predicts the exponential growth by using this curve.
GROWTH returns an array having one column and a row for each data point in new_xs.
Note
If known_ys and known_xs have unequal number of data points, this function returns a #NUM! error.
HARMEAN
Synopsis
HARMEAN(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
The harmonic mean of N data points is N divided by the sum of the reciprocals of the data points).
Microsoft Excel Compatibility
This function is Excel compatible.
HYPGEOMDIST
Synopsis
HYPGEOMDIST(x,n,M,N,cumulative)
Arguments
x: number of successes
n: sample size
M: number of possible successes in the population
N: population size
cumulative: whether to evaluate the mass function or the cumulative distribution function
Note
If x,n,M or N is a non-integer it is truncated. If x,n,M or N < 0 this function returns a #NUM! error. If x > M or n > N this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
INTERCEPT
Synopsis
INTERCEPT(known_ys,known_xs)
Arguments
known_ys: known y-values
known_xs: known x-values
Note
If known_xs or known_ys contains no data entries or different number of data entries, this function returns a #N/A error. If the variance of the known_xs is zero, this function returns #DIV/0 error.
Microsoft Excel Compatibility
This function is Excel compatible.
KURT
Synopsis
KURT(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
Note
This is only meaningful if the underlying distribution really has a fourth moment. The kurtosis is offset by three such that a normal distribution will have zero kurtosis. If fewer than four numbers are given or all of them are equal this function returns a #DIV/0! error.
Microsoft Excel Compatibility
This function is Excel compatible.
KURTP
Synopsis
KURTP(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
Note
If fewer than two numbers are given or all of them are equal this function returns a #DIV/0! error.
LANDAU
Synopsis
LANDAU(x)
Arguments
x: number
See also
LAPLACE
Synopsis
LAPLACE(x,a)
Arguments
x: number
a: mean
See also
LARGE
Synopsis
LARGE(data,k)
Arguments
data: data set
k: which value to find
Note
If data set is empty this function returns a #NUM! error. If k <= 0 or k is greater than the number of data items given this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
LEVERAGE
Synopsis
LEVERAGE(A)
Arguments
A: a matrix
Description
Returns the diagonal of A (A^T A)^-1 A^T as a column vector.
Note
If the matrix is singular, #VALUE! is returned.
LINEST
Synopsis
LINEST(known_ys,known_xs,affine,stats)
Arguments
known_ys: vector of values of dependent variable
known_xs: array of values of independent variables, defaults to a single vector {1,…,n}
affine: if true, the model contains a constant term, defaults to true
stats: if true, some additional statistics are provided, defaults to false
Description
This function returns an array with the first row giving the regression coefficients for the independent variables x_m, x_(m-1),…,x_2, x_1 followed by the y-intercept if affine is true.
If stats is true, the second row contains the corresponding standard errors of the regression coefficients. In this case, the third row contains the R^2 value and the standard error for the predicted value. The fourth row contains the observed F value and its degrees of freedom. Finally, the fifth row contains the regression sum of squares and the residual sum of squares.
If affine is false, R^2 is the uncentered version of the coefficient of determination; that is the proportion of the sum of squares explained by the model.
Note
If the length of known_ys does not match the corresponding length of known_xs, this function returns a #NUM! error.
LKSTEST
Synopsis
LKSTEST(x)
Arguments
x: array of sample values
Description
This function returns an array with the first row giving the p-value of the Lilliefors (Kolmogorov-Smirnov) Test, the second row the test statistic of the test, and the third the number of observations in the sample.
Note
If there are less than 5 sample values, LKSTEST returns #VALUE!
LOGEST
Synopsis
LOGEST(known_ys,known_xs,affine,stat)
Arguments
known_ys: known y-values
known_xs: known x-values; default to an array {1, 2, 3, …}
affine: if true, the model contains a constant term, defaults to true
stat: if true, extra statistical information will be returned; defaults to FALSE
Description
LOGEST function applies the “least squares” method to fit an exponential curve of the form y = b * m{1}^x{1} * m{2}^x{2}... to your data.
LOGEST returns an array { m{n},m{n-1}, ...,m{1},b }.
Note
Extra statistical information is written below the regression line coefficients in the result array. Extra statistical information consists of four rows of data. In the first row the standard error values for the coefficients m1, (m2, ...), b are represented. The second row contains the square of R and the standard error for the y estimate. The third row contains the F-observed value and the degrees of freedom. The last row contains the regression sum of squares and the residual sum of squares. If known_ys and known_xs have unequal number of data points, this function returns a #NUM! error.
LOGFIT
Synopsis
LOGFIT(known_ys,known_xs)
Arguments
known_ys: known y-values
known_xs: known x-values
Description
LOGFIT function applies the “least squares” method to fit the logarithmic equation y = a + b * ln(sign * (x - c)) , sign = +1 or -1 to your data. The graph of the equation is a logarithmic curve moved horizontally by c and possibly mirrored across the y-axis (if sign = -1).
LOGFIT returns an array having five columns and one row. `Sign' is given in the first column, `a', `b', and `c' are given in columns 2 to 4. Column 5 holds the sum of squared residuals.
Note
An error is returned when there are less than 3 different x's or y's, or when the shape of the point cloud is too different from a ``logarithmic'' one. You can use the above formula = a + b * ln(sign * (x - c)) or rearrange it to = (exp((y - a) / b)) / sign + c to compute unknown y's or x's, respectively. This is non-linear fitting by trial-and-error. The accuracy of `c' is: width of x-range -> rounded to the next smaller (10^integer), times 0.000001. There might be cases in which the returned fit is not the best possible.
LOGINV
Synopsis
LOGINV(p,mean,stddev)
Arguments
p: probability
mean: mean
stddev: standard deviation
Note
If p < 0 or p > 1 or stddev <= 0 this function returns #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
EXP, LN, LOG, LOG10, LOGNORMDIST.
LOGISTIC
Synopsis
LOGISTIC(x,a)
Arguments
x: number
a: scale parameter
See also
LOGNORMDIST
Synopsis
LOGNORMDIST(x,mean,stddev)
Arguments
x: number
mean: mean
stddev: standard deviation
Note
If stddev = 0 LOGNORMDIST returns a #DIV/0! error. If x <= 0, mean < 0 or stddev <= 0 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
LOGREG
Synopsis
LOGREG(known_ys,known_xs,affine,stat)
Arguments
known_ys: known y-values
known_xs: known x-values; defaults to the array {1, 2, 3, …}
affine: if true, the model contains a constant term, defaults to true
stat: if true, extra statistical information will be returned; defaults to FALSE
Description
LOGREG function transforms your x's to z=ln(x) and applies the “least squares” method to fit the linear equation y = m * z + b to your y's and z's --- equivalent to fitting the equation y = m * ln(x) + b to y's and x's. LOGREG returns an array having two columns and one row. m is given in the first column and b in the second.
Any extra statistical information is written below m and b in the result array. This extra statistical information consists of four rows of data: In the first row the standard error values for the coefficients m, b are given. The second row contains the square of R and the standard error for the y estimate. The third row contains the F-observed value and the degrees of freedom. The last row contains the regression sum of squares and the residual sum of squares. The default of stat is FALSE.
Note
If known_ys and known_xs have unequal number of data points, this function returns a #NUM! error.
MAX
Synopsis
MAX(number1,number2,…)
Arguments
number1: first value
number2: second value
Microsoft Excel Compatibility
This function is Excel compatible.
MAXA
Synopsis
MAXA(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1). Note that empty cells are not counted.
Microsoft Excel Compatibility
This function is Excel compatible.
MEDIAN
Synopsis
MEDIAN(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
Note
If even numbers are given MEDIAN returns the average of the two numbers in the center.
Microsoft Excel Compatibility
This function is Excel compatible.
MIN
Synopsis
MIN(number1,number2,…)
Arguments
number1: first value
number2: second value
Microsoft Excel Compatibility
This function is Excel compatible.
MINA
Synopsis
MINA(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1). Note that empty cells are not counted.
Microsoft Excel Compatibility
This function is Excel compatible.
MODE
Synopsis
MODE(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
If the data set does not contain any duplicates this function returns a #N/A error.
Microsoft Excel Compatibility
This function is Excel compatible.
MODE.MULT
Synopsis
MODE.MULT(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
If the data set does not contain any duplicates this function returns a #N/A error.
Microsoft Excel Compatibility
This function is Excel compatible.
NEGBINOMDIST
Synopsis
NEGBINOMDIST(f,t,p)
Arguments
f: number of failures
t: threshold number of successes
p: probability of a success
Note
If f or t is a non-integer it is truncated. If (f + t -1) <= 0 this function returns a #NUM! error. If p < 0 or p > 1 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
BINOMDIST, COMBIN, FACT, HYPGEOMDIST, PERMUT.
NORMDIST
Synopsis
NORMDIST(x,mean,stddev,cumulative)
Arguments
x: number
mean: mean of the distribution
stddev: standard deviation of the distribution
cumulative: whether to evaluate the density function or the cumulative distribution function
Note
If stddev is 0 this function returns a #DIV/0! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
NORMINV
Synopsis
NORMINV(p,mean,stddev)
Arguments
p: probability
mean: mean of the distribution
stddev: standard deviation of the distribution
Note
If p < 0 or p > 1 or stddev <= 0 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
NORMSDIST
Synopsis
NORMSDIST(x)
Arguments
x: number
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
NORMSDIST is the OpenFormula function LEGACY.NORMSDIST.
See also
NORMSINV
Synopsis
NORMSINV(p)
Arguments
p: given probability
Note
If p < 0 or p > 1 this function returns #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
NORMSINV is the OpenFormula function LEGACY.NORMSINV.
See also
PARETO
Synopsis
PARETO(x,a,b)
Arguments
x: number
a: exponent
b: scale parameter
See also
PEARSON
Synopsis
PEARSON(array1,array2)
Arguments
array1: first component values
array2: second component values
Description
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
PERCENTILE
Synopsis
PERCENTILE(array,k)
Arguments
array: data points
k: which percentile to calculate
Note
If array is empty, this function returns a #NUM! error. If k < 0 or k > 1, this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
PERCENTILE.EXC
Synopsis
PERCENTILE.EXC(array,k)
Arguments
array: data points
k: which percentile to calculate
Note
If array is empty, this function returns a #NUM! error. If k < 0 or k > 1, this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
PERCENTRANK
Synopsis
PERCENTRANK(array,x,significance)
Arguments
array: range of numeric values
x: data point to be ranked
significance: number of significant digits, defaults to 3
Note
If array contains no data points, this function returns a #NUM! error. If significance is less than one, this function returns a #NUM! error. If x exceeds the largest value or is less than the smallest value in array, this function returns an #N/A error. If x does not match any of the values in array or x matches more than once, this function interpolates the returned value.
PERCENTRANK.EXC
Synopsis
PERCENTRANK.EXC(array,x,significance)
Arguments
array: range of numeric values
x: data point to be ranked
significance: number of significant digits, defaults to 3
Note
If array contains no data points, this function returns a #NUM! error. If significance is less than one, this function returns a #NUM! error. If x exceeds the largest value or is less than the smallest value in array, this function returns an #N/A error. If x does not match any of the values in array or x matches more than once, this function interpolates the returned value.
See also
LARGE, MAX, MEDIAN, MIN, PERCENTILE, PERCENTILE.EXC, QUARTILE, QUARTILE.EXC, SMALL.
PERMUT
Synopsis
PERMUT(n,k)
Arguments
n: size of the base set
k: number of elements in each permutation
Note
If n = 0 this function returns a #NUM! error. If n < k this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
PERMUTATIONA
Synopsis
PERMUTATIONA(x,y)
Arguments
x: total number of objects
y: number of selected objects
Note
If both x and y equal 0, PERMUTATIONA returns 1. If x < 0 or y < 0, PERMUTATIONA returns #NUM! If x or y are not integers, they are truncated.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
POISSON
Synopsis
POISSON(x,mean,cumulative)
Arguments
x: number of events
mean: mean of the distribution
cumulative: whether to evaluate the mass function or the cumulative distribution function
Note
If x is a non-integer it is truncated. If x < 0 this function returns a #NUM! error. If mean <= 0 POISSON returns the #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
PROB
Synopsis
PROB(x_range,prob_range,lower_limit,upper_limit)
Arguments
x_range: possible values
prob_range: probabilities of the corresponding values
lower_limit: lower interval limit
upper_limit: upper interval limit, defaults to lower_limit
Note
If the sum of the probabilities in prob_range is not equal to 1 this function returns a #NUM! error. If any value in prob_range is <=0 or > 1, this function returns a #NUM! error. If x_range and prob_range contain a different number of data entries, this function returns a #N/A error.
Microsoft Excel Compatibility
This function is Excel compatible.
QUARTILE
Synopsis
QUARTILE(array,quart)
Arguments
array: data points
quart: a number from 0 to 4, indicating which quartile to calculate
Note
If array is empty, this function returns a #NUM! error. If quart < 0 or quart > 4, this function returns a #NUM! error. If quart = 0, the smallest value of array to be returned. If quart is not an integer, it is truncated.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
LARGE, MAX, MEDIAN, MIN, PERCENTILE, QUARTILE.EXC, SMALL.
QUARTILE.EXC
Synopsis
QUARTILE.EXC(array,quart)
Arguments
array: data points
quart: a number from 1 to 3, indicating which quartile to calculate
Note
If array is empty, this function returns a #NUM! error. If quart < 0 or quart > 4, this function returns a #NUM! error. If quart = 0, the smallest value of array to be returned. If quart is not an integer, it is truncated.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
LARGE, MAX, MEDIAN, MIN, PERCENTILE, PERCENTILE.EXC, QUARTILE, SMALL.
R.DBETA
Synopsis
R.DBETA(x,a,b,give_log)
Arguments
x: observation
a: the first shape parameter of the distribution
b: the second scale parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the beta distribution.
R.DBINOM
Synopsis
R.DBINOM(x,n,psuc,give_log)
Arguments
x: observation
n: the number of trials
psuc: the probability of success in each trial
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the binomial distribution.
R.DCAUCHY
Synopsis
R.DCAUCHY(x,location,scale,give_log)
Arguments
x: observation
location: the center of the distribution
scale: the scale parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the Cauchy distribution.
R.DCHISQ
Synopsis
R.DCHISQ(x,df,give_log)
Arguments
x: observation
df: the number of degrees of freedom of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the chi-square distribution.
OpenDocument Format (ODF) Compatibility
A two argument invocation R.DCHISQ(x,df) is exported to OpenFormula as CHISQDIST(x,df,FALSE()).
R.DEXP
Synopsis
R.DEXP(x,scale,give_log)
Arguments
x: observation
scale: the scale parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the exponential distribution.
R.DF
Synopsis
R.DF(x,n1,n2,give_log)
Arguments
x: observation
n1: the first number of degrees of freedom of the distribution
n2: the second number of degrees of freedom of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the F distribution.
R.DGAMMA
Synopsis
R.DGAMMA(x,shape,scale,give_log)
Arguments
x: observation
shape: the shape parameter of the distribution
scale: the scale parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the gamma distribution.
R.DGEOM
Synopsis
R.DGEOM(x,psuc,give_log)
Arguments
x: observation
psuc: the probability of success in each trial
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the geometric distribution.
R.DGUMBEL
Synopsis
R.DGUMBEL(x,mu,beta,give_log)
Arguments
x: observation
mu: the location parameter of freedom of the distribution
beta: the scale parameter of freedom of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the Gumbel distribution.
R.DHYPER
Synopsis
R.DHYPER(x,r,b,n,give_log)
Arguments
x: observation
r: the number of red balls
b: the number of black balls
n: the number of balls drawn
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the hypergeometric distribution.
R.DLNORM
Synopsis
R.DLNORM(x,logmean,logsd,give_log)
Arguments
x: observation
logmean: mean of the underlying normal distribution
logsd: standard deviation of the underlying normal distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the log-normal distribution.
R.DNBINOM
Synopsis
R.DNBINOM(x,n,psuc,give_log)
Arguments
x: observation (number of failures)
n: required number of successes
psuc: the probability of success in each trial
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the negative binomial distribution.
R.DNORM
Synopsis
R.DNORM(x,mu,sigma,give_log)
Arguments
x: observation
mu: mean of the distribution
sigma: standard deviation of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the normal distribution.
R.DPOIS
Synopsis
R.DPOIS(x,lambda,give_log)
Arguments
x: observation
lambda: the mean of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the Poisson distribution.
R.DRAYLEIGH
Synopsis
R.DRAYLEIGH(x,scale,give_log)
Arguments
x: observation
scale: the scale parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the Rayleigh distribution.
See also
R.DSNORM
Synopsis
R.DSNORM(x,shape,location,scale,give_log)
Arguments
x: observation
shape: the shape parameter of the distribution
location: the location parameter of the distribution
scale: the scale parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the skew-normal distribution.
R.DST
Synopsis
R.DST(x,n,shape,give_log)
Arguments
x: observation
n: the number of degrees of freedom of the distribution
shape: the shape parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the skew-t distribution.
R.DT
Synopsis
R.DT(x,n,give_log)
Arguments
x: observation
n: the number of degrees of freedom of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the Student t distribution.
R.DWEIBULL
Synopsis
R.DWEIBULL(x,shape,scale,give_log)
Arguments
x: observation
shape: the shape parameter of the distribution
scale: the scale parameter of the distribution
give_log: if true, log of the result will be returned instead
Description
This function returns the probability density function of the Weibull distribution.
See also
R.PBETA
Synopsis
R.PBETA(x,a,b,lower_tail,log_p)
Arguments
x: observation
a: the first shape parameter of the distribution
b: the second scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the beta distribution.
R.PBINOM
Synopsis
R.PBINOM(x,n,psuc,lower_tail,log_p)
Arguments
x: observation
n: the number of trials
psuc: the probability of success in each trial
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the binomial distribution.
R.PCAUCHY
Synopsis
R.PCAUCHY(x,location,scale,lower_tail,log_p)
Arguments
x: observation
location: the center of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the Cauchy distribution.
R.PCHISQ
Synopsis
R.PCHISQ(x,df,lower_tail,log_p)
Arguments
x: observation
df: the number of degrees of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the chi-square distribution.
OpenDocument Format (ODF) Compatibility
A two argument invocation R.PCHISQ(x,df) is exported to OpenFormula as CHISQDIST(x,df).
R.PEXP
Synopsis
R.PEXP(x,scale,lower_tail,log_p)
Arguments
x: observation
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the exponential distribution.
R.PF
Synopsis
R.PF(x,n1,n2,lower_tail,log_p)
Arguments
x: observation
n1: the first number of degrees of freedom of the distribution
n2: the second number of degrees of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the F distribution.
R.PGAMMA
Synopsis
R.PGAMMA(x,shape,scale,lower_tail,log_p)
Arguments
x: observation
shape: the shape parameter of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the gamma distribution.
R.PGEOM
Synopsis
R.PGEOM(x,psuc,lower_tail,log_p)
Arguments
x: observation
psuc: the probability of success in each trial
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the geometric distribution.
R.PGUMBEL
Synopsis
R.PGUMBEL(x,mu,beta,lower_tail,log_p)
Arguments
x: observation
mu: the location parameter of freedom of the distribution
beta: the scale parameter of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the Gumbel distribution.
R.PHYPER
Synopsis
R.PHYPER(x,r,b,n,lower_tail,log_p)
Arguments
x: observation
r: the number of red balls
b: the number of black balls
n: the number of balls drawn
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the hypergeometric distribution.
R.PLNORM
Synopsis
R.PLNORM(x,logmean,logsd,lower_tail,log_p)
Arguments
x: observation
logmean: mean of the underlying normal distribution
logsd: standard deviation of the underlying normal distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the log-normal distribution.
R.PNBINOM
Synopsis
R.PNBINOM(x,n,psuc,lower_tail,log_p)
Arguments
x: observation (number of failures)
n: required number of successes
psuc: the probability of success in each trial
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the negative binomial distribution.
R.PNORM
Synopsis
R.PNORM(x,mu,sigma,lower_tail,log_p)
Arguments
x: observation
mu: mean of the distribution
sigma: standard deviation of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the normal distribution.
R.PPOIS
Synopsis
R.PPOIS(x,lambda,lower_tail,log_p)
Arguments
x: observation
lambda: the mean of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the Poisson distribution.
R.PRAYLEIGH
Synopsis
R.PRAYLEIGH(x,scale,lower_tail,log_p)
Arguments
x: observation
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the Rayleigh distribution.
See also
R.PSNORM
Synopsis
R.PSNORM(x,shape,location,scale,lower_tail,log_p)
Arguments
x: observation
shape: the shape parameter of the distribution
location: the location parameter of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the skew-normal distribution.
R.PST
Synopsis
R.PST(x,n,shape,lower_tail,log_p)
Arguments
x: observation
n: the number of degrees of freedom of the distribution
shape: the shape parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the skew-t distribution.
R.PT
Synopsis
R.PT(x,n,lower_tail,log_p)
Arguments
x: observation
n: the number of degrees of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the Student t distribution.
R.PTUKEY
Synopsis
R.PTUKEY(x,nmeans,df,nranges,lower_tail,log_p)
Arguments
x: observation
nmeans: the number of means
df: the number of degrees of freedom of the distribution
nranges: the number of ranges; default is 1
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the Studentized range distribution.
See also
R.PWEIBULL
Synopsis
R.PWEIBULL(x,shape,scale,lower_tail,log_p)
Arguments
x: observation
shape: the shape parameter of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the cumulative distribution function of the Weibull distribution.
See also
R.QBETA
Synopsis
R.QBETA(p,a,b,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
a: the first shape parameter of the distribution
b: the second scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the beta distribution.
R.QBINOM
Synopsis
R.QBINOM(p,n,psuc,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
n: the number of trials
psuc: the probability of success in each trial
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the binomial distribution.
R.QCAUCHY
Synopsis
R.QCAUCHY(p,location,scale,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
location: the center of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the Cauchy distribution.
R.QCHISQ
Synopsis
R.QCHISQ(p,df,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
df: the number of degrees of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the chi-square distribution.
OpenDocument Format (ODF) Compatibility
A two argument invocation R.QCHISQ(p,df) is exported to OpenFormula as CHISQINV(p,df).
R.QEXP
Synopsis
R.QEXP(p,scale,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the exponential distribution.
R.QF
Synopsis
R.QF(p,n1,n2,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
n1: the first number of degrees of freedom of the distribution
n2: the second number of degrees of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the F distribution.
R.QGAMMA
Synopsis
R.QGAMMA(p,shape,scale,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
shape: the shape parameter of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the gamma distribution.
R.QGEOM
Synopsis
R.QGEOM(p,psuc,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
psuc: the probability of success in each trial
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the geometric distribution.
R.QGUMBEL
Synopsis
R.QGUMBEL(p,mu,beta,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
mu: the location parameter of freedom of the distribution
beta: the scale parameter of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the Gumbel distribution.
R.QHYPER
Synopsis
R.QHYPER(p,r,b,n,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
r: the number of red balls
b: the number of black balls
n: the number of balls drawn
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the hypergeometric distribution.
R.QLNORM
Synopsis
R.QLNORM(p,logmean,logsd,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
logmean: mean of the underlying normal distribution
logsd: standard deviation of the underlying normal distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the log-normal distribution.
R.QNBINOM
Synopsis
R.QNBINOM(p,n,psuc,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
n: required number of successes
psuc: the probability of success in each trial
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the negative binomial distribution.
R.QNORM
Synopsis
R.QNORM(p,mu,sigma,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
mu: mean of the distribution
sigma: standard deviation of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the normal distribution.
R.QPOIS
Synopsis
R.QPOIS(p,lambda,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
lambda: the mean of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the Poisson distribution.
R.QRAYLEIGH
Synopsis
R.QRAYLEIGH(p,scale,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the Rayleigh distribution.
See also
R.QSNORM
Synopsis
R.QSNORM(p,shape,location,scale,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
shape: the shape parameter of the distribution
location: the location parameter of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the skew-normal distribution.
R.QST
Synopsis
R.QST(p,n,shape,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
n: the number of degrees of freedom of the distribution
shape: the shape parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the skew-t distribution.
R.QT
Synopsis
R.QT(p,n,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
n: the number of degrees of freedom of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the Student t distribution.
R.QTUKEY
Synopsis
R.QTUKEY(p,nmeans,df,nranges,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
nmeans: the number of means
df: the number of degrees of freedom of the distribution
nranges: the number of ranges; default is 1
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the Studentized range distribution.
See also
R.QWEIBULL
Synopsis
R.QWEIBULL(p,shape,scale,lower_tail,log_p)
Arguments
p: probability or natural logarithm of the probability
shape: the shape parameter of the distribution
scale: the scale parameter of the distribution
lower_tail: if true (the default), the lower tail of the distribution is considered
log_p: if true, the natural logarithm of the probability is given or returned; defaults to false
Description
This function returns the probability quantile function, i.e., the inverse of the cumulative distribution function, of the Weibull distribution.
See also
RANK
Synopsis
RANK(x,ref,order)
Arguments
x: number whose rank you want to find
ref: list of numbers
order: 0 (descending order) or non-zero (ascending order); defaults to 0
Note
In case of a tie, RANK returns the largest possible rank.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
RANK.AVG
Synopsis
RANK.AVG(x,ref,order)
Arguments
x: number whose rank you want to find
ref: list of numbers
order: 0 (descending order) or non-zero (ascending order); defaults to 0
Note
In case of a tie, RANK.AVG returns the average rank.
Microsoft Excel Compatibility
This function is Excel 2010 compatible.
See also
RAYLEIGH
Synopsis
RAYLEIGH(x,sigma)
Arguments
x: number
sigma: scale parameter
See also
RAYLEIGHTAIL
Synopsis
RAYLEIGHTAIL(x,a,sigma)
Arguments
x: number
a: lower limit
sigma: scale parameter
See also
RSQ
Synopsis
RSQ(array1,array2)
Arguments
array1: first component values
array2: second component values
Description
Strings and empty cells are simply ignored.
Microsoft Excel Compatibility
This function is Excel compatible.
SFTEST
Synopsis
SFTEST(x)
Arguments
x: array of sample values
Description
This function returns an array with the first row giving the p-value of the Shapiro-Francia Test, the second row the test statistic of the test, and the third the number of observations in the sample.
Note
If there are less than 5 or more than 5000 sample values, SFTEST returns #VALUE!
SKEW
Synopsis
SKEW(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
Note
This is only meaningful if the underlying distribution really has a third moment. The skewness of a symmetric (e.g., normal) distribution is zero. If less than three numbers are given, this function returns a #DIV/0! error.
Microsoft Excel Compatibility
This function is Excel compatible.
SKEWP
Synopsis
SKEWP(number1,number2,…)
Arguments
number1: first value
number2: second value
Description
Strings and empty cells are simply ignored.
Note
If less than two numbers are given, SKEWP returns a #DIV/0! error.
SLOPE
Synopsis
SLOPE(known_ys,known_xs)
Arguments
known_ys: known y-values
known_xs: known x-values
Note
If known_xs or known_ys contains no data entries or different number of data entries, this function returns a #N/A error. If the variance of the known_xs is zero, this function returns #DIV/0 error.
Microsoft Excel Compatibility
This function is Excel compatible.
SMALL
Synopsis
SMALL(data,k)
Arguments
data: data set
k: which value to find
Note
If data set is empty this function returns a #NUM! error. If k <= 0 or k is greater than the number of data items given this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
SNORM.DIST.RANGE
Synopsis
SNORM.DIST.RANGE(x1,x2)
Arguments
x1: start of the interval
x2: end of the interval
Description
This function returns the cumulative probability over a range of the standard normal distribution; that is the integral over the probability density function from x1 to x2.
Note
If x1>x2, this function returns a negative value.
SSMEDIAN
Synopsis
SSMEDIAN(array,interval)
Arguments
array: data set
interval: length of each grouping interval, defaults to 1
Description
The data are assumed to be grouped into intervals of width interval. Each data point in array is the midpoint of the interval containing the true value. The median is calculated by interpolation within the median interval (the interval containing the median value), assuming that the true values within that interval are distributed uniformly:
median = L + interval*(N/2 - CF)/F
where:
L = the lower limit of the median interval
N = the total number of data points
CF = the number of data points below the median interval
F = the number of data points in the median interval
Note
If array is empty, this function returns a #NUM! error. If interval <= 0, this function returns a #NUM! error. SSMEDIAN does not check whether the data points are at least interval apart.
See also
STANDARDIZE
Synopsis
STANDARDIZE(x,mean,stddev)
Arguments
x: value
mean: mean of the original distribution
stddev: standard deviation of the original distribution
Note
If stddev is 0 this function returns a #DIV/0! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
STDEV
Synopsis
STDEV(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
STDEV is also known as the N-1-standard deviation.
To obtain the population standard deviation of a whole population use STDEVP.
Microsoft Excel Compatibility
This function is Excel compatible.
STDEVA
Synopsis
STDEVA(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
STDEVA is also known as the N-1-standard deviation.
To obtain the population standard deviation of a whole population use STDEVPA.
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1). Note that empty cells are not counted.
Microsoft Excel Compatibility
This function is Excel compatible.
STDEVP
Synopsis
STDEVP(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
This is also known as the N-standard deviation
Microsoft Excel Compatibility
This function is Excel compatible.
STDEVPA
Synopsis
STDEVPA(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
This is also known as the N-standard deviation
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1). Note that empty cells are not counted.
Microsoft Excel Compatibility
This function is Excel compatible.
STEYX
Synopsis
STEYX(known_ys,known_xs)
Arguments
known_ys: known y-values
known_xs: known x-values
Note
If known_ys and known_xs are empty or have a different number of arguments then this function returns a #N/A error.
Microsoft Excel Compatibility
This function is Excel compatible.
SUBTOTAL
Synopsis
SUBTOTAL(function_nbr,ref1,ref2,…)
Arguments
function_nbr: determines which function to use according to the following table:
1 AVERAGE
2 COUNT
3 COUNTA
4 MAX
5 MIN
6 PRODUCT
7 STDEV
8 STDEVP
9 SUM
10 VAR
11 VARP
ref1: first value
ref2: second value
Microsoft Excel Compatibility
This function is Excel compatible.
TDIST
Synopsis
TDIST(x,dof,tails)
Arguments
x: number
dof: number of degrees of freedom
tails: 1 or 2
Description
The survival function is 1 minus the cumulative distribution function.
This function is Excel compatible for non-negative x.
Note
If dof < 1 this function returns a #NUM! error. If tails is neither 1 or 2 this function returns a #NUM! error. The parameterization of this function is different from what is used for, e.g., NORMSDIST. This is a common source of mistakes, but necessary for compatibility.
TINV
Synopsis
TINV(p,dof)
Arguments
p: probability in both tails
dof: number of degrees of freedom
Description
This function returns the non-negative value x such that the area under the Student t density with dof degrees of freedom to the right of x is p/2.
Note
If p < 0 or p > 1 or dof < 1 this function returns a #NUM! error. The parameterization of this function is different from what is used for, e.g., NORMSINV. This is a common source of mistakes, but necessary for compatibility.
Microsoft Excel Compatibility
This function is Excel compatible.
TREND
Synopsis
TREND(known_ys,known_xs,new_xs,affine)
Arguments
known_ys: vector of values of dependent variable
known_xs: array of values of independent variables, defaults to a single vector {1,…,n}
new_xs: array of x-values for which to estimate the y-values; defaults to known_xs
affine: if true, the model contains a constant term, defaults to true
Note
If the length of known_ys does not match the corresponding length of known_xs, this function returns a #NUM! error.
See also
TRIMMEAN
Synopsis
TRIMMEAN(ref,fraction)
Arguments
ref: list of numbers whose mean you want to calculate
fraction: fraction of the data set excluded from the mean
Description
If fraction=0.2 and the data set contains 40 numbers, 8 numbers are trimmed from the data set (40 x 0.2): the 4 largest and the 4 smallest. To avoid a bias, the number of points to be excluded is always rounded down to the nearest even number.
Microsoft Excel Compatibility
This function is Excel compatible.
TTEST
Synopsis
TTEST(array1,array2,tails,type)
Arguments
array1: sample from the first population
array2: sample from the second population
tails: number of tails to consider
type: Type of test to perform. 1 indicates a test for paired variables, 2 a test of unpaired variables with equal variances, and 3 a test of unpaired variables with unequal variances
Note
If the data sets contain a different number of data points and the test is paired (type one), TTEST returns the #N/A error. tails and type are truncated to integers. If tails is not one or two, this function returns a #NUM! error. If type is any other than one, two, or three, this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
VAR
Synopsis
VAR(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
VAR is also known as the N-1-variance.
Note
Since the N-1-variance includes Bessel's correction, whereas the N-variance calculated by VARPA or VARP does not, under reasonable conditions the N-1-variance is an unbiased estimator of the variance of the population from which the sample is drawn.
Microsoft Excel Compatibility
This function is Excel compatible.
VARA
Synopsis
VARA(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
VARA is also known as the N-1-variance.
To get the true variance of a complete population use VARPA.
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1). Note that empty cells are not counted.
Note
Since the N-1-variance includes Bessel's correction, whereas the N-variance calculated by VARPA or VARP does not, under reasonable conditions the N-1-variance is an unbiased estimator of the variance of the population from which the sample is drawn.
Microsoft Excel Compatibility
This function is Excel compatible.
VARP
Synopsis
VARP(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
VARP is also known as the N-variance.
VARPA
Synopsis
VARPA(area1,area2,…)
Arguments
area1: first cell area
area2: second cell area
Description
VARPA is also known as the N-variance.
Numbers, text and logical values are included in the calculation too. If the cell contains text or the argument evaluates to FALSE, it is counted as value zero (0). If the argument evaluates to TRUE, it is counted as one (1). Note that empty cells are not counted.
Microsoft Excel Compatibility
This function is Excel compatible.
WEIBULL
Synopsis
WEIBULL(x,alpha,beta,cumulative)
Arguments
x: number
alpha: scale parameter
beta: scale parameter
cumulative: whether to evaluate the density function or the cumulative distribution function
Description
If the cumulative boolean is true it will return: 1 - exp (-(x/beta)^alpha), otherwise it will return (alpha/beta^alpha) * x^(alpha-1) * exp(-(x/beta^alpha)).
Note
If x < 0 this function returns a #NUM! error. If alpha <= 0 or beta <= 0 this function returns a #NUM! error.
Microsoft Excel Compatibility
This function is Excel compatible.
See also
ZTEST
Synopsis
ZTEST(ref,x,stddev)
Arguments
ref: data set (sample)
x: population mean
stddev: population standard deviation, defaults to the sample standard deviation
Description
ZTEST calculates the probability of observing a sample mean as large as or larger than the mean of the given sample for samples drawn from a normal distribution with mean x and standard deviation stddev.
Note
If ref contains less than two data items ZTEST returns #DIV/0! error.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
CONFIDENCE, NORMDIST, NORMINV, NORMSDIST, NORMSINV, STANDARDIZE.
A.16. String
- ASC — text with full-width katakana and ASCII characters converted to half-width
- CHAR — the CP1252 (Windows-1252) character for the code point x
- CLEAN — text with any non-printable characters removed
- CODE — the CP1252 (Windows-1252) code point for the character c
- CONCAT — the concatenation of the strings s1, s2,…
- CONCATENATE — the concatenation of the strings s1, s2,…
- DOLLAR — num formatted as currency
- EXACT — TRUE if string1 is exactly equal to string2
- FIND — first position of string1 in string2 following position start
- FINDB — first byte position of string1 in string2 following byte position start
- FIXED — formatted string representation of num
- JIS — text with half-width katakana and ASCII characters converted to full-width
- LEFT — the first num_chars characters of the string s
- LEFTB — the first characters of the string s comprising at most num_bytes bytes
- LEN — the number of characters of the string s
- LENB — the number of bytes in the string s
- LOWER — a lower-case version of the string text
- MID — the substring of the string s starting at position position consisting of length characters
- MIDB — the characters following the first start_pos bytes comprising at most num_bytes bytes
- NUMBERVALUE — numeric value of text
- PROPER — text with initial of each word capitalised
- REPLACE — string old with num characters starting at start replaced by new
- REPLACEB — string old with up to num bytes starting at start replaced by new
- REPT — num repetitions of string text
- RIGHT — the last num_chars characters of the string s
- RIGHTB — the last characters of the string s comprising at most num_bytes bytes
- SEARCH — the location of the search string within text after position start
- SEARCHB — the location of the search string within text after byte position start
- SUBSTITUTE — text with all occurrences of old replaced by new
- T — value if and only if value is text, otherwise empty
- TEXT — value as a string formatted as format
- TEXTJOIN — the concatenation of the strings s1, s2,… delimited by del
- TRIM — text with only single spaces between words
- UNICHAR — the Unicode character represented by the Unicode code point x
- UNICODE — the Unicode code point for the character c
- UPPER — an upper-case version of the string text
- VALUE — numeric value of text
ASC
Synopsis
ASC(text)
Arguments
text: string
Description
ASC converts full-width katakana and ASCII characters to half-width equivalent characters, copying all others.
The distinction between half-width and full-width characters is described in http://www.unicode.org/reports/tr11/.
Note
While in obsolete encodings ASC used to translate between 2-byte and 1-byte characters, this is not the case in UTF-8.
Microsoft Excel Compatibility
For most strings, this function has the same effect as in Excel.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
JIS.
CHAR
Synopsis
CHAR(x)
Arguments
x: code point
Description
CHAR(x) returns the CP1252 (Windows-1252) character with code x.
x must be in the range 1 to 255.
CP1252 (Windows-1252) is also known as the "ANSI code page", but it is not an ANSI standard.
CP1252 (Windows-1252) is based on an early draft of ISO-8859-1, and contains all of its printable characters. It also contains all of ISO-8859-15's printable characters (but partially at different positions.)
This function is Excel compatible.
Note
In CP1252 (Windows-1252), 129, 141, 143, 144, and 157 do not have matching characters. For x from 1 to 255 except 129, 141, 143, 144, and 157 we have CODE(CHAR(x))=x.
See also
CODE.
CLEAN
Synopsis
CLEAN(text)
Arguments
text: string
Description
CLEAN removes non-printable characters from its argument leaving only regular characters and white-space.
Microsoft Excel Compatibility
This function is Excel compatible.
CODE
Synopsis
CODE(c)
Arguments
c: character
Description
c must be a valid CP1252 (Windows-1252) character.
CP1252 (Windows-1252) is also known as the "ANSI code page", but it is not an ANSI standard.
CP1252 (Windows-1252) is based on an early draft of ISO-8859-1, and contains all of its printable characters (but partially at different positions.)
This function is Excel compatible.
Note
In CP1252 (Windows-1252), 129, 141, 143, 144, and 157 do not have matching characters. For x from 1 to 255 except 129, 141, 143, 144, and 157 we have CODE(CHAR(x))=x.
See also
CHAR.
CONCAT
Synopsis
CONCAT(s1,s2,…)
Arguments
s1: first string
s2: second string
Note
This function is identical to CONCATENATE
Microsoft Excel Compatibility
This function is Excel compatible.
CONCATENATE
Synopsis
CONCATENATE(s1,s2,…)
Arguments
s1: first string
s2: second string
Microsoft Excel Compatibility
This function is Excel compatible.
DOLLAR
Synopsis
DOLLAR(num,decimals)
Arguments
num: number
decimals: decimals
Microsoft Excel Compatibility
This function is Excel compatible.
EXACT
Synopsis
EXACT(string1,string2)
Arguments
string1: first string
string2: second string
Microsoft Excel Compatibility
This function is Excel compatible.
FIND
Synopsis
FIND(string1,string2,start)
Arguments
string1: search string
string2: search field
start: starting position, defaults to 1
Note
This search is case-sensitive.
Microsoft Excel Compatibility
This function is Excel compatible.
FINDB
Synopsis
FINDB(string1,string2,start)
Arguments
string1: search string
string2: search field
start: starting byte position, defaults to 1
Note
This search is case-sensitive.
Microsoft Excel Compatibility
While this function is syntactically Excel compatible, the differences in the underlying text encoding will usually yield different results.
OpenDocument Format (ODF) Compatibility
While this function is OpenFormula compatible, most of its behavior is, at this time, implementation specific.
FIXED
Synopsis
FIXED(num,decimals,no_commas)
Arguments
num: number
decimals: number of decimals
no_commas: TRUE if no thousand separators should be used, defaults to FALSE
Microsoft Excel Compatibility
This function is Excel compatible.
JIS
Synopsis
JIS(text)
Arguments
text: original text
Description
JIS converts half-width katakana and ASCII characters to full-width equivalent characters, copying all others.
The distinction between half-width and full-width characters is described in http://www.unicode.org/reports/tr11/.
Note
While in obsolete encodings JIS used to translate between 1-byte and 2-byte characters, this is not the case in UTF-8.
Microsoft Excel Compatibility
For most strings, this function has the same effect as in Excel.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
ASC.
LEFT
Synopsis
LEFT(s,num_chars)
Arguments
s: the string
num_chars: the number of characters to return (defaults to 1)
Note
If the string s is in a right-to-left script, the returned first characters are from the right of the string.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
LEFTB
Synopsis
LEFTB(s,num_bytes)
Arguments
s: the string
num_bytes: the maximum number of bytes to return (defaults to 1)
Note
The semantics of this function is subject to change as various applications implement it. If the string is in a right-to-left script, the returned first characters are from the right of the string.
Microsoft Excel Compatibility
While this function is syntactically Excel compatible, the differences in the underlying text encoding will usually yield different results.
OpenDocument Format (ODF) Compatibility
While this function is OpenFormula compatible, most of its behavior is, at this time, implementation specific.
LEN
Synopsis
LEN(s)
Arguments
s: the string
Microsoft Excel Compatibility
This function is Excel compatible.
LENB
Synopsis
LENB(s)
Arguments
s: the string
Microsoft Excel Compatibility
This function is Excel compatible.
LOWER
Synopsis
LOWER(text)
Arguments
text: string
Microsoft Excel Compatibility
This function is Excel compatible.
See also
MID
Synopsis
MID(s,position,length)
Arguments
s: the string
position: the starting position
length: the number of characters to return
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
MIDB
Synopsis
MIDB(s,start_pos,num_bytes)
Arguments
s: the string
start_pos: the number of the byte with which to start (defaults to 1)
num_bytes: the maximum number of bytes to return (defaults to 1)
Note
The semantics of this function is subject to change as various applications implement it.
Microsoft Excel Compatibility
While this function is syntactically Excel compatible, the differences in the underlying text encoding will usually yield different results.
OpenDocument Format (ODF) Compatibility
While this function is OpenFormula compatible, most of its behavior is, at this time, implementation specific.
NUMBERVALUE
Synopsis
NUMBERVALUE(text,separator)
Arguments
text: string
separator: decimal separator
Note
If text does not look like a decimal number, NUMBERVALUE returns the value VALUE would return (ignoring the given separator).
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
See also
PROPER
Synopsis
PROPER(text)
Arguments
text: string
Microsoft Excel Compatibility
This function is Excel compatible.
REPLACE
Synopsis
REPLACE(old,start,num,new)
Arguments
old: original text
start: starting position
num: number of characters to be replaced
new: replacement string
Microsoft Excel Compatibility
This function is Excel compatible.
See also
MID, SEARCH, SUBSTITUTE, TRIM.
REPLACEB
Synopsis
REPLACEB(old,start,num,new)
Arguments
old: original text
start: starting byte position
num: number of bytes to be replaced
new: replacement string
Description
REPLACEB replaces the string of valid unicode characters starting at the byte start and ending at start+num-1 with the string new.
Note
The semantics of this function is subject to change as various applications implement it.
Microsoft Excel Compatibility
While this function is syntactically Excel compatible, the differences in the underlying text encoding will usually yield different results.
OpenDocument Format (ODF) Compatibility
While this function is OpenFormula compatible, most of its behavior is, at this time, implementation specific.
See also
MID, SEARCH, SUBSTITUTE, TRIM.
REPT
Synopsis
REPT(text,num)
Arguments
text: string
num: non-negative integer
Microsoft Excel Compatibility
This function is Excel compatible.
See also
RIGHT
Synopsis
RIGHT(s,num_chars)
Arguments
s: the string
num_chars: the number of characters to return (defaults to 1)
Note
If the string s is in a right-to-left script, the returned last characters are from the left of the string.
Microsoft Excel Compatibility
This function is Excel compatible.
OpenDocument Format (ODF) Compatibility
This function is OpenFormula compatible.
RIGHTB
Synopsis
RIGHTB(s,num_bytes)
Arguments
s: the string
num_bytes: the maximum number of bytes to return (defaults to 1)
Note
The semantics of this function is subject to change as various applications implement it. If the string s is in a right-to-left script, the returned last characters are from the left of the string.
Microsoft Excel Compatibility
While this function is syntactically Excel compatible, the differences in the underlying text encoding will usually yield different results.
OpenDocument Format (ODF) Compatibility
While this function is OpenFormula compatible, most of its behavior is, at this time, implementation specific.
SEARCH
Synopsis
SEARCH(search,text,start)
Arguments
search: search string
text: search field
start: starting position, defaults to 1
Description
search may contain wildcard characters (*) and question marks (?). A question mark matches any single character, and a wildcard matches any string including the empty string. To search for * or ?, precede the symbol with ~.
Note
This search is not case sensitive. If search is not found, SEARCH returns #VALUE! If start is less than one or it is greater than the length of text, SEARCH returns #VALUE!
Microsoft Excel Compatibility
This function is Excel compatible.
SEARCHB
Synopsis
SEARCHB(search,text,start)
Arguments
search: search string
text: search field
start: starting byte position, defaults to 1
Description
search may contain wildcard characters (*) and question marks (?). A question mark matches any single character, and a wildcard matches any string including the empty string. To search for * or ?, precede the symbol with ~.
Note
This search is not case sensitive. If search is not found, SEARCHB returns #VALUE! If start is less than one or it is greater than the byte length of text, SEARCHB returns #VALUE! The semantics of this function is subject to change as various applications implement it.
Microsoft Excel Compatibility
While this function is syntactically Excel compatible, the differences in the underlying text encoding will usually yield different results.
OpenDocument Format (ODF) Compatibility
While this function is OpenFormula compatible, most of its behavior is, at this time, implementation specific.
SUBSTITUTE
Synopsis
SUBSTITUTE(text,old,new,num)
Arguments
text: original text
old: string to be replaced
new: replacement string
num: if num is specified and a number only the numth occurrence of old is replaced
Microsoft Excel Compatibility
This function is Excel compatible.
T
Synopsis
T(value)
Arguments
value: original value
Microsoft Excel Compatibility
This function is Excel compatible.
TEXT
Synopsis
TEXT(value,format)
Arguments
value: value to be formatted
format: desired format
Microsoft Excel Compatibility
This function is Excel compatible.
TEXTJOIN
Synopsis
TEXTJOIN(del,blank,s1,s2,…)
Arguments
del: delimiter
blank: ignore blanks
s1: first string
s2: second string
Microsoft Excel Compatibility
This function is Excel compatible.
See also
TRIM
Synopsis
TRIM(text)
Arguments
text: string
Microsoft Excel Compatibility
This function is Excel compatible.
See also
CLEAN, MID, REPLACE, SUBSTITUTE.
UNICHAR
Synopsis
UNICHAR(x)
Arguments
x: Unicode code point
UNICODE
Synopsis
UNICODE(c)
Arguments
c: character
A.17. Time Series Analysis
- FOURIER — Fourier or inverse Fourier transform
- HPFILTER — Hodrick Prescott Filter
- INTERPOLATION — interpolated values corresponding to the given abscissa targets
- PERIODOGRAM — periodogram of the given data
FOURIER
Synopsis
FOURIER(Sequence,Inverse,Separate)
Arguments
Sequence: the data sequence to be transformed
Inverse: if true, the inverse Fourier transform is calculated, defaults to false
Separate: if true, the real and imaginary parts are given separately, defaults to false
Description
This array function returns the Fourier or inverse Fourier transform of the given data sequence.
The output consists of one column of complex numbers if Separate is false and of two columns of real numbers if Separate is true.
If Separate is true the first output column contains the real parts and the second column the imaginary parts.
Note
If Sequence is neither an n by 1 nor 1 by n array, this function returns #VALUE!
HPFILTER
Synopsis
HPFILTER(Sequence,λ)
Arguments
Sequence: the data sequence to be transformed
λ: filter parameter λ, defaults to 1600
Description
This array function returns the trend and cyclical components obtained by applying the Hodrick Prescott Filter with parameter λ to the given data sequence.
The output consists of two columns of numbers, the first containing the trend component, the second the cyclical component.
Note
If Sequence is neither an n by 1 nor 1 by n array, this function returns #VALUE! If Sequence contains less than 6 numerical values, this function returns #VALUE!
INTERPOLATION
Synopsis
INTERPOLATION(abscissae,ordinates,targets,interpolation)
Arguments
abscissae: abscissae of the given data points
ordinates: ordinates of the given data points
targets: abscissae of the interpolated data
interpolation: method of interpolation, defaults to 0 ('linear')
Description
The output consists always of one column of numbers.
Possible interpolation methods are:
0: linear;
1: linear with averaging;
2: staircase;
3: staircase with averaging;
4: natural cubic spline;
5: natural cubic spline with averaging.
Note
The abscissae should be given in increasing order. If the abscissae is not in increasing order the INTERPOLATION function is significantly slower. If any two abscissae values are equal an error is returned. If any of interpolation methods 1 ('linear with averaging'), 3 ('staircase with averaging'), and 5 ('natural cubic spline with averaging') is used, the number of returned values is one less than the number of targets and the target values must be given in increasing order. The values returned are the average heights of the interpolation function on the intervals determined by consecutive target values. Strings and empty cells in abscissae and ordinates are ignored. If several target data are provided they must be in the same column in consecutive cells.
See also
PERIODOGRAM
Synopsis
PERIODOGRAM(ordinates,filter,abscissae,interpolation,number)
Arguments
ordinates: ordinates of the given data
filter: windowing function to be used, defaults to no filter
abscissae: abscissae of the given data, defaults to regularly spaced abscissae
interpolation: method of interpolation, defaults to none
number: number of interpolated data points
Description
If an interpolation method is used, the number of returned values is one less than the number of targets and the targets values must be given in increasing order.
The output consists always of one column of numbers.
Possible interpolation methods are:
0: linear;
1: linear with averaging;
2: staircase;
3: staircase with averaging;
4: natural cubic spline;
5: natural cubic spline with averaging.
Possible window functions are:
0: no filter (rectangular window)
1: Bartlett (triangular window)
2: Hahn (cosine window)
3: Welch (parabolic window)
Note
Strings and empty cells in abscissae and ordinates are ignored. If several target data are provided they must be in the same column in consecutive cells.
See also
B. Keybinding Reference
This appendix lists the keyboard shortcuts which are defined by default in Gnumeric.
Keybindings are combinations of keystrokes which tell an application to run a task. These can greatly speed-up the user's interactions with an application. Some of the most common ones are Ctrl+s to save a file or Ctrl+q to quit the application. Gnumeric also comes with keybindings to make your spreadsheet experience faster.
Normally, keybindings are next to a command in a menu. For example, if has Ctrl+s next to it, that means that Ctrl+s can be typed at the same time to save your file. However, some keystrokes aren't listed in the menus. They are as follows:
- F2 sets the current cell for editing. The cursor is inserted at the end of the current text.
- Ctrl-O opens the Load file dialog window.
- Ctrl-F3 opens the Define Name dialog window.
- F4 repeat the last action.
- Ctrl-G opens the Go to dialog window which allows you to jump to a specified cell.
- Ctrl-H opens the Search and Replace dialog where you can search through your spreadsheets for text strings and replace them with something else.
- Ctrl-F opens the Search Center. The Search Center allows you to search through your spreadsheets for text strings.
- Ctrl-~ Formats the current selection as a 'General'.
- Ctrl-$ Formats the current selection with the default currency
- Ctrl-# Formats the current selection with default date style
- Ctrl-^ Formats the current selection as superscript
- Ctrl-@ Formats the current selection with the default time format
- Ctrl-! Formats the current selection as an integer (a number with no decimal places).
- Ctrl-& Adds a thin border around the current selection
- Ctrl-_ Formats the current selection as subscript
- Ctrl-$ Formats the current selection as the default currency
- Ctrl-B or Ctrl-2 Toggles the boldness of the font in the current selection.
- Ctrl-I or Ctrl-3 Toggles the italics of the font in the current selection.
- Ctrl-U or Ctrl-4 Toggles single underlining of the current selection.
- Ctrl-5 Toggles strikethrough of the current selection.
- Shift-Ctrl-G Changes the keyboard focus to the current cell indicator described in Section 4.5.1 ― Current Cell Indicator.
- Ctrl-a Select all cells on the currently focused sheet.
For the sake of compatibility with Excel, Gnumeric also assigns a serial number to February 29th, 1900 as if 1900 had been a leap year even though it was not. So February 28th, 1900 has the serial number 59 and March 1st, 1900 the serial number 61. If you try to format the serial number 60 as a date, Gnumeric recognizes that that date does not exist and shows a sequence of # symbols.
Gnumeric random numbers are generated using the Mersenne twister MT19937 pseudo-random number generator as implemented in the GNU Scientific Library.
Adapted from Banks, Carson, Nelson and Nicol (2001), Discrete-Event System Simulation, 3rd ed. pp. 42-45.